Entier quadratique - Définition
La liste des auteurs de cet article est disponible ici.
Caractérisation
Irrationnel quadratique
L'un des objets de l'article est l'étude des nombres répondant à la définition suivante :
Il existe une manière simple de caractériser les nombres quadratiques :
-
- Un nombre α est irrationnel quadratique si, et seulement si, il existe deux rationnels a et b, tel que b soit non nul, et un entier sans facteur carré d tel que α est égal à a + b.√d.
Il existe une convention prise ici, que les analystes ne font pas. Il n'est dit nul part que d est un entier positif, ce qui sous-entend que l'expression √d peut décrire la racine carrée d'un nombre négatif. En analyse, cette situation est dangereuse, on ne sait pas si cette racine désigne i.√-d ou -i.√-d et il n'est pas possible d'adopter une convention qui rende la fonction racine continue sur l'ensemble des nombres complexes. Le paragraphe suivant montre que cette difficulté n'existe pas dans le contexte de cet article. Pour une raison de commodité, l'usage du radical racine pour des entiers négatifs est fréquent en théorie algébrique des nombres, cette convention est utilisée ici.
Si α est solution d'une équation du second degré à coefficients rationnels alors la technique de résolution de cette équation à l'aide d'un discriminant montre qu'il existe trois rationnels a, c et e tel que α = a + c.√e. Si e est une fraction dont un représentant est f / g, quitte à multiplier en haut et en bas de la fraction par les facteurs non carrés du dénominateur, il est possible d'écrire e sous la forme d'un entier divisé par un carré parfait. Il est alors possible de sortir le dénominateur du radical. On peut donc choisir e entier. Si e contient des facteurs carrés, il est encore possible de les sortir du radical, on obtient alors une expression de la forme a + b.√d, où a et b sont des nombres rationnels et d un entier sans carré parfait. Comme le nombre α n'est pas choisi rationnel, le coefficient b n'est pas nul.
Réciproquement si α est égal à a + b.√d, il est solution de l'équation suivante :
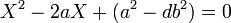
Corps quadratique
Le nombre d désigne dans le reste de l'article un entier sans facteur carré, la lettre Z désigne l'anneau des nombres entiers, Q le corps des rationnels, R celui des réels et C celui des complexes.
L'intérêt de la notion de nombre quadratique provient de structures algébriques sous-jacentes à ce nombre. On étudie plus les propriétés des structures associées que le nombre lui-même. Une des structures essentiels correspond au plus petit ensemble contenant l'irrationnel quadratique, contenant 1 et stable par addition, soustraction, multiplication et division. Évidemment, cette stabilité ne concerne pas la division par 0.
L'ensemble des nombres de la forme x + y.√d est généralement noté Q[√d], les résultats précédents s'expriment, en terme mathématiques, par le fait que Q[√d] dispose d'une structure de corps.
-
- Un corps quadratique K est un sous-corps du corps des complexes tel qu'il existe un entier sans facteur carré d et K est égal à Q[√d]. Un élément de ce corps est appelé nombre quadratique.
Ainsi les définitions de nombre quadratique et irrationnel quadratique sont très similaires. Tout irrationnel quadratique est un nombre quadratique, réciproquement, un nombre quadratique non rationnel est un irrationnel quadratique. On peut imaginer définir un corps quadratique différemment, comme un corps ne contenant que des nombres quadratiques. La proposition suivante montre qu'une telle démarche est licite.
-
- Soit un corps commutatif K contenant Q mais non restreint à Q et qui ne contienne que des nombres quadratiques. Il existe un entier d, sans facteur carré, tel que K soit isomorphe à Q[√d].
Les algébristes construisent souvent le corps K d'une autre manière. Ils considèrent tout d'abord l'anneau des polynômes à coefficients dans les rationnels. Comme l'ensemble Q des rationnels est un corps, cet anneau est euclidien. Le polynôme X2 - d est irréductible si d est un entier sans facteur carré. Irréductible signifie qu'il ne peut pas s'exprimer comme un produit de deux polynômes de degré 1. L'Idéal engendré par X2 - d est un idéal maximal car l'anneau des polynômes est euclidien, donc principal, et le quotient de l'anneau des polynômes par cet idéal maximal est un corps. Tout élément de ce corps s'écrit x + y.√d si √d désigne la classe du polynôme X. Le signe de d ne modifie en rien la validité de la construction. Comme X2 - d est dans l'ideal quotient, la classe de X possède un carré égal à d, qu'il soit positif ou négatif, ce qui justifie la notation. Elle est d'autant plus cohérente que ce corps est une copie, le terme exact est isomorphe, du plus petit sous-corps de C contenant √d ou i.√-d si d est négatif.
-
- Le plus petit sous-corps contenant le nombre quadratique a + b.√d est K[d] :
Comme cet ensemble est stable par addition et soustraction et contient 1, il contient tous les entiers. Comme il est stable par division, il contient tous les rationnels. Par hypothèse il contient le nombre quadratique a + b.√d, en additionnant -a, on remarque qu'il contient b.√d et en divisant par b, il contient aussi √d. Il contient donc 1 et √d, et nécessairement tous les nombres de la forme x + y.√d, où x et y décrivent l'ensemble des rationnels.
Réciproquement, l'ensemble des nombres de la forme x + y.√d contient 1 et a + b.√d. Il est stable pour les quatre opérations. La stabilité de l'addition et de la soustraction est évidente, celle de la multiplication provient de la propriété suivante :
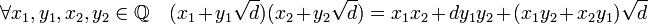
Il faut encore vérifier que tout élément non nul admet bien un inverse dans cet ensemble. On remarque tout d'abord que x2 - d.y2 ne peut être nul. S'il l'était alors d serait un quotient de carrés parfaits or d est un entier sans facteur carré. Il suffit alors de remarquer que si x et y est un couple de rationnels non tous les deux nuls :
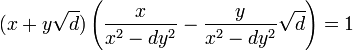
-
- Soit un corps commutatif K contenant Q mais non restreint à Q qui ne contiennent que des nombres quadratiques. Il existe un entier d, sans facteur carré, tel que K soit isomorphe à Q[√d] :
La théorie de Galois permet de résoudre cette question très simplement en faisant appel au théorème de l'élément primitif. Il suffit de considérer n'importe qu'elle extension finie de Q dans K, elle admet un élément primitif, elle est donc de degré 2. Le corps K n'admet que des sous-corps de degré 2 sur Q, il est donc de degré 2.
Il est néanmoins possible de démontrer sans outil puissant ce petit résultat. Nous savons a priori quatre choses sur le corps K : qu'il est commutatif, de caractéristique nulle et que tout élément est racine d'un polynôme de degré inférieur ou égal à 2 à coefficients dans son corps caractéristique et qu'il contient un élément qui n'est pas dans le corps caractéristique.
La caractéristique d'un corps est égal au plus petit entier n, tel que 1, additionné n fois à lui-même soit égal à 0. Si un tel n n'existe pas, le corps est qualifié de caractéristique nulle. Le corps caractéristique est le plus petit sous-corps de K. Il contient nécessairement 1 et donc le sous corps engendré par 1. Si le corps est de caractéristique nulle, il contient une copie de Z et nécessairement une copie de Q. On identifie en général cette copie avec Q ce que nous faisons ici.
Dans le cas présent, il existe un élément α qui n'est pas dans Q, cet élément est racine d'un polynôme de degré 2, à coefficients dans Q et irréductible. Il est donc de la forme a + √d.b où a et b sont des rationnels et √d un nombre tel que son carré est égal à d, un élément de Q. La même approche que celle utilisée précédemment montre que d peut être choisi entier sans facteur carré. Soit α1 un élément quelconque de K, l'objectif est de montrer qu'il existe deux rationnels a1 et b1 tel que α1 = a1 + b1.√d.
Si α1 est rationnel l'objectif est immédiatement atteint. Supposons qu'il ne le soit pas. Le même raisonnement que précédemment montre que α1 = a1 + b1.√f où f est encore un entier sans facteur carré. Il suffit donc de montrer que f est égal à d. Pour cela remarquons que √d et √f sont deux éléments de K leur somme est encore élément de K, donc solution d'une équation du second degré à coefficients dans Q.
Soit P[X] = X2 + hX + k un polynôme à coefficients dans Q et ayant √d + √f comme racine. On dispose de l'égalité suivante :
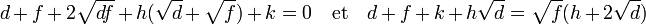
On remarque que h + 2√d ne peut être nul car √d n'est pas rationnel alors que h l'est. On en déduit que √f est le quotient de deux éléments de Q[√d], ce qui montre qu'il est élément de Q[√d] et :
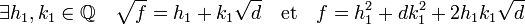
Ceci montre qu'un rationnel multiplié par √d est un rationnel. Le seul rationnel ayant cette propriété est 0, et soit h1 soit k1 est nul. Si k1 est nul, √f est rationnel, ce qui est contraire aux hypothèses, donc h1 est nul et √f = k1√d, et f est égal à k12.d. Or f est un entier sans facteur carré, donc k1 est égal à 1 et f à d.
Il est temps de conclure. K contient Q[√d] car c'est un corps contenant √d. Réciproquement tout élément de K est contenu dans Q[√d] d'après l'analyse précédente. Les deux structures sont bien égales.
Entier quadratique
Un des charmes d'un corps quadratique, général à tout corps algébrique, est qu'il présente une structure un peu analogue à celle des nombres rationnels. Tout comme les nombres rationnels disposent d'entiers, un corps quadratique dispose aussi d'entiers, la définition peut néanmoins paraître un peu étrange en premier abord, la suite montre qu'elle est parfaitement justifiée :
-
- Un entier quadratique est un élément d'un corps quadratique dont le polynôme minimal est à coefficients dans Z.
Le polynôme minimal d'un nombre α est le polynôme à coefficients rationnels de plus petit degré, de monôme dominant ayant un coefficient égal à 1 et ayant α pour racine. L'article sur ce concept montre qu'il est unique et tout polynôme à coefficients rationnels ayant α pour racine est un multiple du polynôme minimal. Un irrationnel quadratique possède un polynôme minimal nécessairement de degré 2, un entier algébrique peut aussi être rationnel et posséder un polynôme minimal de degré 1, cette différence subtile, permet de considérer un élément de Z comme un entier quadratique. Il serait étrange de considérer 1 comme non entier et 1/2 comme un irrationnel quadratique, d'où la différence dans la définition.
L'article entier algébrique correspondant à la généralisation du concept pour un corps algébrique quelconque montre que les seuls entiers algébriques de Q sont les éléments de Z. L'analogie va plus loin :
-
- La somme, la différence et le produit de deux entiers algébriques est un entier algébrique.
Cette situation est encore comparable à celle de Z. On peut encore dire que l'ensemble des entiers algébriques d'un corps quadratique forme un anneau. Cette situation est la même pour tous les corps algébriques, d'où une définition générale :
-
- L' anneau des entiers d'un corps algébrique K est appelé fermeture intégrale de Z dans K et est souvent noté OK.
Il est intéressant de caractériser l'ensemble des entiers algébriques d'un corps quadratique :
-
- Si d est congru à 1 modulo 4, alors l'anneau des entiers algébrique de Q[√d] est égal à Z[(1 + √d) / 2], sinon l'anneau est égal à Z[√d].
L'expression, Z[ω] désigne l'ensemble des nombres de la forme a0 + a1.ω + a2.ω2 + ... + an.ωn, où a0, a1, ..., an sont des éléments de Z. Ici, ω2 s'écrit toujours comme une combinaison linéaire à coefficients dans Z de 1 et de ω, elle est donnée par le polynôme minimal, si ω désigne une des valeurs de l'énoncé de la proposition, à savoir (1 + √d) / 2 ou bien √d. Dans toute la suite de l'article ω désigne cette valeur. Un élément de l'anneau Z[ω] est donc de la forme a + ω.b, où a et b sont des éléments de Z.
-
- Supposons que d ne soit pas congru à 1 modulo 4 :
Soit a et b deux entiers relatifs et v = a + b.√d, alors v est racine du polynôme P[X] suivant et est donc algébrique :
![P[X] = X^2 - 2a.X + a^2 - d.b^2\;](https://static.techno-science.net/illustration/Definitions/autres/0/04acc20d366ac5b6d5d97f8a101b861d_54a3293efb5f91794483b3d08bd7d35e.png)
Réciproquement, supposons w algébrique, il existe deux rationnels α et β tel que w = α + β.√d et si le polynôme minimal de w est noté Q[X] alors :
![Q[X] = X^2 - 2\alpha.X + \alpha^2 - d.\beta^2\quad \text{et}\quad 2\alpha \in \mathbb Z\; ,\quad \alpha^2 - d.\beta^2 \in \mathbb Z\;](https://static.techno-science.net/illustration/Definitions/autres/7/75191f8a5f076bec3dabbc15e027d19b_535ebe1e6bf8349270715e826d0f52b2.png)
les nombres 2.α et 4(α2 - d.β2) sont des entiers relatifs et 4.d.β2 l'est aussi. Comme d ne contient aucun facteur carré, 2.β est un entier relatif.
Si d est congru à 2 modulo 4, alors 2.d.β2 est élément de Z et 2.α2 aussi, comme 2.α est un entier relatif, α l'est aussi. On en déduit que d.β2 est un entier relatif, comme d n'est pas un multiple de 4, et que 2.β est un entier relatif, β l'est aussi.
Si d est congru à 3 modulo 4, (2.α)2 - d.(2.β)2) est un multiple de 4, si (2.β) est impair, alors (2.β)2 est congru à 1 modulo 4, d.(2.β)2 est congru à 3 modulo 4 et (2.α)2 - d.(2.β)2) est congru à 2 modulo 4, ce qui est impossible, c'est un multiple de quatre. On en déduit que 2.β est pair et β est entier. Ceci montre que d.(2.β)2 est un multiple de 4, et donc (2.α)2 aussi, on en déduit que α est entier.
-
- Supposons que d soit congru à 1 modulo 4 :
Soit a et b deux entiers relatifs et v = a + b(1 + √d)/2, alors v est racine du polynôme P[X] suivant et est donc entier algébrique car d - 1 est un multiple de quatre :
![P[X] = X^2 - (2a+b).X + a^2 + a.b - b^2\frac{d-1}4\;](https://static.techno-science.net/illustration/Definitions/autres/c/c64771c2b7f9595a60195a83f525ee56_fcebb3947f9f1ba2966d926495fdd386.png)
Réciproquement, supposons w algébrique, il existe deux rationnels α et β tel que w = α + β.(1 + √d)/2 et si le polynôme minimal de w est noté Q[X] alors :
![Q[X] = X^2 - (2\alpha + \beta).X + \alpha^2 + \alpha.\beta - \beta^2\frac{d-1}4\quad \text{et}\quad 2\alpha + \beta \in \mathbb Z\; ,\quad (\alpha + \frac\beta 2)^2 - \beta^2\frac d4 \in \mathbb Z\;](https://static.techno-science.net/illustration/Definitions/autres/8/89563166aa7dfc9f82b64ee7e31dc500_5748c9c27d8f4a3233bef9445b3a184b.png)
On en déduit que (2α + β)2 - d.β2 est un multiple de 4, comme 2α + β est un entier relatif, d.β2 l'est aussi. Comme d ne contient aucun facteur carré, β est un entier relatif. Comme (2α + β)2 - d.β2 est un multiple de quatre et que β est un entier relatif, 4(α2 + α.β) est un multiple de 4 (car d - 1 est un multiple de quatre) et (2α)2 + 2.(2.α).β est un multiple de 4. Comme 2α + β et β sont des entiers relatifs, 2α l'est aussi. Si 2α est impair, alors (2α)2 + 2.(2.α).β est impair, or cette valeur est un multiple de 4, donc α est un entier relatif, ce qui termine la démonstration.
-
- La fermeture intégrale de Z dans un corps quadratique est un anneau :
L'ensemble considéré est manifestement un groupe abélien, il suffit donc de montrer la stabilité pour la multiplication, les autres propriétés se déduisent du fait que la fermeture intégrale est une partie d'un corps. Soit d un entier relatif sans facteur carré, les deux égalités suivantes montrent que dans tous les cas, la fermeture est stable par multiplication :
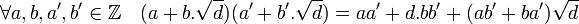
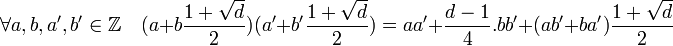
Fermeture intégrale et clôture intégrale
La configuration est celle du corps, ici un corps quadratique, contenant un anneau, celui des entiers quadratiques. Elle ressemble un peu à celle de Q et Z à cet égard. La relation entre Z et Q est aussi caractérisée par le fait que Q est le corps des fractions de Z, c'est-à-dire le plus petit corps contenant Z. En fait, Q est construit comme l'ensemble des couples (a, b); où a est un entier et b un entier non nul, quotienté par une relation d'équivalence. On peut appliquer la même méthode à l'anneau des entiers d'un corps quadratique pour rechercher le plus petit corps contenant cet anneau.
-
- Le corps des fractions de l'anneau des entiers d'un corps quadratique Q[√d] est isomorphe à Q[√d].
Pour cette raison le terme de rationnel quadratique désigne un élément de ce corps. Un rationnel quadratique est un nombre quadratique, il correspond soit à un irrationnel quadratique, soit à un élément de Q. Comme précédemment, on peut se poser la question de la forme d'un anneau unitaire (c'est-à-dire qui contient l'élément 1) composé uniquement d'entiers quadratiques. La situation est un peu différente que celle de Q et Z, ici il existe d'autres anneaux, toujours inclus dans une fermeture intégrale :
-
- Soit A un anneau unitaire contenant strictement Z et formé uniquement d'entiers quadratiques. Il existe un entier d, non carré parfait, tel que A est égal à Z[ω] ou ω est égal soit à √d soit, si d est congru à 1 modulo 4, à (1 + √d) / 2.
La nuance provient de la nature de d. Dans une fermeture intégrale d est un entier sans facteur carré, comme 2 ou -6. Dans la proposition précédente d est un entier non carré parfait comme 18 ou -12. Or 18 et -12 ne sont pas des entiers sans facteur carré. Ainsi le corps Q'[√3] contient l'anneau Z[√3] mais aussi Z[√12]. Cette différence donne lieu à la définition suivante :
-
- Un anneau d'entiers quadratiques est dit intégralement clos si et seulement s'il est égal à sa clôture intégrale.
Le corps des fractions de Z[√12] contient √3 et est en fait égal à Q[√3]. L'anneau des entiers de Q[√3] est égal à Z[√3] qui contient strictement Z[√12], qui n'est ainsi pas intégralement clos. Les anneaux intégralement clos sont les plus riches en propriétés. Par contre, Z[√-3] n'est pas un anneau euclidien, ni même factoriel. Pour s'en rendre compte, il suffit de considérer la double décomposition suivante du nombre 4 en facteurs irréductibles :
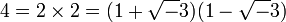
En revanche, l'anneau Z[1/2(1 +√-3)] composé des entiers d'Eisenstein est euclidien, comme le montre l'article sur la question.
Enfin, il existe une propriété fort utile sur les anneaux unitaires d'entiers quadratiques :
-
- l'intersection d'un anneau unitaire d'entiers quadratiques et de Q est égale à Z.
-
- Le corps des fractions de l'anneau des entiers d'un corps quadratique Q[√d] est isomorphe à Q[√d].
Le plus petit corps contenant les entiers quadratiques de Q[√d] contient 1 et √d, il contient nécessairement Q[√d]. Réciproquement Q[√d] contient tous les éléments de l'anneau des entiers, ce qui montre que Q[√d] est bien le plus petit corps contenant la fermeture intégrale. C'est donc, à un isomorphisme près, son corps des fractions.
-
- Soit A un anneau unitaire contenant strictement Z et formé uniquement d'entiers quadratiques. Il existe un entier f, non carré parfait, tel que A est égal à Z[ω] ou ω est égal soit à √f soit, si f est congru à 1 modulo 4, à (1 + √f) / 2.
On utilise pour cela le corps des fractions de A. Les démonstrations précédentes montrent que Q.A, c'est-à-dire l'ensemble des produits d'un rationnel par un élément de A est un corps, contenu dans son corps des fractions. Comme le corps des fractions est le plus petit contenant l'anneau, il est égal à Q.A. Ce qui montre l'existence d'un entier quadratique ω, de la forme de celle construite précédemment, tel que le corps des fractions de A soit égal à Q[ω]. Comme A est composé d'entiers quadratiques, A est un sous anneau de Z[ω] car Z[ω] contient tous les entiers quadratiques du corps. Il suffit de caractériser les sous-anneaux unitaires de Z[ω] pour démontrer cette proposition.
Supposons dans un premier temps qu'il existe un entier d sans facteur carré et non congru à 1 modulo 4 tel que ω soit égal à √d et considérons l'ensemble E de tous les entiers strictement positifs n tel que n.√d soit dans A. Montrons que cet ensemble est non vide, A n'est pas réduit à Z, il contient un élément de Z[ω] qui n'est pas un entier relatif. Soit a + b.√d un tel entier, avec a et b inclus dans Z et b non nul. Comme tous les entiers de A sont éléments de Z[ω], un élément de A possède nécessairement une forme de cette nature. Comme Z est inclus dans A, -a est élément de A et -a + a + b.√d = b.√d est aussi élément de A. Et |b| est élément de E. E est un ensemble non vide d'entiers strictement positifs, il possède donc un élément minimal m.
On définit f comme égal à m2.d. On remarque que √f est un élément de A puisque soit m√d soit -m√d l'est (si -m√d, alors m√d l'est aussi par stabilité de la soustraction). Par conséquence Z[√f] est inclus dans A. Montrons maintenant l'inclusion inverse. Soit a + b.√d un élément quelconque de Z, une fois encore b.√d est élément de A. considérons la division euclidienne de |b| par m, |b| = p.m + r. Comme |b|.√d et p.m.√d sont des éléments de A, par stabilité r.√d l'est aussi. Or r est strictement plus petit que m, le fait que r.√d soit élément de A montre que r est nul et b est un multiple de m. En conclusion a + b.√d est bien un élément de Z[√f]. On a montré que Z[√f] contient A et est contenu dans A, ils sont donc égaux.
Supposons maintenant que ω = 1/2(1 + √d) ou d est congru à 1 modulo 4. Le raisonnement précédent s'applique encore et il existe un entier strictement positif m tel que A soit égal à Z[m/2(1 + √d)]. Si m est paire, A est engengré par la somme d'un entier et de m√d que l'on note toujours f, ce qui montre que A est égal à Z[√f]. Supposons que m soit impair, alors A est engendré par (m - 1)/2 + 1/2(1 + √f) et donc par 1/2(1 + √f). Il ne reste plus qu'à monter que f est congru à 1 modulo 4. Dans ce dernier cas, m est impair, le carré de tout nombre impair est congru à 1 modulo 4, d l'est aussi, donc f égal à m2.d est congru à 1 modulo 4, ce qui termine la démonstration.
-
- l'intersection d'un anneau unitaire d'entiers quadratiques et de Q est égale à Z :
Dire que l'anneau est unitaire, signifie qu'il contient élément 1, par stabilité de l'addition et de la soustraction, il contient Z, réciproquement soit a un élément de l'intersection de l'anneau et de Q, comme il est élément de l'anneau, il est racine d'un polynôme de coefficient de monôme dominant égal à 1 et à coefficients dans Z. Ce polynôme admet pour racine a et son congugé est encore égal à a qui est donc une racine double, ont en déduit que son polynôme minimal est égal à X2 - 2a.X + a2. Ce qui montre que 2.a et a2 sont des éléments de Z. Dire que 2.a est élément de Z revient à dire qu'il existe un entier b tel que a est égal à b/2. Dire que b2/4 est entier signifie que b est un multiple de 2, ce qui montre que a est entier.