Entier algébrique - Définition
La liste des auteurs de cet article est disponible ici.
Structure
L'intérêt des entiers algébriques réside dans leur structure. Elle est à l'origine de démonstrations de nombreux théorèmes comme celui des unités de Dirichlet ou de la loi de réciprocité quadratique ou d'autres lois de réciprocité. Elle permet de résoudre des équations comme celles de Pell-Fermat ou de nombreux cas du dernier théorème de Fermat.
Anneau
Dans ce paragraphe A et B désigne deux anneaux commutatifs unitaires intègres et φ un morphisme de A dans B.
-
- Soit b1 et b2 deux éléments de B entiers sur A. Alors b1 - b2 et b1.b2 sont aussi entiers sur A.
Cette proposition, démontrée dans l'article détaillé, possède le corollaire suivant :
-
- La fermeture intégrale de A dans B est un anneau commutatif unitaire intègre.
En effet, la fermeture est non vide car elle contient φ(A), la proposition précédente montre que cette fermeture est un sous-anneau de B. En tant que sous-anneau de B, la fermeture est commutative et intègre, elle est unitaire car elle contient φ(A).
Propriétés noethériennes
La structure d'anneau est insuffisante pour démontrer de nombreux théorèmes. On cherche en conséquence à renforcer les propriétés des fermetures intégrales. Pour cela, il est nécessaire d'enrichir les structures de A et B. Une configuration importante est celle de la théorie de Galois. Une fermeture intégrale sur un corps de nombres peut être vu comme une extension de Z si l'extension est considérée sur Q ou comme une extension d'une fermeture intégrale d'un corps intermédiaire.
Dans ce paragraphe, on considère un anneau commutatif unitaire et intègre A. On suppose de plus que A est noethérien et on note K son corps des fractions. Soit L une extension finie de K que l'on suppose séparable. Si A est de caractéristique nulle l'extension L est toujours séparable, en effet le corps K est aussi de caractéristique nulle, il est donc parfait (c'est-à-dire que toute extension finie de K est séparable).
L'objectif est de déterminer des propriétés de la fermeture intégrale de A dans L. Il ne faut pas espérer trouver une structure d'anneau principal ou même factoriel, par exemple, la fermeture intégrale de Z dans Q[i√5] ne l'est pas (cf l'article Entier quadratique). À défaut d'être factoriel, une telle structure est noethérienne.
-
- La fermeture intégrale de A dans L est noethérienne en tant que A-module et en tant qu'anneau.
Une démonstration utilise la forme trace, une application bilinéaire définie sur le K espace vectoriel L. Comme l'extension est séparable, la forme trace est non dégénérée. Un isomorphisme entre la fermeture intégrale de A et le dual d'un A-module libre de type fini permet de conclure. Une démonstration est proposée dans l'article détaillé. Une autre fait usage des polynômes en plusieurs indéterminées, la démonstration est proposée dans l'article associé.
-
- La fermeture intégrale B de A dans L est intégralement close. Son corps des fractions est égal à L.
La première propriété résulte du fait que tout élément entier sur B est entier sur A. Tout élément α de L est algébrique sur K, un multiple de α par un élément
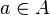
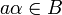
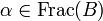
Anneau de Dedekind
L'anneau des entiers algébriques d'un corps de nombres K possède des propriétés supplémentaires. En plus d'être intégralement clos et de corps des fractions égal à K, ses idéaux premiers non-nuls sont maximaux. Un anneau noethérien intégralement clos possédant cette propriété sur ses idéaux premiers est appelé un anneau de Dedekind.
Il est clair que Z est un anneau commutatif unitaire intègre noethérien intégralement clos et que tout idéal premier non-nul de Z est maximal car Z est principal, c'est donc un anneau de Dedekind. Cette propriété se transporte à travers les extensions finies.
Si A est un anneau de Dedekind de corps des fractions K, L une extension finie, séparable de K et B la fermeture intégrale de A dans L, alors
-
- le corps des fractions de B est égal à L;
-
- l'anneau B est de Dedekind.

















































