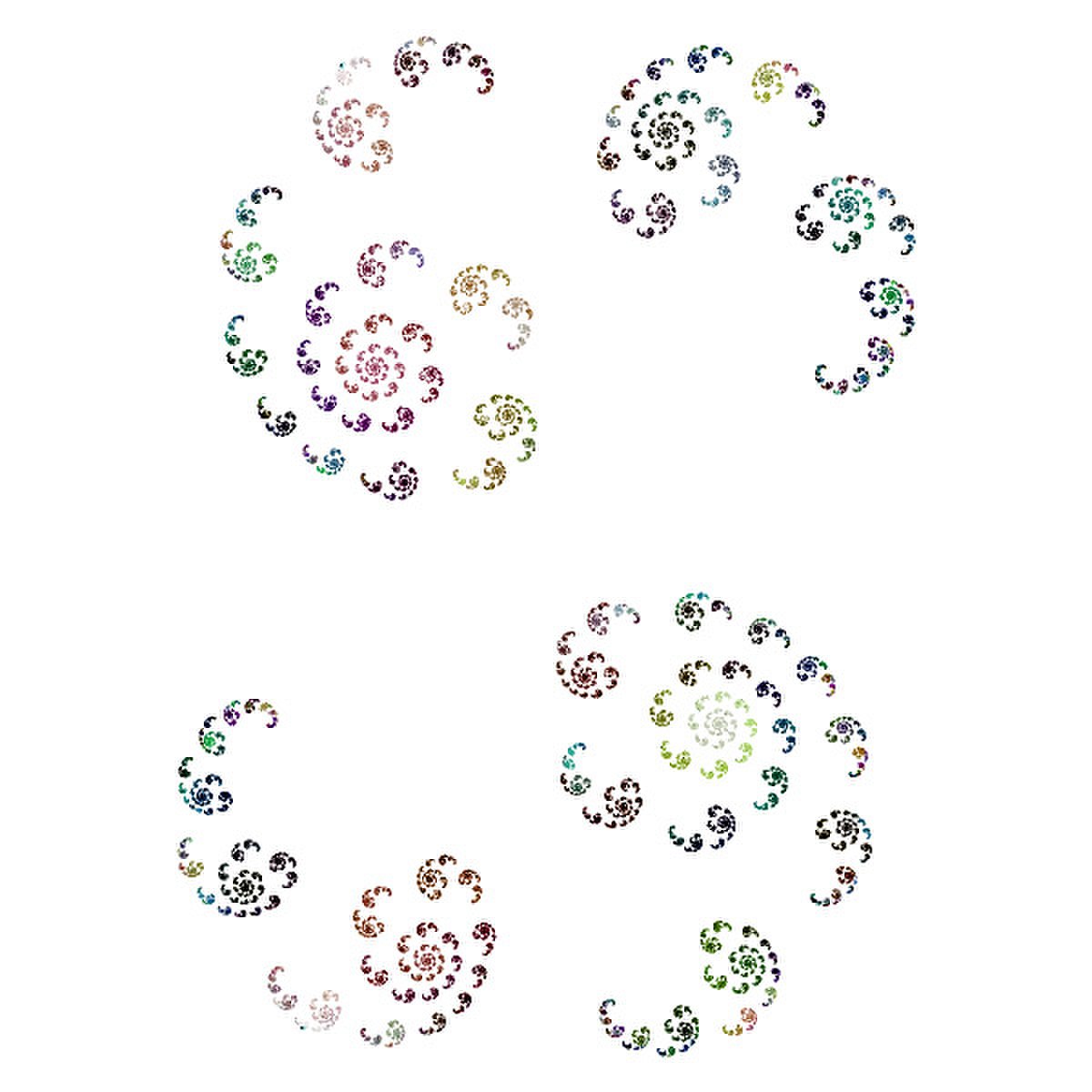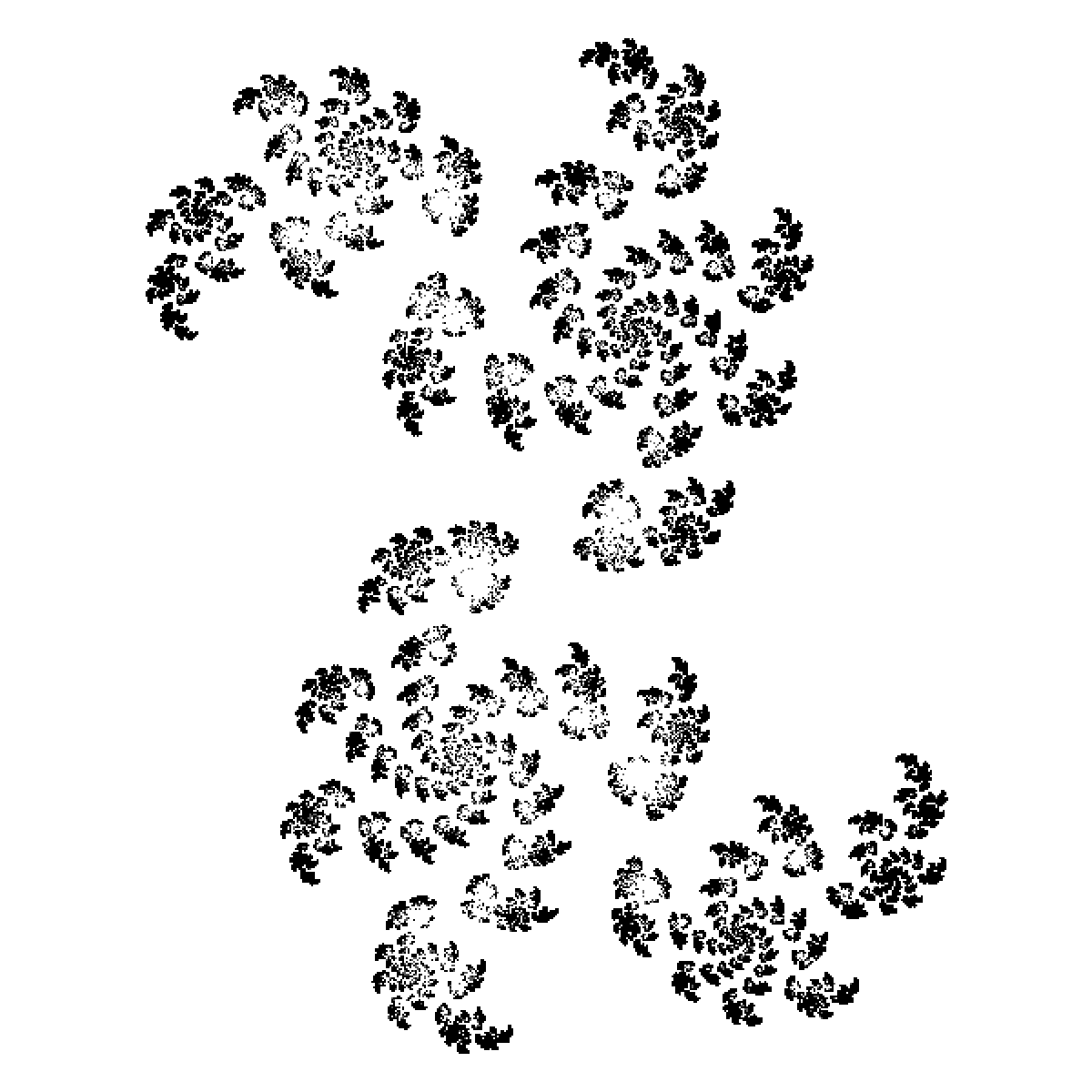Ensemble de Julia - Définition

Introduction

Un ensemble de Julia

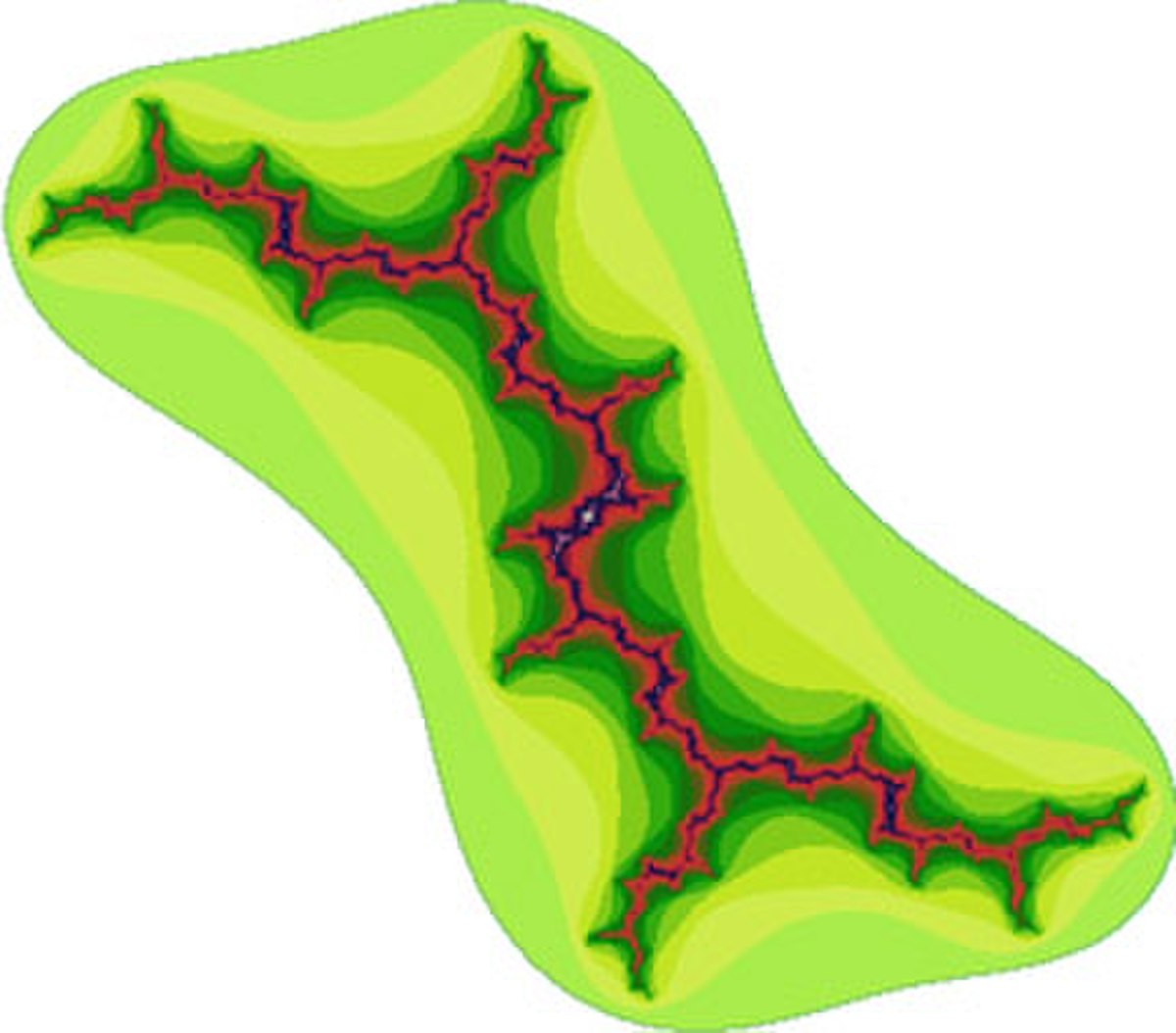
Les ensembles de Julia J(f), décrits par Gaston Julia, sont des fractales, sous-ensembles du plan complexe associés au comportement dynamique d'une fonction holomorphe f. Cet article ne décrit que le cas particulier de la fonction

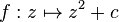
Définition

Étant donnés deux nombres complexes, c et z₀, définissons la suite (z_n) par la relation récurrente :

z_n+1 = z_n² + c

Pour une valeur donnée de c, l'ensemble de Julia correspondant est formé de toutes les valeurs initiales z₀ pour lesquelles la suite est bornée. La définition des ensembles de Julia est relativement proche de celle de l'ensemble de Mandelbrot qui est l'ensemble de toutes les valeurs de c, pour lesquelles la suite des modules ne tend pas vers l'infini, en prenant z₀=0+0i=0.

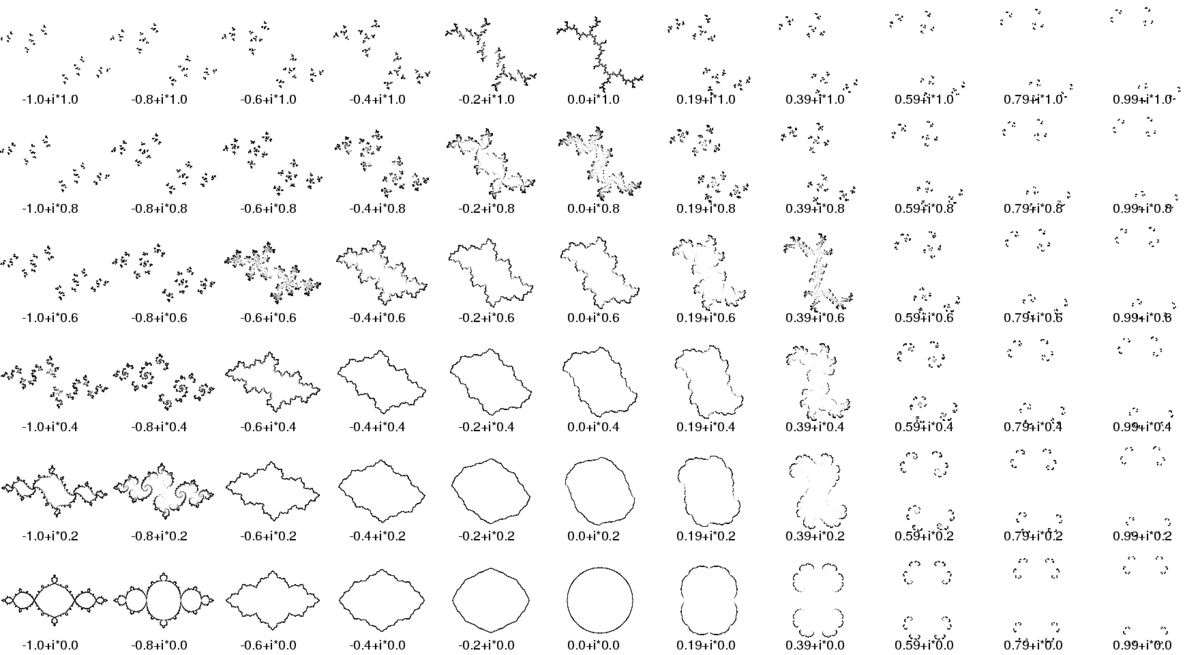
L'ensemble de Mandelbrot est, d'une certaine façon, un ensemble d'indices pour tous les ensembles de Julia. À tout point du plan complexe (qui représente une valeur de c) correspond un ensemble de Julia.

Nous pouvons imaginer un film sur lequel nous voyons défiler les ensembles de Julia correspondant à un point qui se déplace dans le plan complexe.

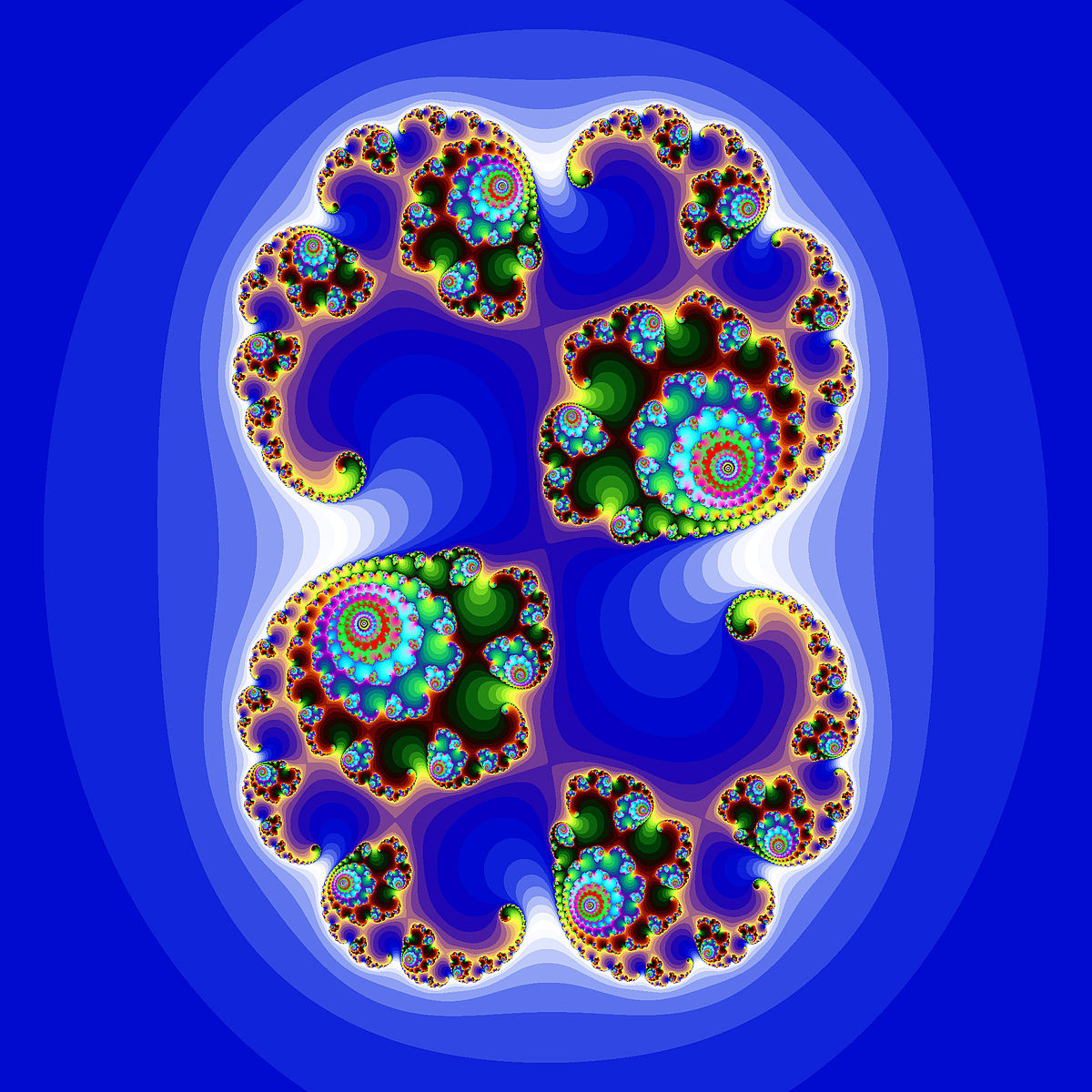
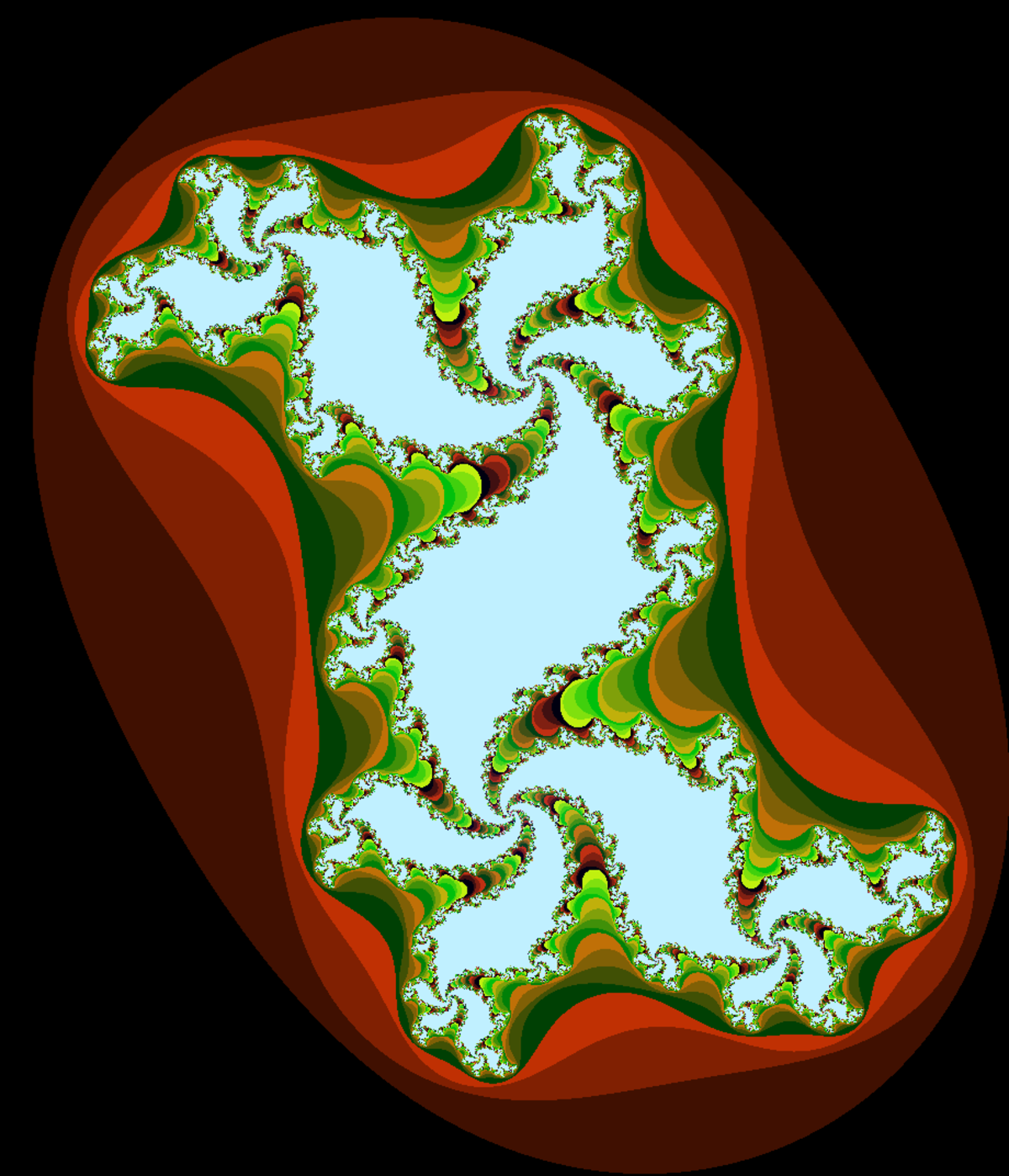
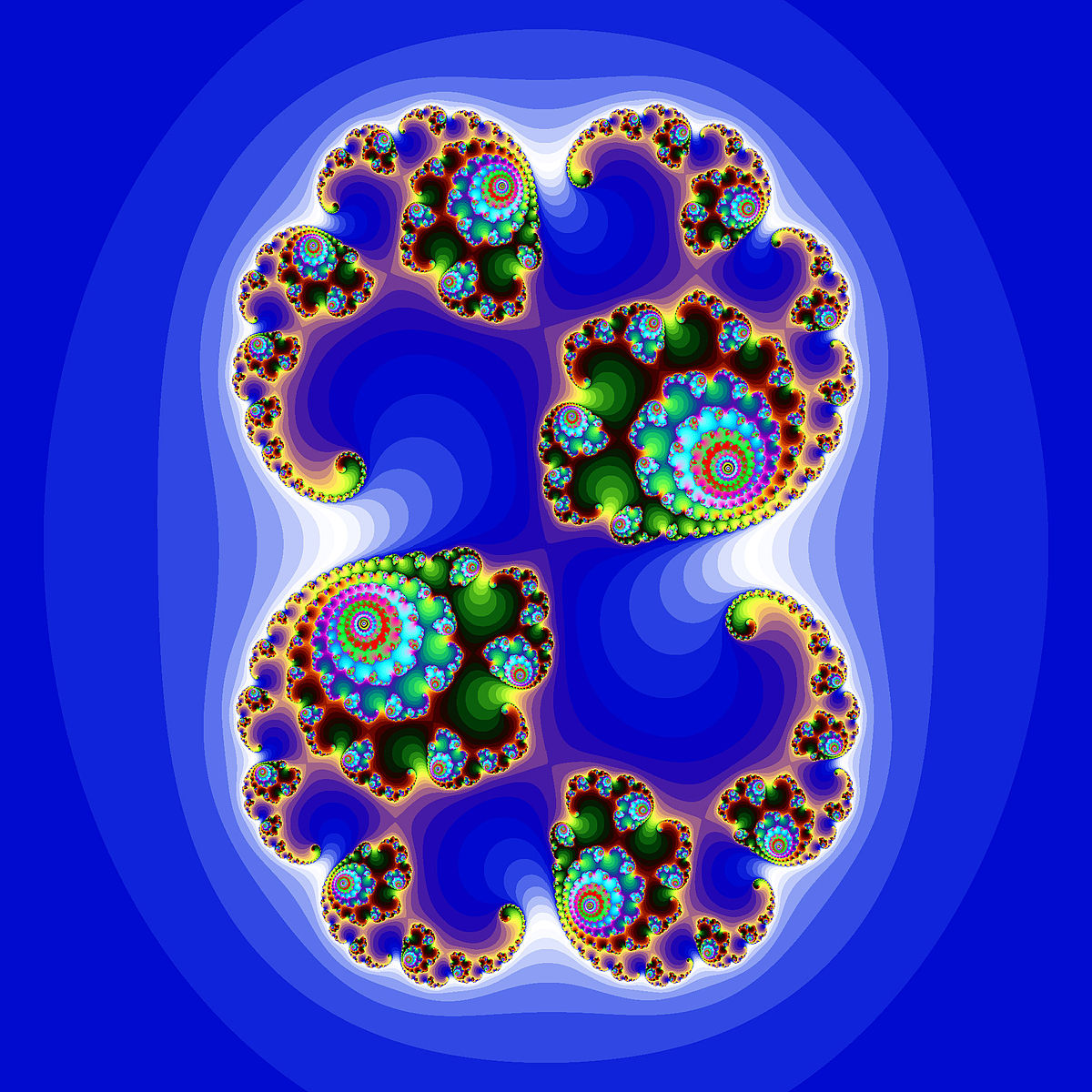
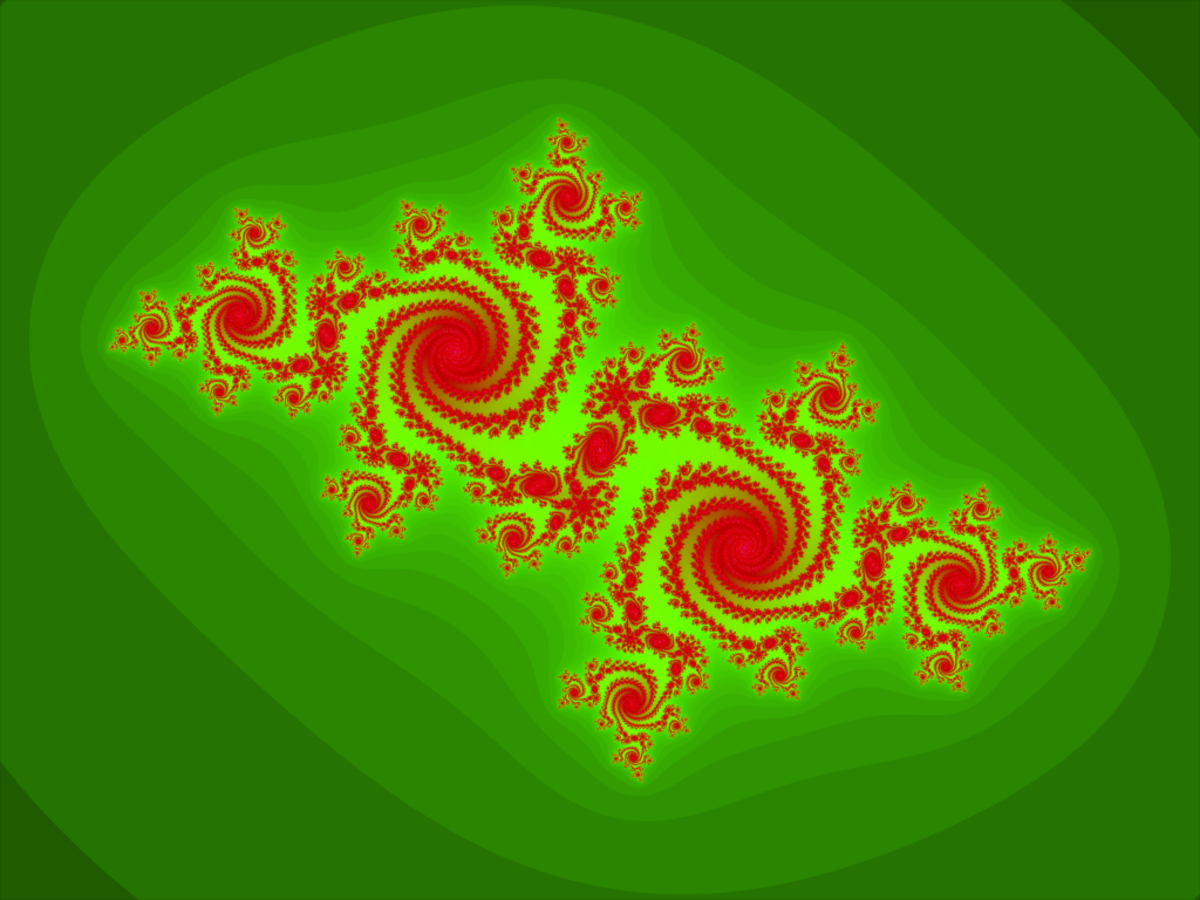
Quand le point appartient à l'ensemble de Mandelbrot, l'ensemble de Julia correspondant est d'« une seule pièce » c'est-à-dire topologiquement connexe.

Lorsque le point traverse la frontière de l'ensemble de Mandelbrot, l'ensemble de Julia se brise en une poussière de Cantor formée de points non connectés.

Images

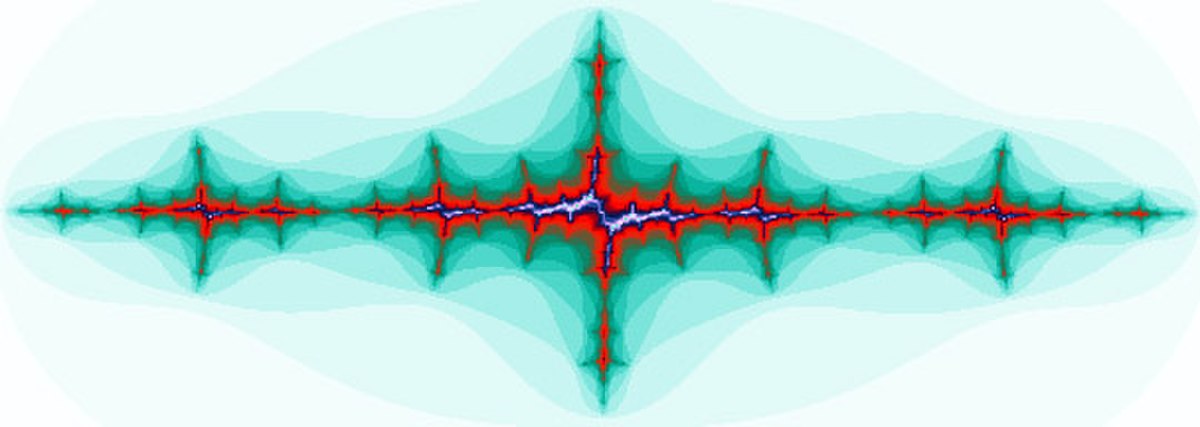
Images 2D

Julia-Menge	escape-time function	Speciale couleur-mapping	Detail
Detail	image en haute résolution	image en haute résolution	Formule inversée.
Formule inversée.	Formule inversée.	Formule inversée.
Formule inversée.		animation zoom
			Time escape Julia avec coordonnées (phi-2, phi-1)
Time escape Julia avec coordonnées (phi-2,0)	Time escape Julia avec coordonnées(0.285, 0)

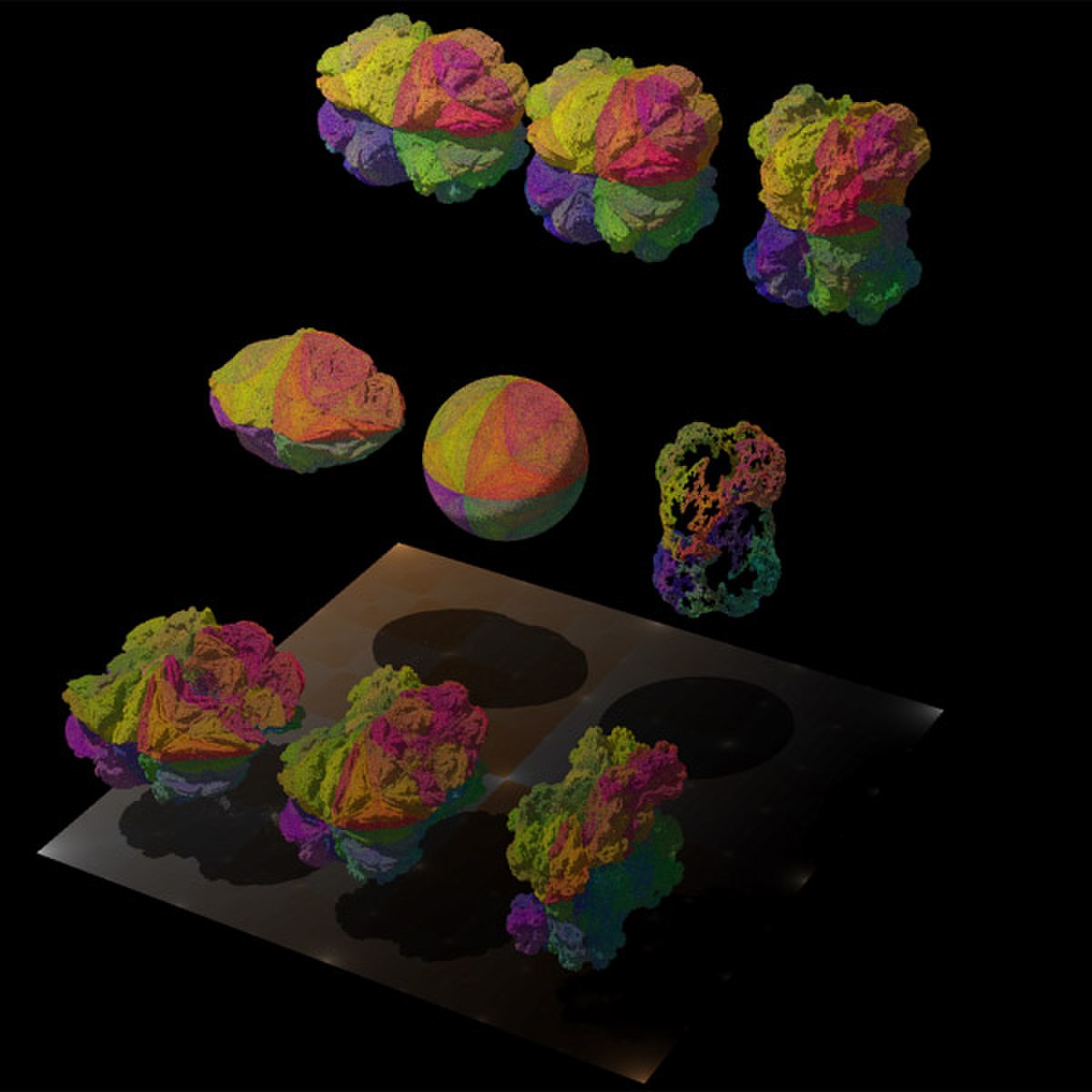
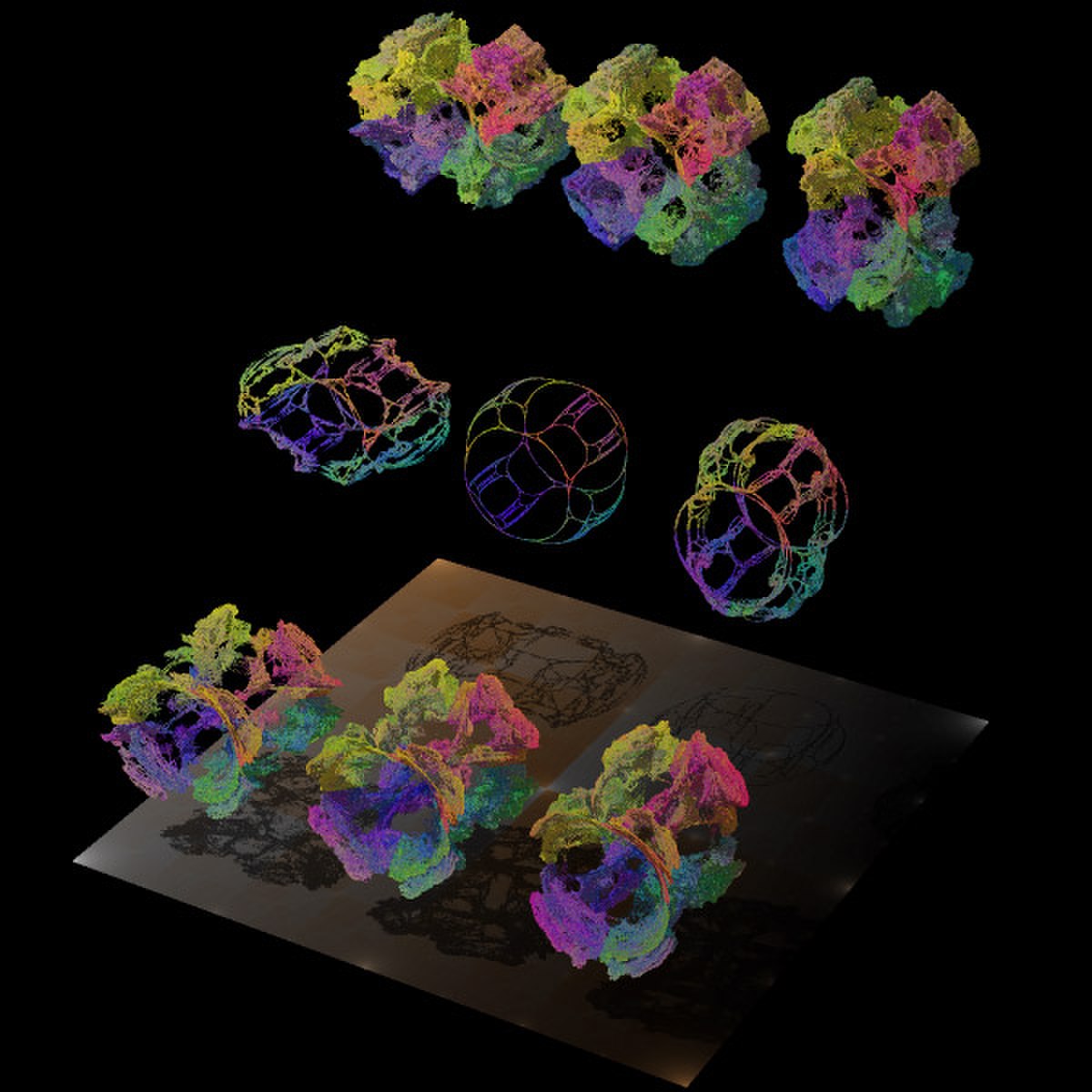
Images 3D

Quaternion , (4D).	3D - 4D Quaternion