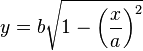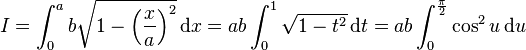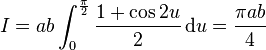Ellipse (mathématiques) - Définition
La liste des auteurs de cet article est disponible ici.
Équations caractéristiques
Équation cartésienne
Dans le repère défini par le grand axe et le petit axe de l'ellipse, son équation est (si l'axe focal est x) :
si l'axe focal est y alors a et b sont inversés
Si une ellipse n'est pas centrée à l'origine d'un système de coordonnées, mais que son grand axe et son petit axe restent parallèles aux axes des coordonnées, celle-ci peut être spécifiée par l'équation suivante :
où les paramètres h et k sont les coordonnées du centre de l'ellipse.
Comme toute conique, une ellipse possède une équation de la forme :
B vaut 0 si les axes de l'ellipse sont parallèles à ceux de coordonnées.
Paramétrisation
dans le repère défini par le grand axe et le petit axe. Avec (h,k) les coordonnées du centre de l'ellipse.
Équation polaire
dans le repère défini par le foyer et l'axe focal.
ou
dans le repère défini par le centre et l'axe focal.
Tracer une ellipse
- Méthode des deux points et de la corde : selon la , la somme AF + AF' des distances entre un point A de l'ellipse et ses deux foyers F et F' est constante. Ainsi, on plante deux piquets dans le sol (les deux foyers), on prend une corde non élastique de longueur donnée (la somme constante) que l'on attache aux piquets; le trajet que l'on parcourt en maintenant la corde tendue est une ellipse. On nomme cette technique celle de « l'ellipse du jardinier ».
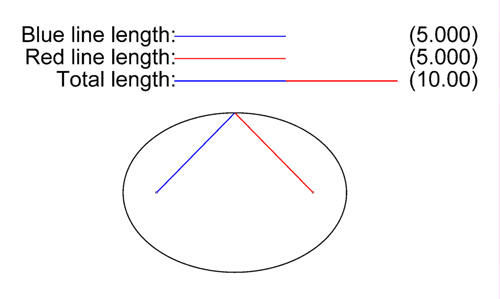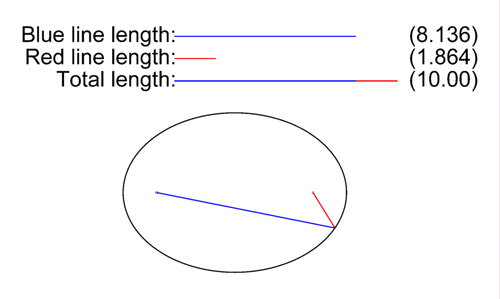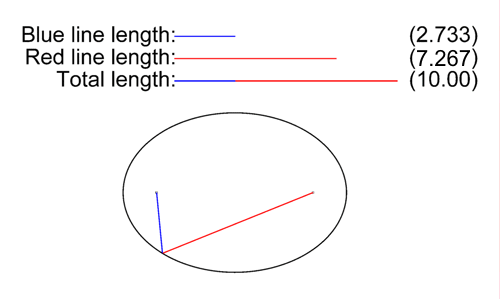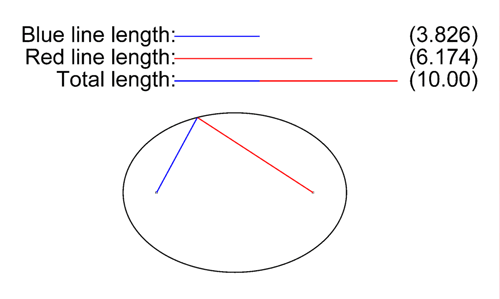 Tracé d'une ellipse à l'aide de deux piquets et d'une corde non élastique tendue
Tracé d'une ellipse à l'aide de deux piquets et d'une corde non élastique tendue - En dessin industriel, une ellipse est en général un cercle vu en perspective (une pièce est rarement elliptique même si ce n'est pas exclu), ou bien un perçage en biais par rapport à la surface de la pièce. L'ellipse se représente donc avec les mêmes traits d'axe que pour le cercle. Dans le cas d'un cercle vu en perspective, ces traits d'axe sont inclinés et suivent les directions de référence. Dans le cas d'une forme réellement elliptique, les traits d'axes sont perpendiculaires.
- Tracé à main levée, méthode du parallélogramme exinscrit : on a vu ci-dessus qu'une ellipse pouvait être considérée comme un cercle vu en perspective. De même qu'un cercle est inscrit dans un carré, une ellipse est inscrite dans un parallélogramme qui n'est autre que ce carré vu en perspective cavalière (notez qu'il existe une infinité de parallélogrammes circonscrits, il suffit d'en choisir un). On trace d'abord un parallélogramme, on le divise en quatre quartiers selon les parallèles aux côtés passant par les milieux des autres côtés ; dans chaque quartier, on trace un arc passant par les milieux des côtés et tangent aux côtés en ces milieux (certaines caractéristiques de sécantes dans le cercle permettent de trouver d'autres points de passage intermédiaires de ces arcs).
Aire du domaine intérieur à une ellipse
Il existe différentes manières de calculer l'aire d'une ellipse. On peut se placer dans le repère porté par les axes où l'équation de l'ellipse s'écrit :
Avec les symétries établies plus haut, il suffit de calculer par exemple l'aire de la portion d'ellipse dans le quart supérieur droit du plan rapporté à ce repère. L'équation de la portion d'ellipse correspondante est :
pour x dans [0,a]. D'où l'aire du quart supérieur droit d'ellipse :
la dernière réécriture obtenue avec le changement de variable
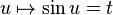
et pour l'aire de toute l'ellipse :
- S = πab
Remarquer que pour a = b, on retrouve l'aire du cercle.
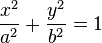
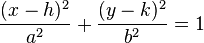
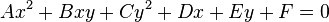
![[2] \qquad \begin{cases}x = h+ a\cos t \\ y =k + b\sin t \end{cases} \quad t \in\R](https://static.techno-science.net/illustration/Definitions/autres/8/8052c1007487e997a965f33170402078_b8164a620e9eb912d9665da6039e02da.png)
![[3a] \qquad r(\theta) = \frac{p}{1+e \cos \theta} \qquad \theta \in\R](https://static.techno-science.net/illustration/Definitions/autres/b/bb929ab4cdb54d81f04b7ff00b84e8bc_b5a4b69774a79d0a0dbcbee7985906fb.png)
![[3b] \qquad r^2(\theta) = \frac{b^2}{1-e^2 \cos ^2 \theta} \qquad \theta \in\R](https://static.techno-science.net/illustration/Definitions/autres/3/30620da3260564cc414b2c56a0dd8a67_780b8cfe1e1fc62d84431d8a7770102b.png)