Écoulement de Poiseuille - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Principe - Champ de vitesse entre deux plaques - Champ de vitesse dans un tube - Démonstration (dans le cas du tube)

Champ de vitesse entre deux plaques

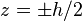
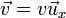
On suppose que le gradient de pression est orienté selon l'axe $x$ et que la normale aux plaques est orientée selon $z$ , avec les plaques situées en $z = \pm h/2$ . La vitesse est alors parallèle aux plaques, et plus précisément orientée selon l'axe $x$ : $\vec{v} = v \vec{u}_x$ .

Équation du profil de vitesse :

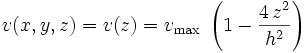
$v(x,y,z) = v(z) = v_{\rm max}\;\left( 1-\frac{4\,z^2}{h^2} \right)$

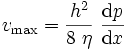
où la vitesse maximale (au milieu de la couche) est liée au gradient de pression, à la viscosité dynamique et à la distance entre les plaques : $v_{\rm max} = \frac{h^2}{8\;\eta} \; \frac{{\rm d} p}{{\rm d} x}$

La démonstration de ce résultat est similaire à celle donnée ci-dessous dans le cas du tube circulaire.

Champ de vitesse dans un tube

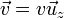
La vitesse est parallèle à l'axe du tube (noté $z$ ) : $\vec{v} = v \vec{u}_z$ .

Équation du profil de vitesse :

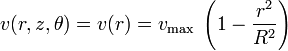
$v(r,z,\theta) = v(r) = v_{\rm max}\;\left( 1-\frac{r^2}{R^2} \right)$

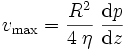
où la vitesse maximale (au centre du tube) est liée au gradient de pression, à la viscosité dynamique et au rayon : $v_{\rm max} = \frac{R^2}{4\;\eta} \; \frac{{\rm d} p}{{\rm d} z}$

La démonstration de ce résultat est donnée plus bas.

Démonstration (dans le cas du tube)

1. Par symétrie, l'écoulement ne varie ni en $z$ , ni en $θ$ :

$v (r, z,θ) = v (r)$

2. Par conséquent, les seuls efforts de cisaillement sont des forces selon $z$ transmises radialement (selon $r$ ) :

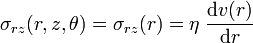
$\sigma_{rz}(r,z,\theta) = \sigma_{rz}(r) = \eta\;\frac{{\rm d} v(r)}{{\rm d} r}$

3. Par symétrie également, la variation de la pression est constante le long de l'axe $z$ :

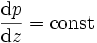
$\frac{{\rm d} p}{{\rm d} z} = {\rm const}$

4. Considérons les efforts subis par une zone cylindrique de rayon $r$ et de longueur $Δ z$ .

Les efforts de pression sur les deux faces circulaires du cylindre ont une résultante égale à :

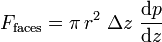
$F_{\rm faces} = \pi\,r^2 \; \Delta z \; \frac{{\rm d} p}{{\rm d} z}$

Les contraintes de cisaillement sur le bord du cylindre lui transmettent une force orientée selon son axe $z$ :

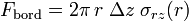
$F_{\rm bord} = 2\pi\,r \; \Delta z \; \sigma_{rz}(r)$

Le gradient de pression se transmet aux parois en tant que contrainte de cisaillement.

La force totale exercée sur le cylindre de liquide est nulle puisque l'écoulement est permanent. Ainsi :

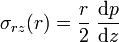
$\sigma_{rz}(r) = \frac{r}{2} \; \frac{{\rm d} p}{{\rm d} z}$

5. Il s'ensuit que le gradient de vitesse est linéaire en $r$ :

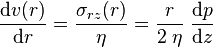
$\frac{{\rm d} v(r)}{{\rm d} r} = \frac{\sigma_{rz}(r)}{\eta} = \frac{r}{2\;\eta} \; \frac{{\rm d} p}{{\rm d} z}$

6. Autrement dit, le champ de vitesse est parabolique :

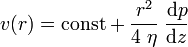
$v(r) = {\rm const} + \frac{r^2}{4\;\eta} \; \frac{{\rm d} p}{{\rm d} z}$

7. Compte tenu de la condition de non-glissement ( $v (R) = 0$ ) :

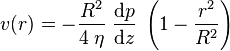
$v(r) = -\frac{R^2}{4\;\eta} \; \frac{{\rm d} p}{{\rm d} z} \; \left( 1-\frac{r^2}{R^2} \right)$

La vitesse est plus importante au centre du conduit malgré le signe négatif, étant donné que la vitesse est orientée à l'encontre du gradient de pression. Écoulement dans le sens positif pour un gradient négatif... CQFD

Principe

- Introduction - Principe - Champ de vitesse entre deux plaques - Champ de vitesse dans un tube - Démonstration (dans le cas du tube)

Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀

Record établi pour un transistor en diamant 💎

Les sursauts radio rapides trahissent enfin leur origine cosmique 📡

Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠

Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊

Les oscillations collectives des foules humaines denses 🔁

Une forme inconnue de la matière détectée au LHC ? ⚛️

Le sel, un facteur méconnu de l'obésité ? 🧂

L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀

Découverte tectonique majeure sous les Petites Antilles 🌍

Peut-on geler en chauffant ? ❄️

Une peau électronique pour doter les robots du sens du toucher 👌

Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳

Le cancer inscrit dans nos gènes dès la naissance ? 🧬

Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥

Le passé verdoyant du plus grand désert du monde 🐪

Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷

Des puces quantiques plus proches que jamais ⚡

Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬

En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊

Des scientifiques parviennent à produire efficacement du carburant à partir de monoxyde de carbone 🛢️

Que nous apprend la découverte de cet insecte de 16 millions d'années ? 🐜

Avec 91km, l'accélérateur FCC fera passer le LHC pour un jouet ⚛️

Cette vitamine développe les fonctions cognitives du cerveau 🧠

Comment des impacts géants vaporisent les corps planétaires ☄️

Les Américains riches vivent moins longtemps que les Européens pauvres 💰

Attention à ce riz naturellement riche en arsenic 🍚

L'intelligence artificielle contre la mort subite 💀

L'inévitable formation d'un océan de magma basal sur Terre 🔥

Découverte d'une plante étrange sans chlorophylle 🌱

Existe-t-il des mélodies naturelles ? 🎶

Cette exoplanète présente une signature de vie bien plus forte que celle de la Terre 👽

L'origine énigmatique des rayons cosmiques les plus énergétiques ⚡

Le diagnostic de l'autisme remis en cause par l'intelligence artificielle 🩺

Imprimer en 3D avec la lumière du soleil ☀️

La pollution atmosphérique nuit gravement au cerveau 🧠

Le trou noir supermassif Ansky vient de se réveiller ⚫

Voici ce qui rend notre cerveau vraiment unique 🧠

Asymétrie matière-antimatière: une nouvelle pièce du puzzle dévoilée 🧩

Neige en inuit, goût en japonais... comment les langues décomposent la réalité ? 💬

La physique révèle les secrets d'un strike parfait au bowling 🎳

Le TDAH associé à la démence 🧠

Découverte d'une nouvelle forme d'intrication quantique, une première en 20 ans ⚛️

Le régime cétogène montre des surprises sur le cholestérol 🧐

Un tango observationnel révèle une Super-Terre 🔭

Cette expérience montre que la graisse brune augmente fortement la longévité 🕒

L'Univers comme jamais vu auparavant: les révélations du fond diffus cosmologique 🔭

C'est sérieux: de la bave pourrait révolutionner la conception de bioplastiques 🪱

Découverte: le trou noir central de notre galaxie pourrait anéantir la vie sur Terre 💥

Etude scientifique: ces aliments nous font vieillir 🍽️

Page générée en 0.094 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise