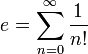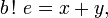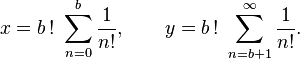E (nombre) - Définition

Démonstration de l'irrationalité de e

Le nombre e est égal à la somme de la série de l'exponentielle de 1 :

Ce développement peut être employé pour montrer qu'il est irrationnel.

Démonstration.

Il s'agit de prouver que pour tout entier , le nombre n'est pas entier.

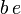
Pour cela, montrons que lui-même n'est pas entier, en le décomposant sous la forme

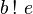
où les nombres x et y sont définis par :

• Le nombre x est entier, car pour tout entier n compris entre 0 et b, n! divise b! : les quantités sont donc entières, donc leur somme x est un entier.
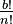
• Le nombre y n'est pas entier, car il est strictement compris entre 0 et 1. En effet,

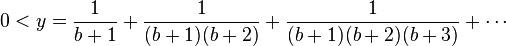
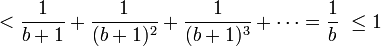
Ici, la dernière somme est une série géométrique de raison .

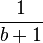
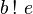
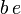
Puisque est somme d'un entier et d'un non-entier, il n'est pas entier ; a fortiori, n'est pas entier, et cela pour n'importe quel entier . Ainsi doit être irrationnel. CQFD

Une autre démonstration consiste à établir le développement en fraction continue du nombre e. Si la preuve est plus complexe, elle offre aussi plus de possibilités de généralisation. Elle permet de montrer que si x est un nombre rationnel non nul, alors e^x est irrationnel. Elle permet aussi d'établir que e n'est pas un irrationnel quadratique, c'est-à-dire n'est solution d'aucune équation du second degré à coefficients rationnels (cf. Fraction continue et approximation diophantienne). En revanche, pour aller plus loin, c'est-à-dire que pour montrer que e n'est solution d'aucune équation du troisième degré à coefficients rationnels, puis qu'il est transcendant, ce qui signifie qu'il n'est solution d'aucune équation polynomiale à coefficients rationnels, de nouvelles idées sont nécessaires.

Définitions et propriétés

Définitions de e

Les considérations précédentes montrent que e peut être défini de plusieurs façons différentes

• e est le réel tel que ln(e) = 1 lorsqu'on définit la fonction ln comme la primitive de la fonction qui s'annule en 1. C'est pourquoi cette constante est aussi appelée la base des logarithmes naturels
• e est le réel tel que exp(1) = e lorsqu'on définit la fonction exp comme l'unique fonction vérifiant u' = u et u(0) = 1.
• e est la limite de la suite .
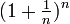
• e est égal à la somme de la série infinie (avec la convention 0! = 1).

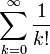
L'équivalence de ces quatre définitions provient des relations qui lient la fonction exponentielle, la fonction logarithme et les limites de suites.

Théorie des nombres

Leonhard Euler

La constante de Néper apparaît largement dans la théorie des nombres. Les mathématiciens se sont très tôt intéressés à la nature du nombre e. L'irrationalité de e fut démontrée par Euler en 1737 et l'irrationalité de ses puissances entières par Lambert en 1761. La démonstration peut se faire grâce à son développement en série (voir la , ci-dessous) soit par son développement en fraction continue.

La preuve de la transcendance de e fut établie par Hermite en 1873. On en déduit que, pour tout rationnel r non nul (ce qui inclut les entiers naturels), e^r est aussi transcendant ; le théorème de Gelfond-Schneider permet de démontrer également que, par exemple, e^π est transcendant, mais on ne sait pas encore (2009) si e^e et π^e sont transcendants ou non.

Les propriétés de ce nombre sont à la base du théorème d'Hermite-Lindemann.

Il a été conjecturé que e était un nombre normal.

Fonction exponentielle et équation différentielle

Pour tout réel x, exp(x) = e^x où exp est l'unique fonction y vérifiant l'équation différentielle y' = y et y(0) = 1. Cette fonction est appelée fonction exponentielle de base e.

Elle permet de donner toutes les solutions de l'équation différentielle y' = ay qui sont les fonctions définies par f(x) = Ce^ax.

La fonction exponentielle admet le développement en série suivant :

Fonction trigonométrique

La recherche de l'unique solution complexe à l'équation différentielle u' = iu et u(0) = 1 conduit à la fonction u(x) = e^ix = cos(x) + isin(x) et à l'identité d'Euler :

e^iπ + 1 = 0

qui selon Richard Feynman est « la formule la plus remarquable du monde » (e représentant l'analyse, i l'algèbre, π la géométrie, 1 l'arithmétique et le nombre 0 les mathématiques). Euler lui-même aurait également été émerveillé de cette relation rassemblant cinq nombres fondamentaux : 0, 1, e, i, π.