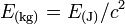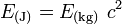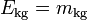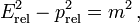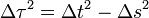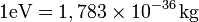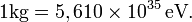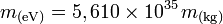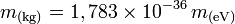E=mc2 - Définition

Unités

Énergie en unités de masse

Les formules utilisées ci-dessus sont écrites en unités conventionnelles. Mais il peut être commode d'utiliser des unités mieux adaptées à l'espace-temps, en exprimant en particulier une énergie en kilogrammes, autrement dit en prenant comme unité d'énergie l'énergie d'un kilogramme de matière.

D'après la formule :

E(joules) = m(kilogrammes)×[c(m/s)]²,

l'énergie équivalente à la masse d'un kilogramme est :

énergie d'un kilogramme (en joules) = [c(m/s)]².

Par conséquent l'énergie en unités de masse sera :

E(en unités de masse) ≡ E(en kilogrammes) = E(en joules)/(énergie d'un kilogramme en joules) ≡ E(en joules)/[c(m/s)]²

On peut donc écrire :

et en sens inverse :

Numériquement :

1 kg = 8,988×10¹⁶ J

1 J = 1,113×10^-17 kg

ou dans le système CGS utilisé par habitude en astronomie :

1 g = 8,988×10²⁰ erg

1 erg = 1,113×10^-21 g

De la même façon, la réunion du temps et de l'espace en une seule entité invite le physicien à utiliser une même unité, la seconde ou le mètre, pour mesurer les longueurs et les temps.

On a les formules de passage suivantes :

,

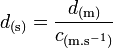
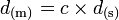
où d est le temps mis par la lumière pour parcourir d.

On écrit à l'identique :

,

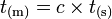
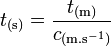
où t est la distance parcourue par la lumière en t.

L'utilisation d'une unité commune, disons la seconde, pour mesurer distance et temps est riche d'enseignement dans le contexte présent. En effet grâce à ce choix la vitesse v, rapport d'une distance à un temps, devient sans dimension. Par conséquent l'énergie cinétique newtonienne K = (1/2)mv² prend les dimensions d'une masse, ce qui revient à dire qu'on peut exprimer une énergie en unités de masse. On retrouve donc de façon simple, et néanmoins convenable, l'équivalence entre énergie et masse.

Ainsi, si l'énergie E est exprimée en unités de masse (par exemple en kilogrammes) la formule d'Einstein devient :

ou plus simplement :

.

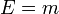
En fait, en utilisant des unités relativistes, le facteur c disparaît de toutes les formules. Ainsi la formule donnant l'invariant du vecteur énergie-impulsion s'écrit maintenant :

où E et p sont exprimées en unités relativistes (c'est-à-dire en kilogrammes).

De même il est agréable d'écrire le carré du temps propre sous la forme homogène et symétrique :

sans avoir à traîner des facteurs c.

Masse en électron-volt

En sens inverse il est très courant en physique atomique de mesurer une masse en unités d'énergie. Ainsi la masse d'une particule est souvent donnée en électron-volt.

Un électron-volt vaut 1,602 176 53×10^-19 joule, énergie à laquelle correspond la masse 1eV/c², soit 1,783×10^-36 kg.

On a donc les formules de passage :

Puisque le nombre sans dimensions qui mesure une certaine grandeur est par définition le rapport entre la grandeur à mesurer et la grandeur choisie pour unité, ce nombre est inversement proportionnel à la valeur de l'unité choisie (si l'unité choisie est plus grande, le nombre qui mesurera la grandeur est lui plus petit).

Ici on a donc :

m(en eV) / m(en kg) = 1kg / 1eV,

de sorte que l'on peut écrire :

Rappelons les multiples usuels :

1 keV = 10³ eV

1 MeV = 10⁶ eV

1 GeV = 10⁹ eV

1 TeV = 10¹² eV

Par exemple, la masse de l'électron est de 511 keV, celle du proton de 938 MeV et celle du neutron est de 940 MeV.