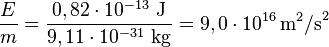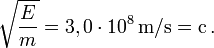E=mc2 - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Historique - Formulation générale - Illustrations - Unités - Cas d'une particule de masse nulle - Autre notation - Énergie d'une particule

Illustrations

En mécanique newtonienne, l'énergie d'une particule isolée provient de sa vitesse et se manifeste sous forme d'énergie cinétique. Au contraire, d'une façon inattendue à l'époque de sa découverte, E = mc² exprime qu'une particule de masse m possède intrinsèquement une énergie E, même si elle est au repos. Elle stipule que la masse est une forme d’énergie comme le sont l’énergie potentielle ou l’énergie cinétique. L’énergie d’un corps devient donc la somme de son énergie cinétique et de sa masse.

Cette équivalence entre masse et énergie ouvre un éventail de possibilités inconnues de la physique pré-relativiste. En relativité restreinte, la masse peut être convertie en chaleur, énergie cinétique ou autre forme d’énergie. En effet lorsque les particules d'un système donné subissent une transformation, par exemple lors d'une collision, la relativité restreinte impose que l'énergie totale (évaluée dans un certain système de coordonnées) se conserve. Mais comme l'énergie comprend la masse, il est tout-à-fait possible que de la masse apparaisse lors de la réaction (par exemple sous forme de particules) au détriment d'énergie ou que, au contraire, de l'énergie soit libérée par « consommation » de masse.

Numériquement, dans l'équation $E = m c 2$ et dans le système international d'unités :

E est l'énergie exprimée en joules,
m est la masse en kilogrammes,
c est la vitesse de la lumière dans le vide, soit 299 792 458 m/s = 2,997 924 58×10⁸ m/s (soit c ≈ 300000 km/s), ce qui correspond à un facteur c² ≈ 9×10¹⁶ m²⋅s^-2.

Dans le système CGS, E est en erg, m en grammes, c vaut 2,997 925×10¹⁰ cm/s et c² ≈ 9×10²⁰ cm²⋅s^-2.

Ce type de transformation de masse en énergie est utilisée par les piles atomiques ainsi que des bombes nucléaires. L’énergie correspondant à 1 kg de matière est énorme, car égale à 9×10¹⁶ joules : c'est l’énergie produite par un réacteur nucléaire d'une puissance de 1400 MW pendant deux ans environ. La France a produit en 2006 environ 80 % de son électricité dans des centrales nucléaires dont le bilan d'énergie peut être évalué à partir de la formule d'Einstein.

Domaine d'application général de la formule

Mais cette relation n'est pas réservée au domaine du nucléaire. Par exemple en chimie, lorsque 1 kg d'hydrogène se combine avec 8 kg d'oxygène pour former de l'eau, environ 10⁸ joules d'énergie est libérée. Cette énergie correspond à une perte de masse d'environ 10^-9 kg, ce qui entraine que la masse de l'eau formée est inférieure de cette quantité à la masse initiale de 9 kilogrammes des réactifs.

Cependant le défaut de masse, de l'ordre du dixième de milliardième en valeur relative, est trop infime pour pouvoir être mis en évidence par des mesures expérimentales, qui arrivent au mieux à l'ordre du centième de millionième. C'est pour ça que l'on continue à utiliser le « théorème classique » de la conservation de la masse dans les réactions chimiques et dans la vie courante, mais en toute rigueur c'est inexact.

Néanmoins, les mesures de spectrométrie de masse les plus pointues approchent cet ordre de précision. Et alors on pourra visualiser directement l'équivalent de masse de l'énergie de liaison moléculaire, comme on le fait avec l'énergie de liaison nucléaire.

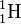
Un autre exemple illustrant l'équivalence entre masse et énergie est donné par le défaut de masse de l'atome le plus simple : la masse de l'atome d'hydrogène $_1^1\mbox{H}$ est inférieure à la somme des masses de l'électron et du proton d'une quantité juste égale à l'équivalent en masse de l'énergie d'ionisation de l'atome, bien que ce défaut soit tout à fait hors de portée de la mesure courante, puisqu'il vaut : $\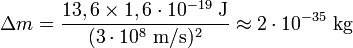Delta m = \frac {13,6\times1,6\cdot10^{-19} \mbox{ J}} {(3\cdot10^8\mbox{ m/s})^2} \approx 2\cdot10^{-35}\text{ kg}$ ; c'est-à-dire un peu plus de dix milliardième (un centième de millionième) de la masse d'un proton...

On peut encore vérifier expérimentalement que la racine carrée du rapport E/m est égale à c dans l'exemple suivant. Dans la désintégration du positronium, il y a création et émission de deux rayons gamma d'énergie (mesurée) 0,511 MeV = 0,8186×10^-13 J, en compensation de la disparition de deux masses d'électron.

La masse d'un électron étant de 9,11×10^-31 kg, on trouve bien :

et donc :

À l'échelle astronomique, la formule explique également comment les étoiles, comme le Soleil, peuvent émettre leur énergie pendant des milliards d'années, alors que cette situation constituait un mystère pour la physique du début du XX^e siècle, aucune source d'énergie connue à l'époque ne pouvant en rendre compte.

Au centre du Soleil, les conditions physiques sont telles que s'y produisent des réactions nucléaires capables au bout d'une chaine de processus de transformer 4 noyaux d'hydrogène (4 protons), en un noyau d'hélium. Il se trouve que la masse au repos du noyau d'hélium (⁴He) est inférieure à la somme des masses au repos des 2 protons et 2 neutrons qui le constituent. L'énergie équivalente à cette différence de masse est la source de l'énergie du Soleil, et grâce à l'importance du facteur de conversion c² et à la masse considérable du Soleil, le calcul montre que l'énergie libérée permet à notre étoile de briller pendant une bonne douzaine de milliards d'années.