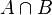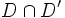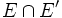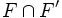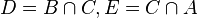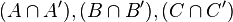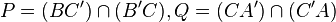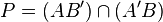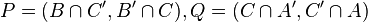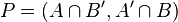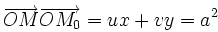Dualité (géométrie projective) - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La dualité projective, crée par Jean-Victor Poncelet (1788 - 1867), père fondateur de la géométrie projective, bien que beaucoup moins enseignée que la dualité en algèbre linéaire, est probablement la plus belle notion de dualité que l'on rencontre en mathématiques.
Il s'agit de formaliser la constatation toute simple qu'il y a une analogie - une dualité, justement - entre le fait que par deux points distincts passe une droite et une seule, et le fait que deux droites distinctes se coupent en un point et un seul (à condition de se placer justement en géométrie projective, de sorte que deux droites parallèles se rencontrent en un point à l'infini).
Dualité dans un plan projectif
Définition
Contrairement à la géométrie plane classique où les droites sont des ensembles de points, il vaut mieux considérer en géométrie projective que le plan projectif P est constitué d'un ensemble de points
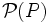
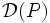
Nous considérons dans un premier temps que le plan projectif P est défini de manière axiomatique ; on constate alors que l'on obtient un autre plan projectif en considérant l'objet P * dont les "points" sont les droites de P et les "droites" sont les points de P, une droite de P * (qui est un point M de P) passant par un "point" de P * (qui est une droite D de P) lorsque D passe par M.
| Voici un point et une droite de P : normal ! | Voici un "point" et une "droite" de P * dont nous avons dessiné 4 de ses "points". |
 |
Pour simplifier, au lieu de travailler sur 2 plans différents, P et P * , on peut se contenter de travailler sur un seul plan projectif P.
- Corrélation ou dualité, déf : Une corrélation est une transformation des points du plan en droites et des droites du plan en points et qui respecte l'incidence.
- Polarité, déf : Une polarité est une corrélation involutive, c’est-à-dire que son carré est la transformation identique.
Exemples
A toute configuration de points et de droites dans P correspond alors dans P * une configuration duale obtenue en échangeant les points et les droites, et de même, à tout théorème dans P, correspond un théorème dual. Voici quelques exemples :
| Configuration dans P | Même configuration vue dans P * |
| 2 points A et B et la droite passant par ces deux points, notée (AB) | 2 droites A et B et leur point d'intersection, noté
|
| 3 points alignés | 3 droites concourantes |
Configuration de Ceva 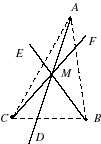 Un triangle de sommets A,B,C et trois céviennes D,E,F concourant en M | Configuration de Ménélaus 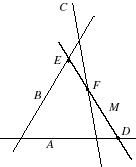 Un triangle de côtés A,B,C et une ménélienne M rencontrant les côtés en D,E,F |
| Configuration de Desargues Deux triangles de sommets respectifs A,B,C et A',B'C', et de côtés D,E,F et D',E',F' (D = (BC),E = (CA) etc), P,Q,R les points
Le théorème de Desargues affirme que P,Q,R sont alignés ssi U,V,W sont concourantes. | Configuration de Desargues (qui est donc "auto-duale") Deux triangles de côtés respectifs A,B,C et A',B'C', et de sommets D,E,F et D',E',F' (
Le théorème de Desargues affirme que P,Q,R sont concourantes ssi U,V,W sont alignés. |
| Configuration de Pappus Deux triplets de points alignés A,B,C et A',B',C',
| Configuration de "Copappus", ou Pappus-dual Deux triplets de droites concourantes A,B,C et A',B',C',
|
Remarque : Si l'on convient d'identifier une droite avec l'ensemble de ses points, il faut, pour que la dualité soit parfaite, identifier un point avec l'ensemble des droites qui passent par ce point, autrement dit, identifier un faisceau de droites avec son pôle !
Dualité et birapport
Dualités, corrélations et polarités
Considérons les homographies de P sur P * ; ce sont des bijections f de
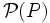
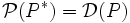

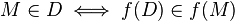
De telles applications sont appelées des dualités ou corrélations ; lorsqu'elles sont involutives (f = f − 1), elles sont appelées des polarités ou autrefois "transformations par polaires réciproques". Dans ce dernier cas, l'image d'un point est appelé la polaire de ce point, et l'image d'une droite, son pôle.
D'après le théorème fondamental de la géométrie projective, dans le cas réel toute dualité provient d'une homographie (dans le cas général, d'une semi-homographie).
Théorème d'incidence et de réciprocité
Il y a deux théorèmes importants qui découlent des définitions.
Théorème d'incidence: Si le point A est incident à la droite d, alors le point dual de d est incident à la droite duale de A.
Théorème de réciprocité polaire: Si le point A est sur la polaire du point B, alors B est sur la polaire de A. Ce théorème est plus puissant que le précédent.
Relations avec la dualité en algèbre linéaire
On sait qu'il existe une bijection entre les points de P et les droites vectorielles d'un espace vectoriel E de dimension 3, et une bijection entre les droites de P et les plans vectoriels de E (un point appartenant à une droite si la droite vectorielle est incluse dans le plan vectoriel).
L'orthogonalité entre E et son dual E * , ensemble des formes linéaires sur E, qui à tout sous-espace vectoriel de E associe un sous-espace vectoriel de E * induit une bijection entre les plans vectoriels de E et les droites vectorielles de E * , et entre les droites vectorielles de E et les plans vectoriels de E * , qui inverse les inclusions.
Il existe donc une bijection canonique entre les points et droites de P * et les droites et plans vectoriels de E * qui respecte les incidences : si un plan projectif P est associé à un espace vectoriel E, le plan dual P * est bien associé à l'espace vectoriel dual E * .
Duale d'une homographie
Une homographie f du plan projectif dans lui-même est une bijection dans l'ensemble des points de P, qui induit une bijection f * dans l'ensemble des droites de P, qui est l'ensemble des "points" de P * : f * est l'homographie duale de f (remarquons que f * (D) = f(D) !) ; on vérifie que si f provient d'un automorphisme
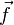
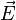
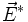
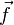
Utilisation des coordonnées
Rapportons le plan projectif P à un repère projectif
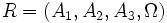
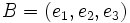

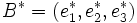

cette équation est l'équation homogène de la droite D image de M par la dualité ; l'on vérifie qu'inversement, l'image de D est M, ce qui fait que cette dualité est une polarité, définie par :
le repère dual
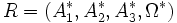
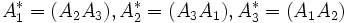
Dualité associée à une forme bilinéaire, polarité associée à une forme quadratique ou à une conique
Soit f une dualité de P vers P * provenant d'un isomorphisme
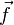
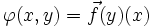
 ) et cette correspondance est bijective ; la dualité f est dite associée à la forme bilinéaire
) et cette correspondance est bijective ; la dualité f est dite associée à la forme bilinéaire

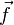

La dualité f est une polarité ssi pour tous points M et N :
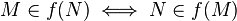

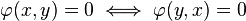

Toute forme quadratique sur E engendre une forme bilinéaire symétrique, laquelle en engendre une polarité dans P, qui est dite associée à q. Le cône isotrope de q (défini par
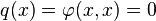
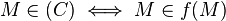
Polarité par rapport à un cercle dans le plan euclidien
Considérons un cercle (C) de centre O de rayon a d'un plan euclidien
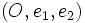
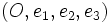
L'équation cartésienne du cercle est x2 + y2 = a2 ; la polarité f par rapport à (C) est donc associée à la forme quadratique X2 + Y2 − a2Z2 de E et l'isomorphisme de E sur E * est celui qui envoie
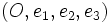
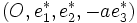
Du point de vue du plan affine
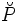
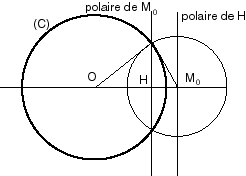 | Et on a les définitions géométriques suivantes : la polaire (droite image par la polarité) d’un point M0(u,v) par rapport au cercle (C) est le lieu des conjugués harmoniques du point par rapport au cercle, lieu défini par la relation
|
Dualité entre courbes
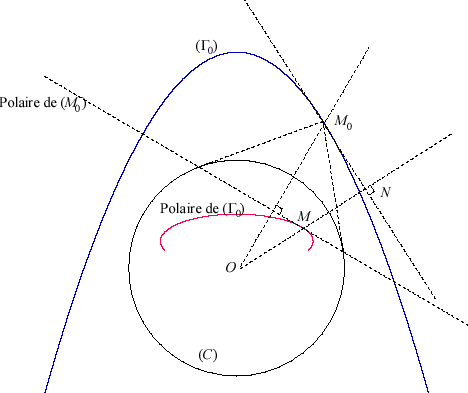 | Une dualité, qui transforme des points en droites et réciproquement, transforme une courbe (Γ0) ( famille de points) de P en une "courbe" (famille de droites) du plan dual P *: mais grâce à la notion d'enveloppe, on retrouve une courbe (famille de points) de P : l'enveloppe de la famille des droites duales, dite courbe duale de (Γ0). Ce qui est remarquable, c'est que lorsque la dualité est une polarité, la duale de la duale est la courbe de départ (autrement dit, la famille des droites polaires des points de la courbe duale enveloppe la courbe de départ). Ci-contre, une figure illustrant ceci, avec une polarité par rapport à un cercle (C). Cette transformation est une transformation de contact : si une famille de courbes admet une enveloppe, la famille des courbes polaires admet pour enveloppe la polaire de cette enveloppe. Voir ici pour plus de détails. |
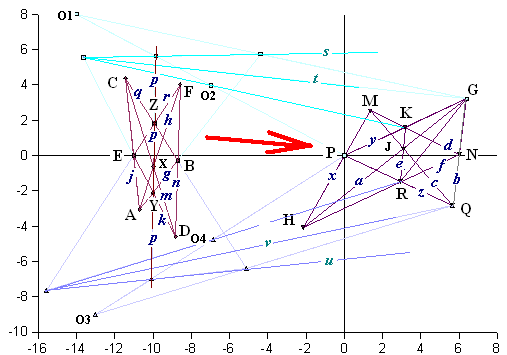
Configuration de Pappus, exemple détaillé de dualité
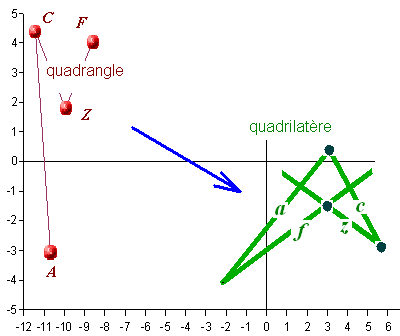
Pour illustrer géométriquement une dualité quelconque, il faut définir le processus par lequel on transforme un point en droite. Un exemple de dualité simple est donné ci-dessous: on prend le quadrangle (4 points) ACZF, on le transforme en quadrilatère (4 droites) aczf, et pour compléter un peu la figure les droites AC, CZ, ZF de la figure de départ ont été tracées, ainsi que les points d'intersection a*c, c*z et z*f de la figure d'arrivée.
-
- Poursuivant le dessin du même exemple, on peut figurer la dualité d'une configuration de Pappus, voir Théorème de Pappus. La configuration de départ est formée des 9 points: AEC DBF XYZ, la configuration d'arrivée est donnée par les 9 droites aec dbf xyz. Dans la configuration de départ on a pris soin de compléter la figure par les 9 droites joignant les points, il s'agit des droites jnp qhk et mgr; de même dans la configuration d'arrivée les intersection des droites donnent naissance aux 9 points JNP QHK MGR.
Cette dualité utilise les points Y,Z, O1, O2, O3 et O4 et les droites y, z, s, t, u et v. La philosophie de la construction est simple.
- Dans la figure de départ un POINT est repéré sur une grille oblique obtenue en croisant deux "éventails" de centres Y et Z. Dans la figure d'arrivée, une DROITE est obtenue en s'appuyant sur deux "échelles" y et z.
-
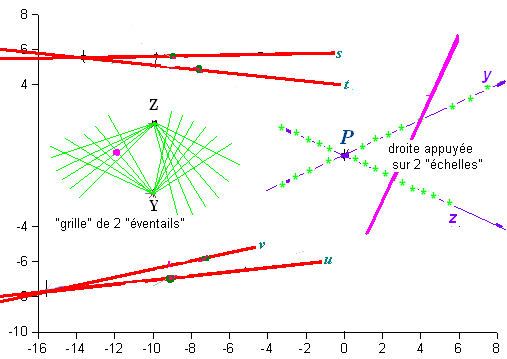
- Le détail de la correspondance entre les "éventails" et les "échelles" est un peu laborieux mais ce n'est qu'un exemple pour montrer qu'une dualité peut être définie de manière complètement géométrique, sans utiliser aucune géométrie analytique, aucune coordonnée homogène.
-
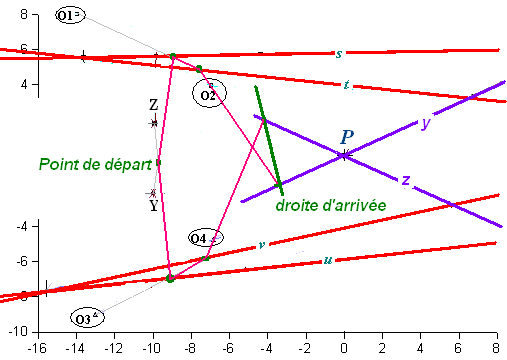
- Le point de départ subit une première triple aventure, il est projeté depuis le centre Y sur la droite s, puis depuis le centre O1 sur la droite t, puis depuis le centre O2 sur la droite y; le premier point de l'"échelle" d'arrivée est obtenu.
- Le point de départ subit une seconde triple aventure, il est projeté depuis le centre Z sur la droite u, puis depuis le centre O3 sur la droite v, puis depuis le centre O4 sur la droite z; le second point de l'"échelle" d'arrivée est obtenu.
- La droite d'arrivée est la droite qui joint ces deux points situés sur les "échelles".
- Une telle opération a été effectuée pour tous les points de la configuration pappusienne (AEC DBF XYZ), ce qui donne les résultats que l'on a dessinés ensuite à l'aide d'un tableur du commerce.
Pour plus de détails, voir aussi Dualité (géométrie projective)/Exemples concrets de constructions duales et polaires