Division - Définition

Algorithme de la division

Cet algorithme sert à déterminer une écriture décimale du quotient de deux nombres entiers, qui se généralise au quotient de deux nombres décimaux

Dans certains cas, la division "ne se termine pas", ce qui signifie que l'algorithme itère à l'infini.

Dans ce cas, le quotient est un rationnel non décimal, et on peut prouver que son développement décimal admet une période, dont la longueur est strictement inférieure au diviseur.

Dans une division non exacte ab (a et b étant deux nombres entiers, b non nul), si on note q_p et r_p respectivement le quotient et le reste obtenus après p en poussant les itérations jusqu'à obtenir p chiffres après la virgule du quotient, on obtient un encadrement ou une égalité :

à 10 ^{− p} près ou

Un nombre irrationnel (réel, sans être rationnel) ne peut s'écrire sous forme de fraction, par définition.

Propriétés

La division n'était pas à proprement parler une opération (loi de composition interne, définie partout), ses "propriétés" n'ont pas d'implications structurelles sur les ensembles de nombres, et doivent être comprises comme des propriétés des nombres en écriture fractionnaire.

"Non-propriétés"

• non-commutative car
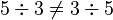
• non-associative car

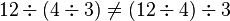
Remarques

• pseudo-élément neutre à droite : 1

  

• pseudo-élément absorbant à gauche : 0

  

• égalité de fractions
  • de même dénominateur

    

  • en général (qui découle de la construction de )

    

• ordre

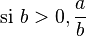  et 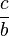sont dans le même ordre que a et c

Mathématiques et langue française

On peut diviser une entité en un nombre de parties dont l'addition donne cette entité, par un moyen implicite ou explicite.

Ainsi, on peut :

• diviser un gâteau en deux parts, par un coup de couteau
• simplement diviser un gâteau en deux [parts, par un moyen quelconque]
• diviser 1 en 2 demis, par la représentation mentale mathématique que l'on s'en fait
• simplement diviser 1 en 36ème
• etc.

On peut également diviser par dichotomie ou par malice, mais diviser par 2 est un concept mathématique.
 : « a divisé par b est égal à c ».