Division euclidienne - Définition

Algorithmes de calcul

On s'intéresse au calcul de division euclidienne de deux entiers, connaissant au préalable les opérations d'addition, de soustraction, de multiplication, et de comparaison, entre des nombres entiers. Il est facile de ramener le problème à deux entiers positifs, et on se restreint à ce cas.

Les algorithmes décrits ci-dessous calculent le quotient de la division euclidienne ; il est bien clair que le reste s'en déduit. Attention, le contraire ne serait pas vrai.

La première méthode, naturelle mais naïve, demande beaucoup trop de calculs pour des grands nombres. On présente ensuite deux méthodes courantes, de complexité semblable : la première convient pour des calculs en base 2, et donc pour une programmation informatique ; la deuxième méthode, essentiellement équivalente, est une adaptation pour la base de numération habituelle, la base décimale, et convient donc pour des calculs à la main. C'est l'algorithme enseigné à l'école.

Méthode naïve

Pour effectuer la division euclidienne de a par b, on construit une suite arithmétique strictement décroissante (a_i) de raison (-b) : a₀ = a, puis . Il existe donc un plus petit entier I tel que a_I < b : c'est-à-dire , ce qui s'écrit encore . Le quotient de la division cherchée est donc I, et le reste .

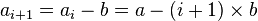
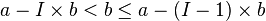
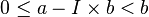
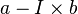
Le nombre de pas de cet algorithme est donc I c'est à dire la partie entière de ; chaque étape requiert une soustraction et une comparaison ; la complexité de calcul croît linéairement avec a, c'est-à-dire exponentiellement avec la taille de a - si on convient de mesurer la taille d'un entier par le nombre de chiffres que requiert son développement binaire (ou décimal si on préfère, cela ne modifie les choses que d'une constante), cette taille est de l'ordre du logarithme de l'entier.

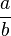
Méthode courante, binaire

Une simple amélioration consiste à faire une recherche dichotomique, sur le quotient : au lieu de parcourir comme précédemment tous les entiers depuis 0 en attendant de tomber sur le bon quotient, on va commencer par trouver rapidement un entier dont on sera sûr qu'il est plus grand que le quotient cherché ; dans la liste finie de quotients possibles restants, on fera une recherche dichotomique.

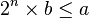
Le premier calcul se fait simplement en considérant la suite géométrique 2ⁿ. Tant que , on incrémente n de 1 à chaque étape. Soit N le plus petit entier tel que . Le nombre d'étapes pour trouver cet entier est de l'ordre de . Chacune de ces étapes ne demande qu'une multiplication par deux (encore plus facile qu'une addition, pour une écriture binaire), et une comparaison.

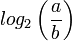
Pour le deuxième calcul, on construit deux suites (α_n) et (β_n) ; l'une stockera des minorants du quotient cherché, l'autre des majorants stricts. On pose donc α₀ = 2^{N − 1} et β₀ = 2^N, puis par récurrence :

si , alors on peut affiner le minorant, et on pose donc et

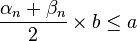
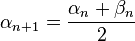
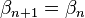
en revanche, si , on peut affiner le majorant, et on pose , et .

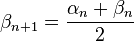
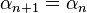
On montre facilement par récurrence qu'à chaque étape n de ce deuxième calcul, α_n et β_n sont deux entiers, tous deux multiples de 2^{N − 1 − n} et dont la différence vaut 2^{N − 1 − n} ; cette remarque permet notamment de montrer que les suites sont bien définies jusqu'à n = N − 1, et que α_{N − 1} et β_{N − 1} ne diffèrent que de 1 ; puisqu'ils sont respectivement un minorant large et un majorant strict du quotient, α_{N − 1}est le quotient cherché.

Le nombre maximal d'étapes pour ce calcul est de l'ordre de (une des dichotomies a pu donner le bon quotient avant la N - 1^ème étape, c'est le cas d'égalité de la comparaison, auquel cas on peut arrêter l'algorithme avant), qui chacune n'exige qu'une addition, une division par deux (facile en écriture binaire, ce n'est évidemment pas une division euclidienne cachée), une multiplication (qui peut être évitée, en gérant plus de variables), et une comparaison.

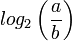
En concaténant les résultats des deux calculs, on voit que cet algorithme a une complexité qui croît logarithmiquement avec , et donc linéairement avec la taille de a . L'amélioration est donc très nette.

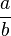
Méthode courante, décimale

Soit deux entiers naturels a et dont on veut effectuer la division. On commence par trouver la plus petite puissance de 10 telle que  ; d'après le théorème de division euclidienne, il existe alors un unique entier tel que : . On se ramène donc à faire la division de par b ; l'inégalité précédente montre que la première puissance de 10 telle que excèdera sera strictement plus petite que  ; on la note . On construit ainsi une suite d'entiers naturels (N_i) strictement décroissante ; elle vaut donc 0 à un certain rang ; on construit la suite d'entiers associée de la même façonqu'on a construit q₁. Le quotient cherché sera  : en effet l'inégalité qui donne q_r pour la première occurrence de N_r = 0 sera : , ce qui est bien la définition du quotient.

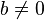
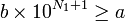
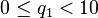
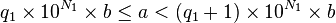
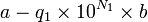
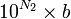
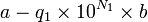
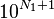
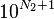
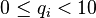
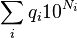
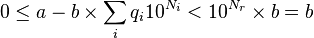
On remarque que cette méthode se divise comme la précédente en deux étapes : d'abord une recherche d'une puissance assez grande, ce qui demande à nouveau un nombre de calcul logarithmique en a, c'est-à-dire linéaire en la taille de a ; ensuite un calcul de tous les coefficients q_i associés au différentes puissances de 10 inférieures à la puissance assez grande obtenue. Pour chaque calcul de q_i, l'algorithme demande en fait un calcul de division euclidienne intermédiaire ; mais le quotient est à chercher seulement parmi les entiers de 0 à 9 ; il se fait donc rapidement en utilisant des tables.

Cette méthode est celle utilisée en primaire lorqu'il s'agit de poser une division.

Dans d'autres anneaux