Division d'un polynôme - Définition
La liste des auteurs de cet article est disponible ici.
Division selon les puissances croissantes
Théorème et définition
L'analyse utilise aussi une autre division, dite selon les puissances croissantes. Elle joue un double rôle, pour les fonctions rationnelles et les développements limités. Intégrer une fonction rationnelle est aisée une fois qu'elle est décomposée en éléments simples. L'algorithme de décomposition fait appel à la division selon les puissances croissantes. Pour calculer le développement limité d'une fonction, s'exprimant sous forme de fraction, la méthode la plus simple est parfois de calculer le développement limité du numérateur et du dénominateur. La division selon les puissances croissantes offre un développement limité de la fraction.
Le théorème établissant l'existence et l'unicité de cette division est un peu analogue au précédent, sur la division euclidienne :
Théorème de la division selon les puissances croissantes — Soient A et B deux polynômes à coefficients dans K. On suppose que le terme constant de B n'est pas nul et on note p un entier supérieur ou égal au degré de B. Il existe un unique couple de polynômes (Q, R) tel que A soit égal à B.Q + Xp+1.R et tel que le degré de Q soit inférieur ou égal à p.
Le vocabulaire est le même que celui de la division euclidienne, on parle encore d'identité de la division selon les puissances croissantes, de quotient et de reste.
La démonstration est analogue à la précédente :
-
- Le couple (Q, R), s'il existe, est unique :
On suppose l'existence de deux couples (Q1, R1), (Q2, R2) résultat de la division selon les puissances croissantes de A par B, on va montrer qu'ils sont égaux. On dispose des égalités :
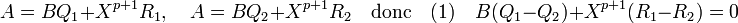
Le polynôme Xp+1(R1 - R2) ne contient aucun terme de degré strictement inférieur à p + 1. Comme Q1 et Q2 sont de degrés inférieurs ou égaux à p leur différence est un polynôme de degré inférieur ou égal à p. Comme B contient un terme constant, si Q1 - Q2 n'est pas nul, B.(Q1 - Q2) est un polynôme contenant au moins un monôme non nul de degré inférieur ou égal à p. Ce monôme ne peut être annulé par le polynôme Xp+1(R1 + R2) car tous ses monômes sont au moins de degré p + 1. On en déduit que Q1 est égal à Q2 et, par conséquent que R1 est égal à R2.
-
- Il existe un couple (Q, R) satisfaisant l'identité de la division euclidienne :
Cette fois ci, il est plus simple de voir les polynômes A et B dans l'autre sens, avec n désignant le maximum des degrés de A et de B :
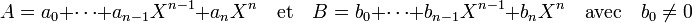
On raisonne encore une fois par récurrence sur p. Si p est égal à 0 :
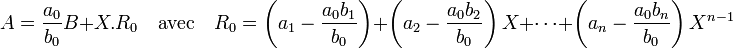
Le degré de Q est moins l'infini si a0 est nul, soit nul sinon. Il est toujours inférieur ou égal à 0, la valeur de p.
On suppose maintenant le résultat vrai pour toute valeur inférieure ou égale à p et montrons le à l'ordre p + 1. L'hypothèse de récurrence montre l'existence d'un polynôme Rp tel que :
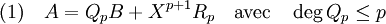
Il est encore possible d'appliquer la division selon les puissances croissantes à l'ordre 0 sur Rp :
![\exists \lambda_p \in \mathbb K,\; \exists R_{p+1} \in \mathbb K[X] \quad (2)\quad R_p = \lambda_pB + XR_{p+1}](https://static.techno-science.net/illustration/Definitions/autres/1/1bef33b7acf9d25f1fe23b9242b406e9_dbc286ad8e5cd02e78cb4813439f6808.png)
En remplaçant la valeur de Rp dans l'égalité (1), on obtient :
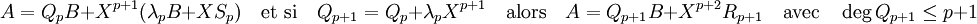
Ce qui établit la proposition.
Exemple et algorithme
La méthode de calcul est exactement la même que celle du paragraphe précédent, il suffit d'ordonner le polynôme dans le sens inverse. Illustrons le avec les polynômes suivants :
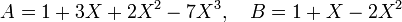
On obtient, si p est égal à 3 :
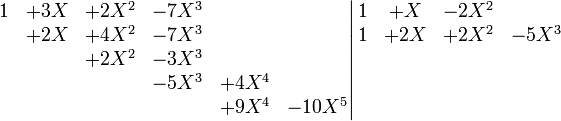
Ce qui s'écrit :