Division d'un polynôme - Définition

Anneau commutatif unitaire intègre

Absence de division euclidienne

La démonstration de l'existence d'une division euclidienne dans un anneau de polynômes utilise le fait que le coefficient du monôme dominant (celui de plus haut degré) est inversible pour la multiplication. Une question naturelle est celle de l'existence d'une division euclidienne pour l'ensemble des polynômes à coefficients dans un anneau commutatif unitaire intègre comme par exemple celui des entiers. Un anneau est à l'image d'un corps, mais une propriété est manquante. Tous les éléments ne sont pas inversibles pour la multiplication, comme par exemple 2 pour les entiers. On suppose toutefois que l'anneau est intègre, c'est-à-dire que si le produit de deux éléments a.b est nul, alors soit a soit b est nul. On suppose aussi qu'il est unitaire, c'est-à-dire qu'il existe un élément neutre pour la multiplication. Ici A désigne un anneau commutatif unitaire intègre, si le lecteur n'est pas familier avec ce vocabulaire, il peut imaginer que A est soit Z, l'ensemble des entiers et les polynôme sont à coefficients entiers, soit A désigne R[Y], l'anneau des polynômes en une indéterminée Y et A[X] désigne l'anneau des polynômes en deux indéterminées à coefficients réels R[X,Y].

Pour démontrer l'absence d'une division euclidienne, on peut remarquer que son existence impose de nombreuses conséquences arithmétiques sur la structure de l'ensemble (cf l'article Anneau euclidien). Ainsi, un ensemble de polynômes qui possède une division euclidienne, pas nécessairement construit sur le degré du polynôme, vérifie toujours l'identité de Bézout. Ceci signifie que si A et B sont deux polynômes qui n'ont aucun autres facteurs communs que les éléments inversibles de l'anneau, il existe deux polynômes M et N tel que AM + BN soit égal à 1. L'existence de l'élément a montre un contre exemple à l'identité de Bézout.

On considère les deux polynômes X et le polynôme constant a. Le polynôme X est irréductible, c'est-à-dire qu'il n'admet aucun diviseur autre que les éléments inversibles de l'anneau et le produit d'un élément inversible et de lui-même. Les hypothèses de l'identité de Bézout sont bien vérifiées. On considère M et N deux polynômes à coefficients dans A et le produit P égal à aM + XN. Pour que ce P soit égal à 1, N est nécessairement égal au polynôme nul, sinon P est de degré supérieur ou égal à 1. Or, quelle que soit la valeur de M, le produit aM n'est pas égal à 1 car a n'est pas inversible. L'identité de Bézout n'est jamais vérifiée, ce qui montre l'absence de toute division euclidienne dans A[X].

Palliatifs

L'analyse de la démonstration de l'existence d'une division euclidienne montre que si M est un polynôme à coefficients dans A et si son monôme dominant possède un coefficient inversible, la division est possible. Ce qui signifie que quel que soit N, il existe unique un couple (Q, R) satisfaisant à l'identité de la division euclidienne de N par M.

Dans le cas général, il existe encore un résultat qui s'applique :

Proposition — Soit M et N deux polynômes à coefficients dans A. Il existe un élément λ de A et un unique couple (Q, R) satisfaisant à l'identité de la division euclidienne de λ.N par M :

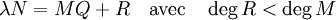
Pour le démontrer, on construit K le corps des fractions de A, exactement comme on construit le corps des nombres rationnels sur l'anneau des entiers ou le corps des fractions rationnelles sur les polynômes. Les polynômes M et N peuvent aussi être vus comme des polynômes à coefficients dans K, de la même manière qu'un polynôme à coefficients entiers peut être aussi vu comme un polynôme à coefficients rationnels. Dans K[X], la division euclidienne est possible et il existe un couple Q₁ et R₁ de polynômes à coefficients dans K satisfaisant à l'identité de la division euclidienne de N par M et :

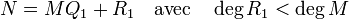
Soit λ un multiple des dénominateurs des coefficients de Q₁ et R₁, la multiplication de l'égalité précédente par λ montre que :

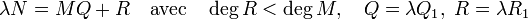
Comme λ est un multiple des dénominateurs des coefficients de Q₁ et R₁, par définition de Q et R, ce sont bien des polynômes à coefficients dans A. L'unicité est une conséquence de celle de la division euclidienne dans un anneau de polynômes à coefficients dans un corps. L'égalité de la division peut être vue comme l'identité de la division euclidienne de λN par M dans K, l'unicité de cette identité montre celle recherchée.

Remarque 1 : Attention, ce n'est pas λ qui est unique, ce sont les polynômes Q et R, une fois λ choisi.

Remarque 2 : Si A n'est pas commutatif, il existe encore certains résultats, ils sont décrits dans l'article Anneau non commutatif de polynômes.