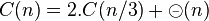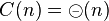Diviser pour régner (informatique) - Définition

Introduction

Diviser pour régner est une technique algorithmique consistant à diviser un problème de grande taille en plusieurs sous-problèmes analogues. L'étape de subdivision est appliquée récursivement. Son nom est inspiré du proverbe « Diviser pour régner » (en latin : « Divide ut imperes  »)

Présentation

Les algorithmes récursifs utilisent naturellement cette technique : ils s'appellent eux-mêmes une ou plusieurs fois sur une partition du problème initial et combinent les solutions pour retrouver une solution au problème initial.

Deux stratégies

Les algorithmes Diviser pour régner appliquent deux stratégies principales. La première est la récursivité sur les données : on sépare les données en deux parties quelconques (ou plus), puis on résout les sous-problèmes (par la même fonction), pour enfin combiner les résultats. La seconde stratégie, la récursivité sur le résultat, consiste elle à effectuer un pré-traitement pour bien découper les données, puis à résoudre les sous-problèmes, pour que les sous-résultats se combinent d'eux-mêmes à la fin.

Illustration des stratégies

Tri fusion

Un exemple de récursivité sur les données est le Tri fusion. La donnée initiale est alors une séquence d'entiers non triée. Le résultat est une séquence triée des mêmes entiers.

1. on divise la séquence de n éléments à trier en deux sous-séquences de n/2 éléments,
2. on trie les deux sous-séquences à l'aide du tri fusion (appel récursif),
3. on combine, en les fusionnant, les deux sous-séquences triées pour produire la séquence triée.

La récursivité prend fin quand pour un appel à l'algorithme, la séquence à trier est de taille 1. Dans ce cas il n'y a rien à faire car par définition une telle séquence est déjà triée.

Tri rapide

Un exemple de récursivité sur le résultat est le Tri rapide. La donnée initiale et le résultat sont les mêmes que pour le tri fusion.

1. on choisit un élément du tableau au hasard qui sera 'pivot'
2. on permute tous les éléments de manière à placer à gauche du pivot les éléments qui lui sont inférieurs, et à droite ceux qui lui sont supérieur
3. on appelle (récursivement) le tri rapide sur les deux moitiés de part et d'autre du pivot.

Lorsque la séquence à trier est de taille 1, il n'y a plus rien à faire, car le tableau est déjà trié.

Exemples

• la Recherche dichotomique
• le Tri fusion
• le Tri rapide
• le Parcours de Graham

Complexité

La faible complexité des algorithmes Diviser pour régner est l'un de leurs principaux intérêts.

Notations : n taille du problème, C(n) coût en nombre d'opérations. Pour les notations de comparaison asymptotiques, consulter Notations de Landau

Cas où la résolution d'un seul sous-problème suffit

Théorème

Si C(n) = C(n / k) + g(n), alors

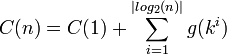
Exemple

Recherche dichotomique : avec deux comparaisons, on choisit le tableau sur lequel continuer la recherche.

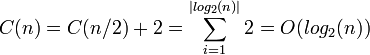
Cas des sous-problèmes de même taille

Théorème 1

Si C(n) = aC(n / b) + cn, avec C(1)=constante alors

• si a < b, C(n) = O(n)
• si a = b, C(n) = O(n.log(n))
• si a > b,

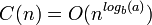
a représente ici le nombre de sous-problèmes et n/b leur taille.

Exemple 1

Tri fusion : 2 sous-problèmes de taille n/2, donc a=b=2, donc C(n) = O(n.log₂(n))

Théorème 2

Si C(n) = aC(n / k) + f(n) avec a et k deux entiers strictement positifs et f une fonction. Alors

• si avec ε > 0, alors
• si alors
• si avec ε > 0 et si tel que a.f(n / k) < = cf(n) pour n suffisamment grand, alors
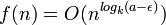
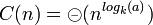
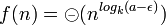
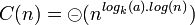
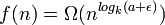
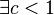
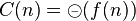
• si a=1 et f(n) = O(log_k(n)) avec k > = 1 alors C(n) = O(log_{k + 1}(n))

Exemple 2

Si , alors