Distance focale - Définition

Calcul et mesure

Il est toujours possible de calculer les distances focales à partir des données géométriques et des indices d'un système (courbure, indice de réfraction) puisqu'elles sont reliées à la vergence. Néanmoins quand ces données viennent à manquer une mesure expérimentale est possible.

Les mesures expérimentales, pour les systèmes minces tels les lentilles minces, reposent généralement sur la détermination des positions des foyers objet et image. On rappelle que le foyer image est le point vers lequel convergent après le système des rayons qui sont parallèles à l'axe optique avant le système. À l'inverse, des rayons passant par le foyer objet ressortent parallèles à l'axe optique. Les rayons ne passent pas nécessairement physiquement par le foyer, il peut s'agir de leur prolongation.

On peut en avoir l'illustration dans quelques cas simples :

• lentille optique ;
• miroir courbe.

On peut aussi la mesurer expérimentalement de plusieurs façons :

• En la mesurant directement entre la lentille et l'image nette d'un objet suffisamment lointain pour être considéré comme à l'infini (soleil, étoiles ou paysage à l'horizon).
• Avec la méthode dite de Silbermann : quand la lentille est placée de telle façon que l'image sur un écran (image réelle) a la même taille que l'objet alors la distance entre l'image et l'objet vaut quatre fois la distance focale.
• Par la méthode d'autocollimation (pour les lentilles convergentes seulement) : après avoir accolé un miroir plan à une lentille, il suffit de rechercher la position de la lentille pour laquelle objet et image se superposent parfaitement. La distance entre l'objet et la lentille est alors la distance focale de cette lentille.

Projection cinématographique

Relation entre la hauteur h du photogramme (film sur la gauche), la distance focale ƒ de l'objectif (au centre), la hauteur H de l'écran (à droite) et la distance pellicule-écran D (distance de projection)

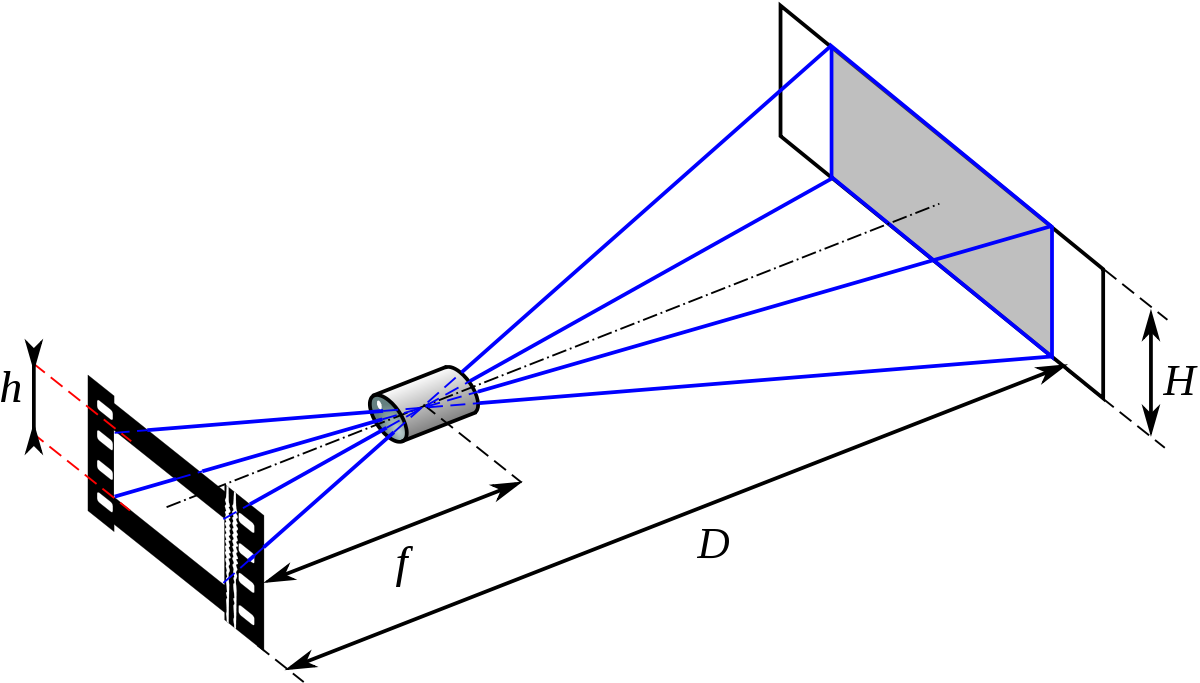
En projection cinématographique, l'écran est situé « à l'infini » et la pellicule est donc dans le plan focal. La distance focale ƒ est adaptée afin que la hauteur de l'image projetée corresponde à la hauteur de l'écran. La focale à utiliser se calcule aisément en fonction de :

1. la hauteur de l'image sur la pellicule (voir Format de projection), h ;
2. la hauteur de l'écran, H ;
3. la distance pellicule-écran, D.

Il s'agit d'une simple loi proportionnelle (théorème de Thalès) :

H/h = (D-ƒ)/ƒ

or ƒ << D, donc :

H/h ~ D/ƒ

finalement :

f ~ D*h/H.

Sur la pellicule, la largeur du photogramme est constante (18 mm), mais à la projection, c'est la hauteur qui est constante (hauteur de l'écran) ; on utilise donc des objectifs avec différentes focales ; pour le format 2,35:1 (CinemaScope), on utilise de plus une anamorphose

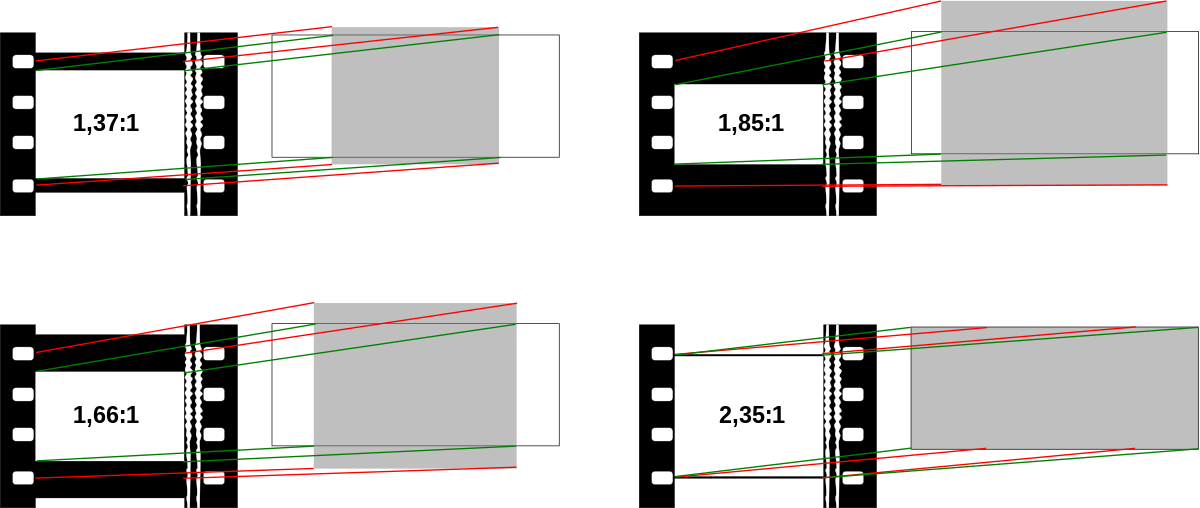
On utilise un cache pour tronquer la fenêtre de projection :

• en général, une bande noire remplit ce rôle, mais elle n'est pas totalement opaque d'une part (pour la puissance de la lanterne), et d'autre part, comme le reste de la pellicule, elle peut être endommagée et laisser passer de la lumière ;
• certains films contiennent une image plus grande que celle projetée (l'image impresionnée lors de la prise de vue est plus haute que le cadre), donc pas de bande noire.

Dans le cas du CinemaScope (rapport largeur sur hauteur de 2,35), on utilise une anamorphose : un complément optique afocal placé devant l'objectif de prise de vue ou parfois dans le système de tirage des copies comprime l'image dans le sens de la largeur sur la pellicule ; ce même dispositif est utilisé devant l'objectif de projection pour restituer, sur l'écran, une image remise à sa bonne largeur. Le plus connu de ces dispositifs est l'Hypergonar du professeur Chrétien mais il en existe d'autres ; tous comportent des associations de « lentilles » cylindriques.