Dislocation - Définition

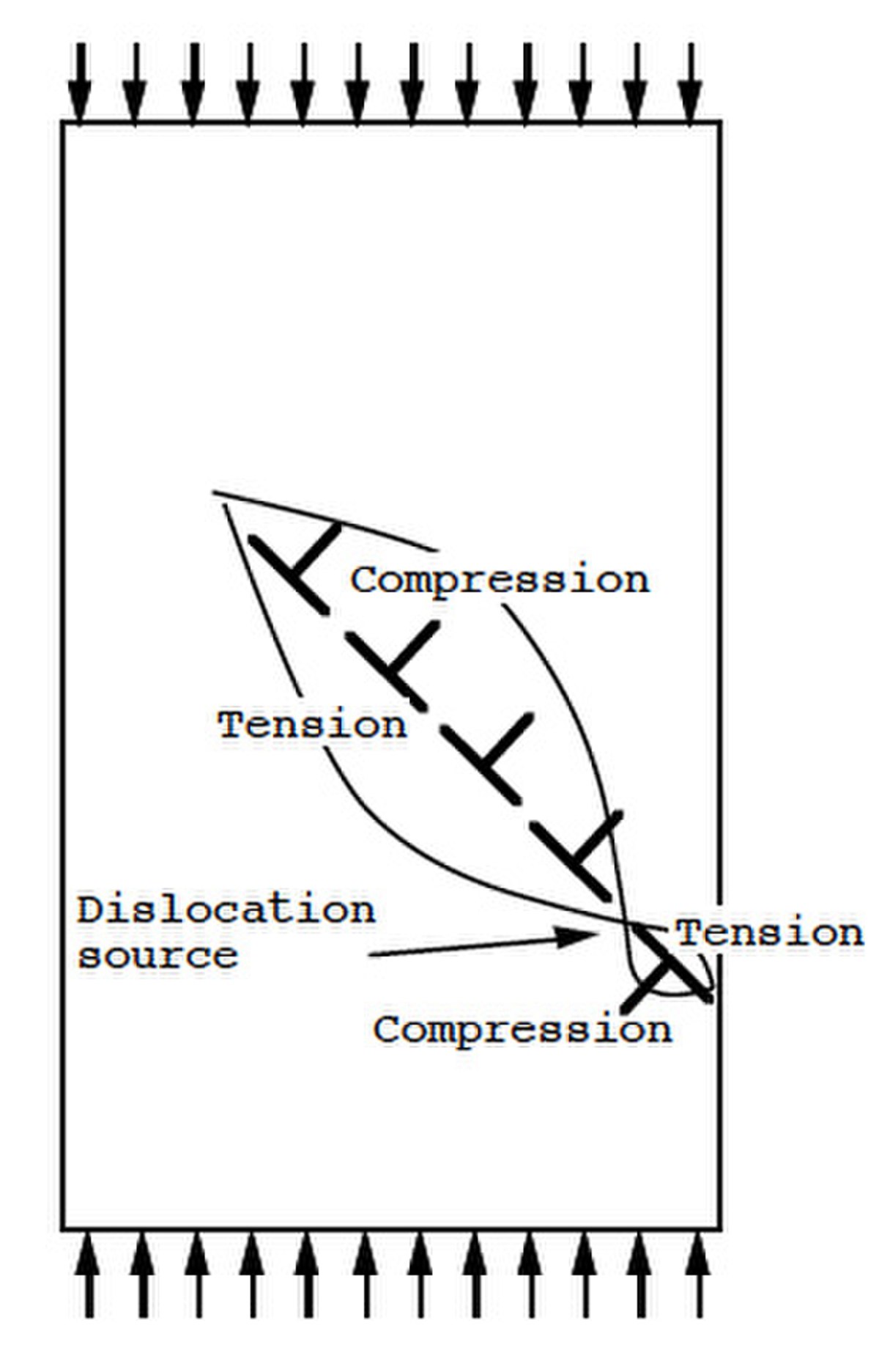
Arrangement de dislocations

Source de dislocations

Visualisation du champ de contraintes d'un empilement de dislocations par photoélasticité.

Empilement de dislocations dans un cristal de fluorure de lithium déformé par compression verticale. Les compressions, parallèles au plan de glissement, sont en vert et les tractions en rouge.

Le point d'inversion des couleurs correspond à un changement de signe des dislocations coin, c'est-à-dire à une source de dislocations coin. Le vecteur de Burgers des dislocations est incliné à 45°. Les dislocations individuelles peuvent être observées grâce aux figures d'attaque qui se traduisent par des petites pyramides à la surface du cristal le long du plan de glissement.

La largeur de l'éprouvette est de quelques millimètres et le nombre total de dislocations dans le plan de glissement de quelques milliers. Le cristal de LiF étant un cristal ionique analogue au sel NaCl, on observe des charges électriques négatives sur la source et positives à l'intersection du plan de glissement et de la surface.

En général, il y a de nombreux plans de glissement. Il est exceptionnel de n'en avoir qu'un seul comme sur la photo.

Propriétés des dislocations

Vecteur de Burgers

Le vecteur de Burgers se définit comme étant le vecteur nécessaire à boucler un circuit initialement fermé dans le cristal parfait et qui se trouve ouvert lorsqu'il enlace la ligne de dislocation. Ce vecteur n'est pas quelconque dans un cristal mais représente une translation du réseau. Par exemple dans l'aluminium cubique faces centrées, le vecteur de Burgers traditionnellement rencontré est b= a/2 [110], de norme |b|= 0.29 nm. En termes plus mathématiques, il s'agit de l'intégrale du déplacement sur un circuit fermé enlaçant la ligne de dislocation u : b= int du

Physiquement, le vecteur de Burgers représente l'amplitude de la déformation transportée par une dislocation. Comme les dislocations sont des objets flexibles, deux dislocations peuvent interagir pour former une troisième dislocation si et seulement si la quantité de déformation est conservée : on parle de jonction attractive. Il s'ensuit qu'à un nœud entre plusieurs dislocations, la somme des vecteurs de Burgers est nulle (analogue de la loi de Kirchhoff).

Champ de contrainte élastique

Comme une dislocation isolée est une singularité élastique, elle développe un champ de contrainte à longue distance, de la même façon qu'un électron est entouré d'un champ électromagnétique de portée infinie. Dans le cas d'une dislocation vis, il est de la forme : (il s'agit en réalité d'un tenseur dont les seules composantes non nulles correspondent à des cisaillements purs dans les plans radiaux parallèles à u et dans les plans horizontaux perpendiculaires à un rayon autour de la dislocation)

On voit qu’il est proportionnel au vecteur de Burgers (ce qui est analogue à la charge électrique), au module de cisaillement (analogue à la permittivité électrique du milieu), et inversement proportionnel à la distance. Ainsi, une dislocation peut être vue comme un quantum de déformation élémentaire.

Interaction avec une contrainte extérieure

Comme les dislocations possèdent un champ élastique, elles peuvent interagir avec un champ extérieur.

Interaction avec une autre dislocation

Interaction avec le réseau

Le réseau cristallin étant périodique, il y a des positions où la dislocation a une énergie élastique plus importante que d'autres. Le déplacement de la dislocation nécessite de vaincre ces « barrières énergétiques » ; on a donc un phénomène similaire au frottement. Cette force de frottement induite est appelée « force de Peierls-Nabarro ».

De fait, lorsqu'un métal subit une déformation plastique, il s'échauffe.

Interaction avec des défauts ponctuels

Les dislocations attirent les atomes ne faisant pas partie du réseau (atomes étrangers : impuretés ou éléments d'alliage). Si ces atomes étrangers sont mobiles, ils migrent vers les dislocations et constituent un « nuage de Cottrell ». Ce nuage de Cottrell gêne le mouvement des dislocations, ceci explique que les métaux purs sont plus ductiles que les métaux alliés.

Lorsque la force de déformation (la contrainte) est suffisante pour arracher la dislocation à son nuage, la mobilité augmente subitement ; ceci explique le décrochement observé parfois sur les courbes de traction (voir l'article Essai mécanique).

Si les atomes sont mobiles (température suffisante pour permettre la diffusion) et que la dislocation ne bouge pas trop vite (vitesse de déformation modérée), les atomes peuvent rejoindre la dislocation et l'épingler à nouveau. On constate donc des oscillations sur la courbe de traction, c'est le « phénomène de Portevin-Lechatelier ».

Lorsque la dislocation est fortement épinglée sur des atomes immobiles, seule la partie centrale va bouger, elle va donc se courber. Si elle se courbe jusqu'à ce que ses branches se touchent, il se forme une dislocation circulaire qui va bouger librement. On a ainsi un phénomène de multiplication des dislocations, le « mécanisme de Frank et Read », qui explique l'écrouissage.

Dislocation et polycristal

Dépendance de la limite élastique avec la taille de cristallite.

Interaction avec des précipités

Deux cas différents peuvent se produire lorsqu'une dislocation rencontre un précipité et tente donc de le cisailler pour passer au-travers:

1. Le précipité est suffisamment petit pour pouvoir être cisaillé par la dislocation. Cependant, le précipité va exercer une force de rappel sur la dislocation qui tente de le cisailler en se déplaçant et cette force sera d'autant plus grande que le précipité est gros. Cette force est notamment due au champ de contraintes entourant le précipité du fait de sa non-homogénité avec la matrice. De ce fait, la dislocation aura de plus en plus de mal à progresser et se déformera de plus en plus. Au plus difficilement la dislocation passera à travers le précipité, au plus dur sera le matériau concerné puisque c'est justement la difficulté de mouvement des dislocations au sein d'un matériau qui est responsable de sa dureté.
2. Le précipité est trop gros que pour que la dislocation puisse le cisailler. Dans ce cas, la dislocation va se refermer de plus en plus sur elle-même en tentant de cisailler et contourner le précipité jusqu'à se refermer totalement, formant ainsi une nouvelle ligne de dislocation devant le précipité tout en laissant une petite dislocation autour du précipité: c'est ce qu'on appelle le mécanisme d'Orowan et c'est un des mécanismes de multiplication des dislocations. Dans ce cas-ci, la dureté de l'échantillon va diminuer avec la taille du précipité.

En résumé, on peut dire que la dureté du matériau va d'abord augmenter avec la taille des précipités puis diminuer, en passant par un maximum, un pic de dureté correspondant à un état du matériau dit état T6. En général, on favorisera les échantillons comportant des précipités légèrement plus gros que ceux que l'on trouverait à l'état T6 pour éviter tout mécanisme de cisaillement, ce qui aurait pour effet de réduire la taille des précipités, et donc de réduire la dureté du matériau.

Dans le cas ou l'échantillon contient plusieurs familles de précipités de tailles différentes, deux par exemple, la dureté du matériau dépendra de la taille relative et de la position des pics de dureté correspondant à chaque famille de précipités:

Si un des deux pics est clairement plus petit que l'autre (i.e: une des deux courbes de dureté est toujours inférieure à l'autre), la dureté du matériau sera celle qui est donnée par la courbe la plus haute.

Si par contre les deux pics sont de hauteur voisine mais correspondent à différents diamètres de précipités, la dureté suivra l'enveloppe des deux courbes de dureté, c'est-à-dire qu'elle prendra le maximum des deux valeurs donnés par les courbes pour chaque diamètre de précipités. On aura alors une courbe globale de dureté divisée en 4 phases: une croissante (mécanisme de cisaillement) jusqu'au premier pic, puis décroissante (mécanisme d'Orowan) jusqu'à l'intersection des deux courbes; à nouveau croissante jusqu'au second pic et enfin une deuxième fois décroissante.