Discriminant - Définition

Introduction

Incidence du signe du discriminant sur les racines de l'équation du second degré à coefficients réels.

En mathématiques, le discriminant est une notion algébrique. Il est utilisé pour résoudre des équations du second degré. Il se généralise pour des polynômes de degré quelconque et dont les coefficients sont choisis dans des ensembles équipés d'une addition et d'une multiplication. Le discriminant apporte dans ce cadre une information sur l'existence ou l'absence de racine multiple.

Le discriminant est utilisé dans d'autres domaines que celui de l'étude des polynômes. Son usage permet de mieux comprendre les coniques et les quadriques en général. On le retrouve dans l'étude des formes quadratiques ou celle des corps de nombres dans le cadre de la théorie de Galois ou celle des nombres algébriques. Sa définition se fonde sur le calcul d'un déterminant.

Polynôme du second degré

Résolution de l'équation à coefficients réels

Considérons une équation du second degré, ici a, b et c sont trois coefficients réels tel que a est différent de zéro :

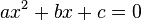
Discriminant de l'équation du deuxième degré —  Le discriminant de l'équation précédente est le nombre Δ défini par :

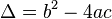
La connaissance du discriminant permet de résoudre l'équation :

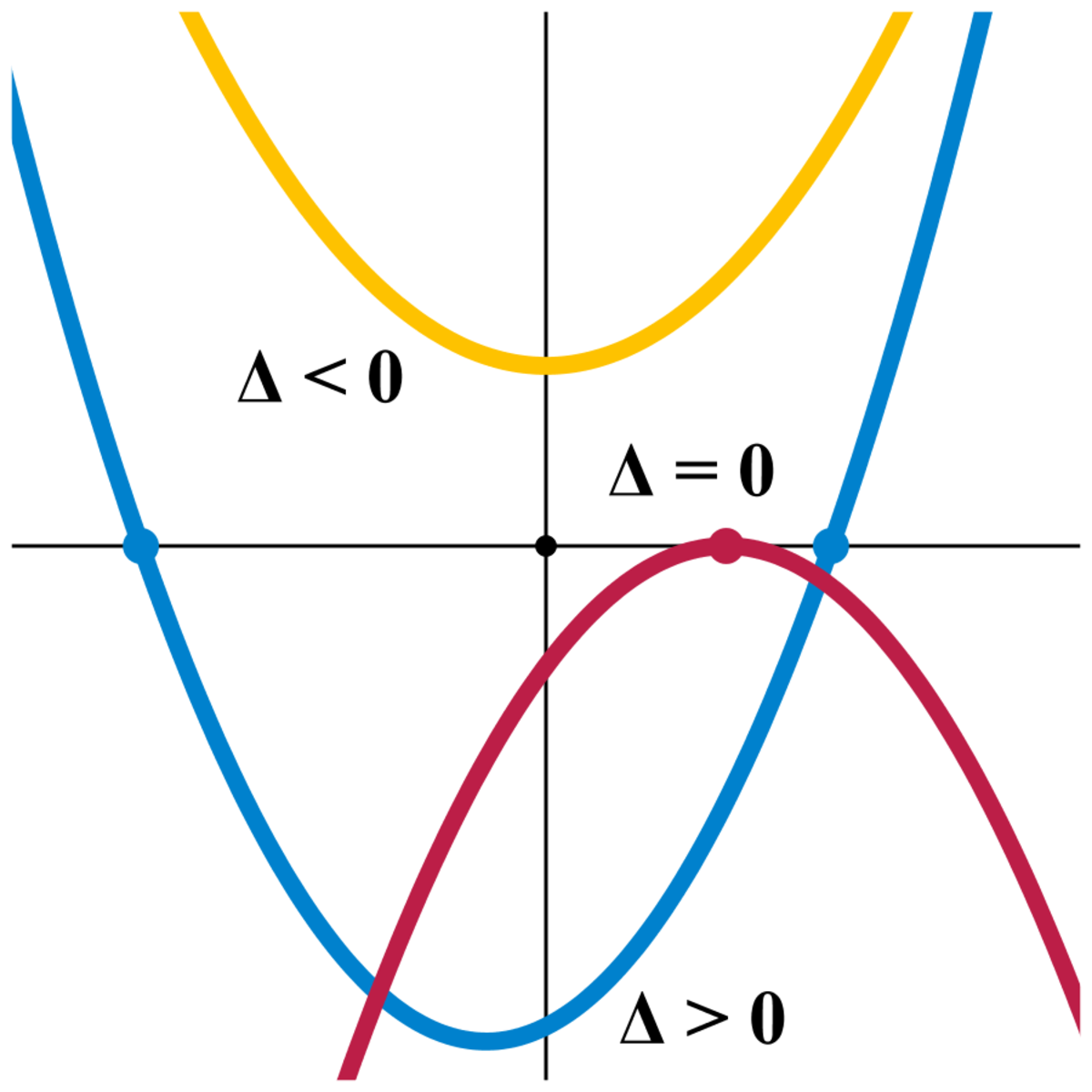
Résolution de l'équation —  Si le discriminant est strictement positif, l'équation admet deux solutions x₁ et x₂ données par les formules suivantes :

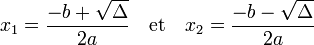
Si le discriminant est nul, l'équation admet une racine double :

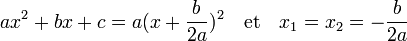
Si le discriminant est strictement négatif, l'équation n'admet pas de solution réelle.

Résolution de l'équation à coefficients complexes

Si les coefficients a, b et c sont complexes ou si les solutions complexes de l'équation sont admises, la situation est un peu différente. Le théorème de d'Alembert-Gauss précise qu'il existe toujours au moins une solution à l'équation. Dans l'ensemble des complexes, un nombre admet toujours deux racines carrées, il existe une valeur δ tel que son carré δ² soit égal à Δ :

Racines complexes —  Si le discriminant est différent de zéro, l'équation admet deux solutions x₁ et x₂ données par les formules suivantes :

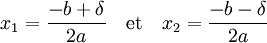
Si le discriminant est nul, l'équation admet une racine double égal à -b / 2a.

Discriminant réduit

Si on écrit l'équation du second degré sous la forme suivante :

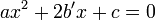
Il devient plus simple d'utiliser une autre expression :

Discriminant réduit —  Le discriminant réduit de l'équation précédente est le nombre Δ' défini par :

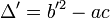
L'expression des racines, si elles existent, devient :

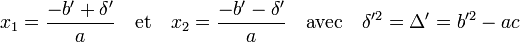
Exemples

Cherchons à résoudre l'équation suivante :

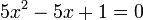
Le calcul du discriminant Δ et des racines x₁ et x₂ donne :

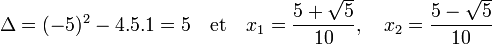
Dans le cas de l'équation suivante, on remarque que le discriminant réduit est nul, il n'existe qu'une racine égale à -3.

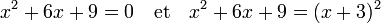
Le dernier exemple décrit une situation où le discriminant est strictement négatif, ici égal à -3. On remarque de i√3 est une racine carrée du discriminant, si i désigne l'unité imaginaire. Ce qui permet de déterminer les solutions :

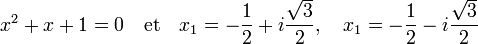
On peut remarquer que ces deux racines sont des racines de l'unité. A la puissance trois, ces racines ont pour valeur un. Le polynôme choisi est un cas particulier de polynôme cyclotomique.

Forme quadratique en dimension deux

Si le discriminant de la forme quadratique est négatif, l'ensemble des points de R² défini par φ(x, y) = a est une hyperbole. Si a est positif, on obtient une courbe analogue à celle en bleu, si a est négatif en vert. Si a est égal à zéro l'hyperbole est dégénérée, on obtient la figure rouge.

Sur l'ensemble des nombres réels, une forme quadratique φ en dimension deux associe à deux variables x et y un nombre à l'aide de la formule suivante :

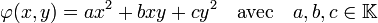
Une forme quadratique possède aussi une expression matricielle :

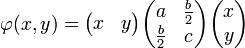
Le déterminant de l'expression matricielle est égal à -1/4(b² - 4ac), on retrouve une expression proche de la précédente. Un changement de base, à l'aide d'une matrice de passage P modifie la valeur du déterminant. Plus exactement la valeur dans la nouvelle base est égale à la valeur dans l'ancienne base que multiplie le carré du déterminant de P, le signe du déterminant reste invariant. Cette propriété est analysée dans l'article détaillé.

Pour cette raison, il existe trois définitions différentes du discriminant d'une forme quadratique en dimension deux. Le discriminant d'une forme quadratique dans une base B est le déterminant de la matrice associée à la forme quadratique dans la base B. L'analogie avec la situation précédente permet de définir le discriminant de la forme quadratique comme étant égal à b² - 4ac. Enfin, comme le seul invariant associé au déterminant de la forme quadratique, le discriminant est aussi défini comme le signe du déterminant qui peut prendre les valeurs +1, 0 ou -1.

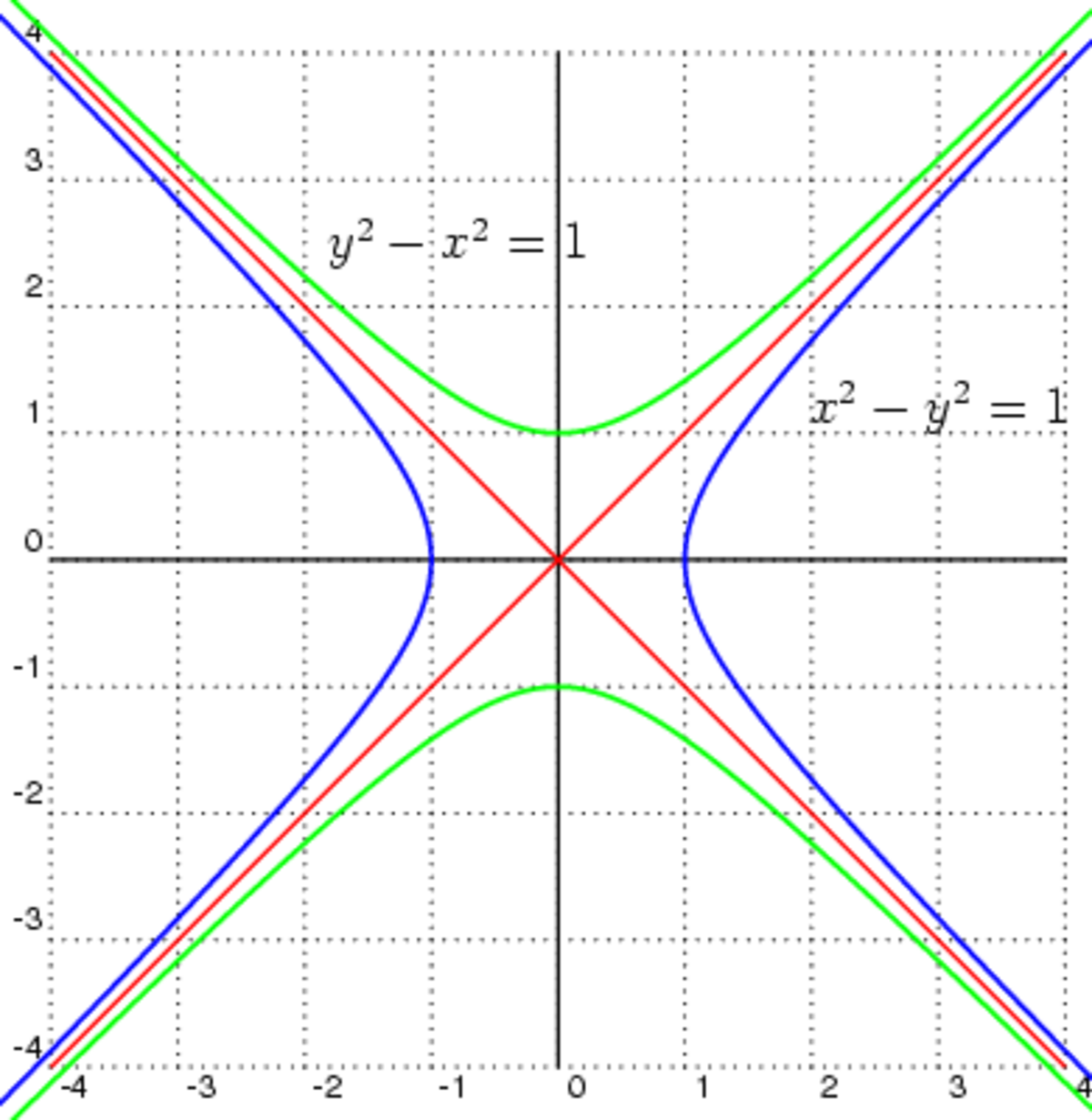
Le discriminant sépare les formes quadratiques en trois familles. En dimension deux, avec pour définition du discriminant la valeur du déterminant dans la base canonique, si le discriminant est de signe positif pour une valeur a donnée l'ensemble E_a des points (x, y) vérifiant φ(x, y) = a correspond à une ellipse ou à l'ensemble vide. Si le discriminant est nul, alors l'ensemble E_a correspond à une parabole. Si le discriminant est négatif, E_a est une hyperbole. Les formes quadratiques permettent ainsi d'obtenir les trois différentes formes de coniques.