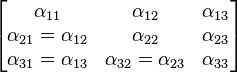Dilatation thermique - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La dilatation thermique est l'expansion à pression constante du volume d'un corps occasionné par son réchauffement, généralement imperceptible. Dans le cas d'un gaz, il y a dilatation à pression constante ou maintien du volume et augmentation de la pression lorsque la température augmente.
Origine de la dilatation thermique
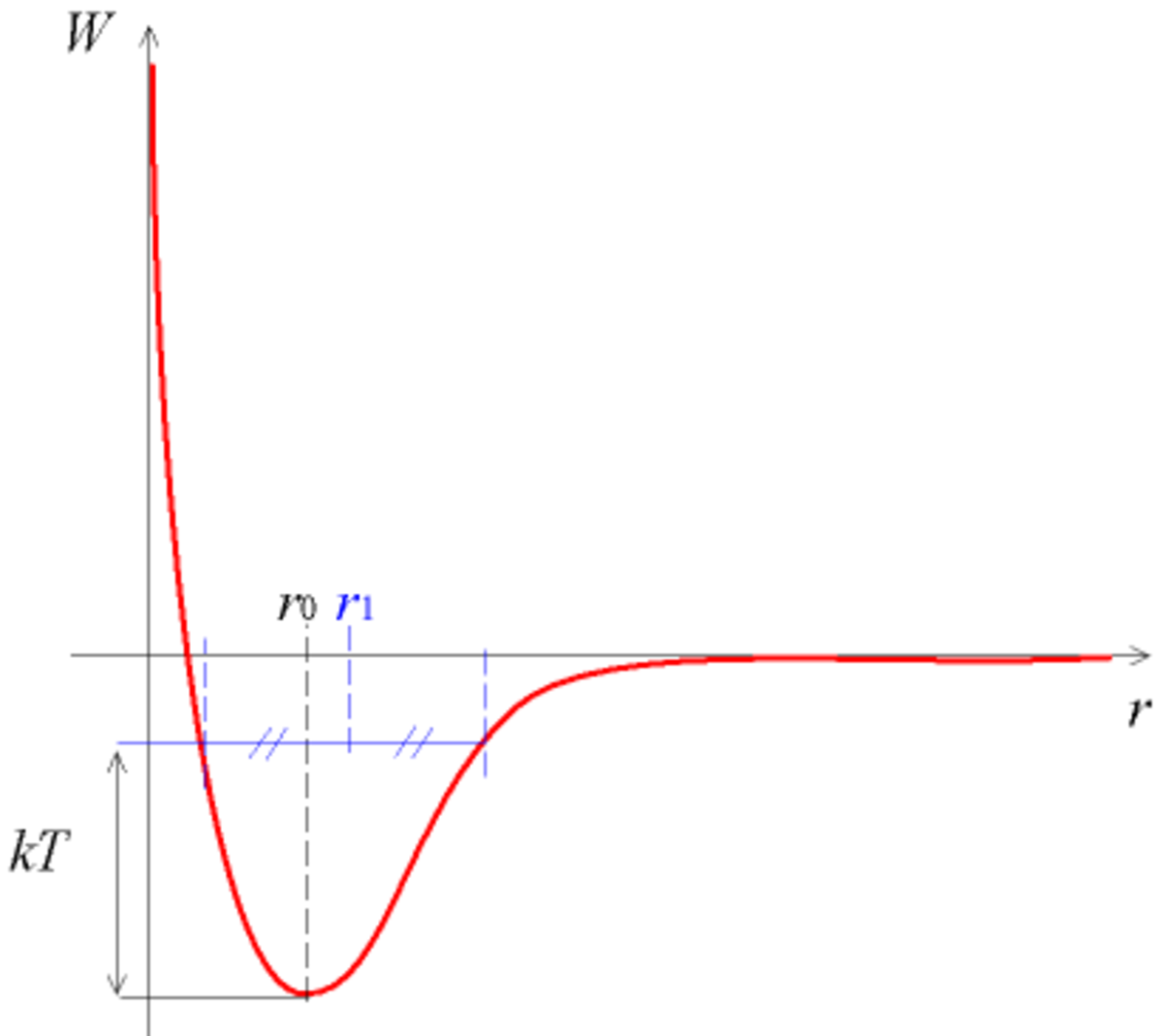
Dans un solide, les atomes possèdent une énergie thermique et vibrent autour de leur position moyenne. Cette vibration dépend de la température mais aussi du voisinage des atomes, plus précisément du potentiel créé par les atomes environnants. À basse température, les potentiels interatomiques peuvent être décrits de façon harmonique : pour des températures proches de T = 0 K, les atomes restent centrés sur leur position moyenne r0. Ce n'est plus le cas pour des températures élevées : l'anharmonicité des potentiels interatomiques introduit une dépendance de la position moyenne des atomes avec la température, ce qui cause le phénomène de dilatation thermique.
Lorsqu'un gaz est soumis à un réchauffement, la quantité de mouvement des particules qui le composent augmente. À volume constant, cela se traduit par une augmentation de la pression, car le nombre de chocs entre particules par unité de surface augmente. Si la pression doit rester constante, le volume du gaz doit alors augmenter, selon la loi des gaz parfaits. Pour les gaz non parfaits, les forces d'attraction entre les particules du gaz peuvent réduire l'expansion thermique.
La dilatation thermique des liquides a en principe les mêmes causes que celle des gaz, mais l'effet des forces d'attraction entre les particules sur la dilatation est nettement réduit, car elles sont plus proches les unes des autres.
Coefficients de dilatation thermique α
Cas isotrope
On peut calculer pour tous les matériaux isotropes la variation de longueur et donc de volume en fonction de la variation de température :
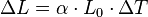
avec :
- ΔL la variation de longueur en mètre (m) ;
- α le coefficient de dilatation linéaire en kelvin puissance moins un (K -1) ;
- L0 la longueur initiale en mètre (m) ;
- ΔT = T - T0 la variation de température en kelvin (K) ou en degré Celsius (°C).
Remarque : puisqu'on utilise une variation (une différence de température) la différence d'origine entre kelvin et degré Celsius s'annule, la distinction n'est donc pas nécessaire.
On peut aussi directement calculer la longueur en fonction de la température :
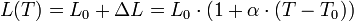
avec :
- L(T) la longueur en mètre (m) en fonction de la température ;
- T la température considérée en kelvin (K) ou en degré Celsius (°C) ;
- T0 la température initiale en kelvin (K) ou en degré Celsius (°C).
Application
Soit un rail en acier de 30 m en hiver à -20 °C ; en été, la température est de 40 °C. Le rail subit donc une variation de température ΔT = 60 K, sa variation de longueur sera :
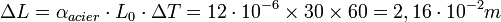
Ainsi le rail s'allonge de 21,6 mm, sa longueur en été est de 30,0216 m.
Tenseur de dilatation thermique
Les matériaux cristallins non cubiques présentent une dilatation thermique anisotrope : on n'observe pas le même coefficient de dilatation α dans toutes les directions. Pour cette raison, on utilise un tenseur symétrique d'ordre 2 pour décrire la dilatation dans les matériaux anisotropes :
Ainsi, dans le cas général d'un matériau triclinique, six coefficients de dilatation thermique sont nécessaires. Ces coefficients se rapportant à un repère orthogonal, les coefficients de dilatation n'ont pas forcément de rapport direct avec les axes cristallographiques du matériau. En effet, les valeurs propres et vecteurs propres d'un tenseur d'ordre 2 forment toujours (dans le cas où les valeurs propres sont positives) une ellipsoïde de révolution, dont les axes sont perpendiculaires les uns aux autres : on dit qu'un tenseur d'ordre 2 possède toujours au moins la symétrie ponctuelle orthorhombique maximale 2/m 2/m 2/m.
Pour un cristal orthorhombique par exemple, où α12 = α13 = α23 = 0, le tenseur de dilatation est diagonal et α11, α22 et α33 décrivent la dilatation le long des trois directions cristallographiques a, b et c du matériau. Par contre, dans le système monoclinique, α13 est non nul : alors que α22 représente la dilatation thermique le long de b, la relation entre α11, α33, α13 et les paramètres de maille a, c, β n'est pas aussi triviale. Par convention, le repère orthogonal (e1, e2, e3) choisi pour décrire la dilatation thermique dans les matériaux monocliniques est tel que e2 est parallèle au vecteur b, axe de symétrie du cristal, e3 est parallèle à c et e1 est parallèle au vecteur du réseau réciproque a*, qui forme par définition un trièdre direct avec b et c : α33 représente la dilatation thermique le long de c, alors que α11 représente la dilatation le long du vecteur réciproque a* qui est différent de a.
Dans le cas général triclinique, il est possible de calculer les coefficients du tenseur de dilatation thermique à partir des variations en température des paramètres de maille. Dans le repère conventionnel orthogonal (e1, e2, e3), défini par e3 parallèle à c, e2 parallèle à b* et e1 étant le produit vectoriel de e2 et e3, on obtient :
![\begin{array}{rcl} \alpha_{11} & = & \displaystyle{\frac{1}{a} \frac{\mbox{d}a}{\mbox{d}T} + \frac{\mbox{d}\beta}{\mbox{d}T} \cot{\beta}}\\[3ex] \alpha_{22} & = & \displaystyle{\frac{1}{b} \frac{\mbox{d}b}{\mbox{d}T} + \frac{\mbox{d}\alpha}{\mbox{d}T} \cot{\alpha} + \frac{\mbox{d}\gamma^*}{\mbox{d}T} \cot{\gamma^*}}\\[3ex] \alpha_{33} & = & \displaystyle{\frac{1}{c} \frac{\mbox{d}c}{\mbox{d}T}}\\[3ex] \alpha_{12} & = & \displaystyle{\frac{1}{2} \cot{\gamma^*} \left( \frac{1}{a} \frac{\mbox{d}a}{\mbox{d}T} - \frac{1}{b} \frac{\mbox{d}b}{\mbox{d}T} - \frac{\mbox{d}\alpha}{\mbox{d}T} \cot{\alpha} + \frac{\mbox{d}\beta}{\mbox{d}T} \cot{\beta} \right) + \frac{1}{2} \frac{\mbox{d}\gamma^*}{\mbox{d}T}}\\[3ex] \alpha_{13} & = & \displaystyle{\frac{1}{2} \cot{\beta} \left( \frac{1}{a} \frac{\mbox{d}a}{\mbox{d}T} - \frac{1}{c} \frac{\mbox{d}c}{\mbox{d}T} \right) - \frac{1}{2} \frac{\mbox{d}\beta}{\mbox{d}T}}\\[3ex] \alpha_{23} & = & \displaystyle{\frac{1}{2} \left\{ \left( \frac{1}{a} \frac{\mbox{d}a}{\mbox{d}T} - \frac{1}{c} \frac{\mbox{d}c}{\mbox{d}T} \right) \cot{\gamma^*} \cot{\beta} + \left( \frac{1}{b} \frac{\mbox{d}b}{\mbox{d}T} - \frac{1}{c} \frac{\mbox{d}c}{\mbox{d}T} \right) \frac{\cot{\alpha}}{\sin{\gamma^*}} - \left( \frac{1}{\sin{\gamma^*}} \frac{\mbox{d}\alpha}{\mbox{d}T} + \frac{\mbox{d}\beta}{\mbox{d}T} \cot{\gamma^*} \right) \right\}} \end{array}](https://static.techno-science.net/illustration/Definitions/autres/b/b5aa6c6c744d992755b37c60dd5f846f_634f576251f2921f240eef6b51a4b4f9.png)
où a, b, c, α, β, γ sont les paramètres de maille du cristal dans le réseau direct et γ* est l'angle entre les vecteurs a* et b* du réseau réciproque.
Les valeurs propres du tenseur de dilatation thermique, ou coefficients de dilatation linéaires principaux α1, α2 et α3, permettent aussi d'obtenir le coefficient de dilatation volumique β vu plus haut, trace du tenseur : β = α1 + α2 + α3 = α11 + α22 + α33, puisque la trace d'une matrice carrée est invariante par changement de base. Pour les matériaux isotropes, on retrouve ainsi le résultat β = 3α.