Dilatation thermique - Définition
La liste des auteurs de cet article est disponible ici.
Définition thermodynamique
L'énergie interne U d'un système est une fonction d'état qui dépend de la pression p, du volume V et de la température T : U = f(p,V,T). Comme ces trois variables sont reliées par l'équation d'état du système, il est possible par exemple d'exprimer une variation infinitésimale de l'énergie interne U d'un système en fonction des variations infinitésimales du volume et de la température :
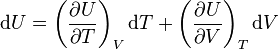
Le premier terme de la somme contient le changement de l'énergie interne en fonction de la température à volume constant, la capacité thermique isochore CV. Si le changement de température a lieu à pression constante, on obtient :
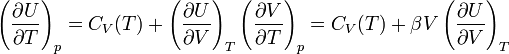
β est le coefficient de dilatation thermique isobare du système (coefficient de dilatation volumique), il décrit le changement de volume à pression constante en fonction de la température :
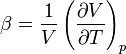
Le coefficient de dilatation volumique β est relié dans les matériaux isotropes de façon simple au coefficient de dilatation linéaire α : β = 3α. En effet, une variation de longueur infinitésimale dL = αLdT d'un cube dans les trois directions de l'espace conduit à une variation de volume dV = βVdT = 3L2dL + 3L(dL)2 + (dL)3, où les deux derniers termes sont négligeables. On obtient ainsi β = 3α.
Dans la pratique, les coefficients de dilatation thermique α et β sont souvent exprimés en fonction d'une valeur de référence pour une température déterminée T0 :
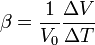
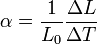
Cette formule est valable dans les cas où la variation de la longueur dépend linéairement de la variation de la température, mais pas pour de grands intervalles de température ou si le matériau subit une transition de phase dans l'intervalle considéré. De manière générale, la dépendance en température du coefficient de dilatation thermique volumique β est exprimée par la relation de Grüneisen
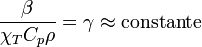
où χT est la compressibilité isotherme du matériau, Cp sa capacité thermique isochore, ρ sa densité et γ le paramètre de Grüneisen. Comme χT et ρ sont en première approximation indépendants de la température, les variations thermiques de Cp compensent celles de β.
Coefficients de dilatation linéaires pour les principaux matériaux
Les coefficients donnés ci-dessous sont valables pour des températures comprises entre 0 °C et 100 °C. En réalité ces coefficients dépendent de la température, la loi d'allongement n'est donc pas linéaire pour des différences de température très élevées.
| substances | coefficient de dilatation linéaire 1/K |
|---|---|
| acier | 12,0×10−6 |
| bronze | 17,5×10−6 |
| constantan | 15,2×10−6 |
| fonte | 10,5×10−6 |
| invar (36 %Ni + 64 %Fe) | 1,5×10−6 |
| laiton | 18,5×10−6 |
| maillechort | 18,0×10−6 |
| substances | coefficient de dilatation linéaire 1/K |
|---|---|
| nylon | 30×10−6 |
| porcelaine | 4,0×10−6 |
| quartz | 0,5×10−6 |
| rilsan | 150×10−6 |
| stéatite | 8×10−6 |
| verre sodo-calcique (verre ordinaire) | 9×10−6 |
| verre borosilicate (Pyrex) | 4×10−6 |
Coefficients d'expansion linéaire des éléments à 25 °C (×10-6 K-1) :
| H | He | ||||||||||||||||
| Li 46 | Be 11,3 | B | C | N | O | F | Ne | ||||||||||
| Na 71 | Mg 24,8 | Al 23,1 | Si 2,49 | P | S | Cl | Ar | ||||||||||
| K 83,3 | Ca 22,3 | Sc 10,2 | Ti 8,6 | V 8,4 | Cr 4,9 | Mn 21,7 | Fe 11,8 | Co 13 | Ni 13,4 | Cu 16,5 | Zn 30,2 | Ga 18 | Ge 6,1 | As | Se | Br | Kr |
| Rb | Sr 22,5 | Y 10,6 | Zr 5,7 | Nb 7,3 | Mo 4,8 | Tc | Ru 6,4 | Rh 8,2 | Pd 11,8 | Ag 18,9 | Cd 30,8 | In 32,1 | Sn 22 | Sb 11 | Te | I | Xe |
| Cs 97 | Ba 20,6 | * | Hf 5,9 | Ta 6,3 | W 4,5 | Re 6,2 | Os 5,1 | Ir 6,4 | Pt 8,8 | Au 14,2 | Hg 60,4 | Tl 29,9 | Pb 28,9 | Bi 13,4 | Po 23,5 | At | Rn |
| Fr | Ra | ** | Rf | Db | Sg | Bh | Hs | Mt | Ds | Rg | Cn | Uut | Uuq | Uup | Uuh | Uus | Uuo |
| * | La 12,1 | Ce 6,3 | Pr 6,7 | Nd 9,6 | Pm 11 | Sm 12,7 | Eu 35 | Gd 9,4 | Tb 10,3 | Dy 9,9 | Ho 11,2 | Er 12,2 | Tm 13,3 | Yb 26,3 | Lu 9,9 | ||
| ** | Ac | Th 11 | Pa | U 13,9 | Np | Pu 46,7 | Am | Cm | Bk | Cf | Es | Fm | Md | No | Lr | ||

















































