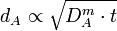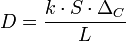Diffusion de la matière - Définition
La liste des auteurs de cet article est disponible ici.
Historique
En 1827, le botaniste Robert Brown observe le mouvement erratique de petites particules de pollen immergées dans de l'eau. Il ne s'agit pas d'un phénomène de diffusion, puisque ce qui bouge est une particule macroscopique, mais cette « marche aléatoire » (random walk), autrement appelé par le nom de son observateur « mouvement brownien », servira de modèle pour la diffusion.
En 1896, Roberts-Austen, responsable de la monnaie en Grande-Bretagne, accole une plaquette d'or à une plaquette de plomb, fait chauffer le tout et mesure la profondeur de pénétration d'un métal dans l'autre. C'est la première mesure d'un coefficient d'interdiffusion à l'état solide.
En 1855, Adolph Fick propose des lois phénoménologiques, empiriques, inspirées de la loi de Fourier pour la chaleur (établies en 1822). C'est Albert Einstein qui démontrera les lois de Fick en 1905 avec ses travaux sur la loi stochastique. En 1908, Jean Perrin, fondateur du CNRS et prix Nobel de physique, fut le premier à mesurer la trajectoire de particules soumises au mouvement brownien et confirma ainsi l'analyse théorique d'Einstein.
Mécanismes de diffusion
Diffusion dans les cristaux
Un solide cristallin est un arrangement régulier d'atomes, mais il présente des défauts. Ce sont ces défauts qui permettent la diffusion, et essentiellement les défauts ponctuels.
On distingue essentiellement deux mécanismes :
- le mécanisme lacunaire : le cristal présente des lacunes, c'est-à-dire que certains sites sont vides ; un atome voisin de la lacune peut donc sauter cette place vide et se déplacer d'une position ;
- le mécanisme interstitiel : si l'on représente les atomes comme des sphères dures, un cristal est un empilement de sphères dures et il reste de l'espace vide entre les sphères (voir l' article Empilement compact) ; un petit atome peut donc se glisser dans un de ces interstices, et sauter d'un interstice vers un interstice voisin.
Dans tous les cas, il s'agit de sauts atomiques d'une position vers une position voisine, sous l'effet de l'agitation thermique.
Mais un cristal dispose également d'autres défauts : dislocations, joints de grain et surfaces libres. La diffusion dans ces zones est plus rapide que dans la masse du cristal.
Mouvement brownien
Le déplacement de l'espèce chimique concernée peut se modéliser par le mouvement brownien comme l'a formalisé Einstein. Ceci permet de retrouver la première loi empirique de diffusion de Fick.
Applications
Considérons un solide ne contenant pas d'espèce A. À un moment donné, on met une extrémité plane du solide en contact avec un milieu contenant une concentration constante de A. A passe alors en solution dans le solide et diffuse vers l'intérieur. On a donc à chaque instant t un profil de concentration c(x,t), x étant la profondeur par rapport au plan de contact. On peut définir le front de diffusion comme étant la profondeur dA où l'on a une concentration fixée, par exemple 1/10 de la concentration de saturation Cs.
La nature brownienne du mouvement permet de conclure que le front de diffusion avance selon une loi proportionnelle à la racine carrée du temps :
Cette situation correspond par exemple au sucre dont on trempe une extrémité dans le café, ou bien à un traitement de surface d'un métal avec une phase gazeuse ou liquide (nitruration, carburation...).
En biologie
Les symboles de cette formule sont respectivement :
- D le taux de diffusion en g⋅s-1 ou mol⋅s-1 ;
- k le coefficient de diffusion (de l'espèce chimique dans le milieu donné) en m2⋅s-1 ;
- S la surface d’échanges en m2 ;
- ΔC la différence de concentration de chaque côté de la membrane en g⋅m-3 ou mol⋅m-3 ;
- L l’épaisseur de la membrane en m.