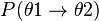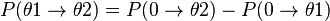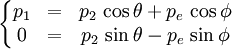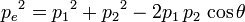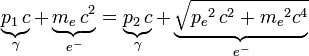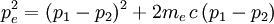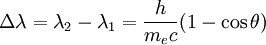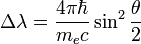Diffusion Compton - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Histoire de la découverte de l'effet Compton - Détection des photons diffusés - Démonstration - Diffusion Compton inverse

Démonstration

Schéma montrant la collision d'un photon sur un électron au repos. L'angle de diffusion du photon est

θ

, et celui de l'électron

φ

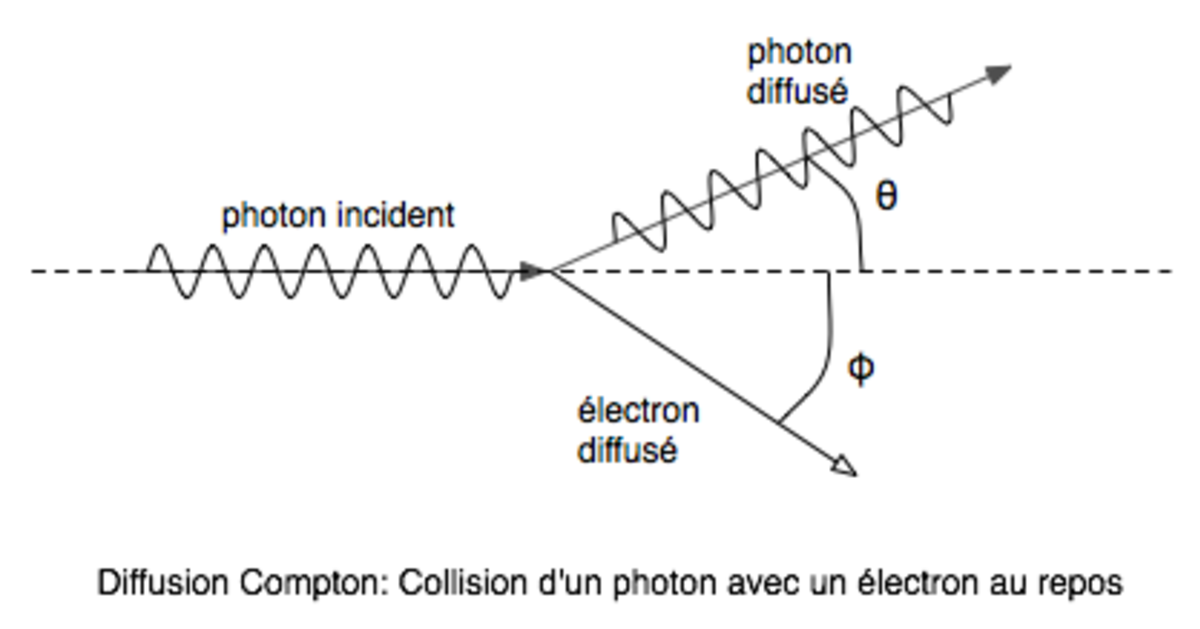
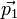
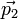
Considérons un photon venant de la gauche et se dirigeant vers la droite avec une impulsion $\vec{p_1}$ et une énergie $E = p 1 c$ . Le photon est diffusé par un électron au repos d'énergie initiale $m e c 2$ . Le photon est diffusé dans une direction faisant un angle $θ$ par rapport à la direction d'origine. 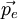L'électron prenant une direction $φ$ , l'impulsion du photon après diffusion sera $\vec{p_2}$ et celle de l'électron $\vec{p_e}$ .

Variation de la longueur d'onde du photon incident

Pour connaître la variation de longueur d'onde du photon dû à la collision, on utilise la conservation de la quantité de mouvement et la conservation de l'énergie. La première s'écrit, selon les directions «x» et «y», respectivement le long de la trajectoire incidente du photon, et sa perpendiculaire (voir la figure):

En isolant le terme contenant $p e$ dans les deux équations, en élevant ensuite au carré, puis en additionnant les deux équations, et finalement en utilisant l'identité trigonométrique: $cos 2 φ + sin 2 φ = 1$ , on obtient:

D'un autre côté, la conservation de l'énergie s'écrit:

où $m e$ et $c$ sont la masse de l'électron, et la vitesse de la lumière respectivement. Le signe $γ$ est utilisé ici comme habituellement pour désigner le photon-lui-même. De nouveau en isolant le terme en ${p_{e}}^{2}$ , on obtient:

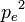
En soustrayant les deux expressions obtenues pour ${p_{e}}^{2}$ , on peut calculer l'expression :

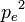
On introduit alors l'hypothèse quantique selon laquelle l'impulsion d'un photon est reliée à sa longueur d'onde $λ$ comme: $p = h / λ$ où $h$ est la constante de Planck. Ainsi, l'équation précédente donne directement la variation de longueur d'onde du photon:

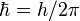
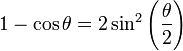
De la même manière, en utilisant $\hbar = h/2\pi$ , et l'identité trigonométrique $1-\cos\theta = 2\sin^2\left(\frac{\theta}{2}\right)$ , on peut écrire:

Cette expression est identique à celle qui s'obtient par un calcul utilisant la mécanique quantique, et les diagrammes de Feynman.

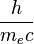
Le facteur : $\frac {h}{m_e c}$ porte le nom de "longueur d'onde de Compton". On le note $λ C$ , il vaut 0,024 Å.

Variation de l'énergie du photon diffusé

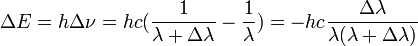
La variation de longueur d'onde va de paire avec une variation d'énergie : $Δ E$ donnée par le Postulat de Planck-Einstein : $\Delta{}E = h \Delta{}\nu{} = hc (\frac {1}{\lambda+\Delta \lambda } - \frac{1}{\lambda} ) = -hc \frac{\Delta\lambda}{\lambda(\lambda+\Delta\lambda)}$ .

Ainsi, si un photon incident possède une énergie : $E 0$ , alors l'énergie de ce photon après diffusion sur un électron de la matière aura l'énergie :

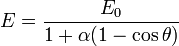
$E = \frac {E_0} {1 + \alpha (1- \cos \theta)}$

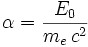
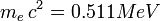
où $\alpha = \frac {E_0}{m_e\,c^2}$ et $m_e\,c^2 = 0.511 MeV$ .

L'énergie perdue par le photon est entièrement distribuée à l'électron sur lequel la diffusion s'est faite, l'électron acquiert ainsi l'énergie cinétique:

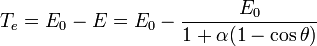
$T_e = E_0 - E = E_0 - \frac {E_0} {1 + \alpha (1- \cos \theta)}$

Nous obtenons ainsi la relation suivante:

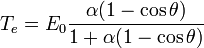
$T_e = E_0 \frac {\alpha (1- \cos \theta)} {1 + \alpha (1- \cos \theta)}$

Distribution angulaire de la diffusion Compton

La diffusion Compton n'est pas isotrope, c'est-à-dire que la probabilité pour un photon d'être diffusé vers un certain angle solide $d Ω$ n'est pas constante: en effet, bien que la probabilité de diffusion vers n'importe quel azimut $χ$ est constante, la probabilité de diffusion vers l'angle polaire $θ$ est plus grande quand $θ$ est proche de 0, c'est-à-dire que le photon a plus de chance d'être diffusé vers l'avant.

La probabilité pour un photon d'énergie $E 0$ d'être diffusé vers un angle $θ$ quelconque est donnée par la formule de Klein-Nishina :

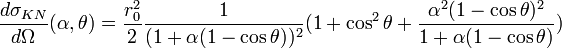
$\frac {d\sigma_{KN}} {d\Omega}(\alpha, \theta) = \frac{r_0^2} {2} \frac {1} {(1 + \alpha (1-\cos{\theta}))^2} (1+ \cos^2{\theta} + \frac {\alpha^2 (1-\cos{\theta})^2} {1 + \alpha (1-\cos{\theta})})$

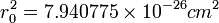
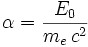
où $r 0$ est le rayon classique d'un électron ( $r_0^2 = 7.940775 \times 10^{-26} cm^2$ ), et $\alpha = \frac {E_0}{m_e\,c^2}$ .

Cette formule montre que la diffusion est symétrique à faible énergie.

Une autre forme plus facile à retenir de cette formule fait intervenir le rapport des énergies du photon avant et après collision :

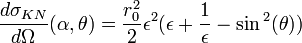
$\frac {d\sigma_{KN}} {d\Omega}(\alpha, \theta) = \frac {r_0^2} {2} \epsilon^2 (\epsilon + \frac {1} {\epsilon} -\sin{}^2(\theta))$

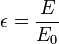
où $\epsilon = \frac{E}{E_0}$

Ainsi la probabilité pour un photon d'énergie $E 0$ de subir une diffusion Compton s'écrit :

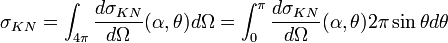
$\sigma_{KN} = \int_{4\pi} {\frac {d\sigma_{KN}} {d\Omega}(\alpha, \theta) d\Omega} = \int^{\pi}_{0} {\frac {d\sigma_{KN}} {d\Omega}(\alpha, \theta) 2\pi \sin{\theta} d\theta}$

Ce qui s'intègre en :

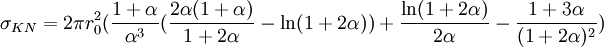
$\sigma_{KN} = 2 \pi r_0^2 ( \frac {1+\alpha} {\alpha^3} (\frac {2 \alpha (1+\alpha)} {1+2\alpha} - \ln(1+2\alpha)) + \frac {\ln(1+2\alpha)} {2\alpha} - \frac {1+3\alpha} {(1+2\alpha)^2} )$

À partir de la formule de Klein-Nishina, il est aussi possible de calculer la probabilité qu'un photon diffusé le soit entre deux angles : $θ1$ et $θ2$ . Calculons pour cela la probabilité de diffusion entre les angles polaires 0 et $θ$ :

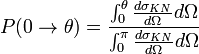
$P(0\rightarrow\theta) = \frac {\int^{\theta}_{0}{\frac {d\sigma_{KN}} {d\Omega} d\Omega}} {\int^{\pi}_{0}{\frac {d\sigma_{KN}} {d\Omega} d\Omega}}$

Ce qui s'intègre en :

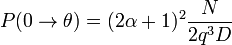
$P(0\rightarrow\theta) = (2\alpha +1)^2 \frac {N} {2q^3D}$

avec:

$q = 1 + α(1 - cosθ)$
$N = 2 q 4 + α q 3 (α + 4) + 2 q 3 (α 2 - 2α - 2) l n q - 2 q 2 (2α + 1) - q α 2$
$D = 4α(α + 1) 2 (2α + 1) + (2α + 1) 2 (α 2 - 2α - 2) l n (2α + 1) - 2α 3 (3α + 1)$

La probabilité $P(\theta1\rightarrow\theta2)$ de diffusion entre les angles $θ1$ et $θ2$ , tels que $θ2 > θ1$ s'écrit alors :

$P(\theta1\rightarrow\theta2) = P(0\rightarrow\theta2) - P(0\rightarrow\theta1)$

Détection des photons diffusés

Diffusion Compton inverse

- Introduction - Histoire de la découverte de l'effet Compton - Détection des photons diffusés - Démonstration - Diffusion Compton inverse

L'origine énigmatique des rayons cosmiques les plus énergétiques ⚡

Le diagnostic de l'autisme remis en cause par l'intelligence artificielle 🩺

Imprimer en 3D avec la lumière du soleil ☀️

La pollution atmosphérique nuit gravement au cerveau 🧠

Le trou noir supermassif Ansky vient de se réveiller ⚫

Voici ce qui rend notre cerveau vraiment unique 🧠

Asymétrie matière-antimatière: une nouvelle pièce du puzzle dévoilée 🧩

Neige en inuit, goût en japonais... comment les langues décomposent la réalité ? 💬

La physique révèle les secrets d'un strike parfait au bowling 🎳

Le TDAH associé à la démence 🧠

Découverte d'une nouvelle forme d'intrication quantique, une première en 20 ans ⚛️

Le régime cétogène montre des surprises sur le cholestérol 🧐

Un tango observationnel révèle une Super-Terre 🔭

Cette expérience montre que la graisse brune augmente fortement la longévité 🕒

L'Univers comme jamais vu auparavant: les révélations du fond diffus cosmologique 🔭

C'est sérieux: de la bave pourrait révolutionner la conception de bioplastiques 🪱

Découverte: le trou noir central de notre galaxie pourrait anéantir la vie sur Terre 💥

Etude scientifique: ces aliments nous font vieillir 🍽️

Pourquoi notre visage est-il plus petit et délicat que celui des Néandertaliens ? 🤔

A 18 ans, il découvre 1,5 million d'objets célestes inconnus avec son algorithme d'IA 🌟

Que sont ces objets rouges et aplatis, qualifiés d'UFOs par les astronomes ? 🔭

Une méthode simple pour améliorer les performances en mathématiques 🧮

Que sont ces étranges éclairs rouges photographiés au-dessus de l'Himalaya ? ⚡

Nous descendons non pas d'un, mais d'au moins deux groupes anciens 🧬

Un nuage géant de 160 000 soleils découvert dans notre Voie lactée 🔭

Connaissez-vous le rat-kangourou musqué, ce marsupial à la démarche unique ? 🦘

Comment une poignée de traders a fait s'effondrer deux cryptomonnaies 📉

Première cartographie titanesque d'un cerveau, avec 500 millions de connexions neuronales 🧠

Cette double supernovae proche est inexorable, voici la date... qui va vous surprendre 💥

Un océan phosphorescent: comment s'explique ce phénomène rare et féerique ? 🌊

L'ELT pourrait-il découvrir une vie extraterrestre dès 2028 ? 🔭

Cet édulcorant tue les superbactéries résistantes 🍬

Les neutrinos, la clé de la gravité quantique ? 👀

En Italie, les éruptions explosives de ce volcan déjouent les pronostics 🌋

Que sont ces spaghettis au cœur de notre galaxie ? 🔭

Des scientifiques ont créé une "bombe intelligente" contre le cancer 🎯

Les nanoplastiques, l'amiante du 21ème siècle ? 🔬

Compétition cellulaire: des forces sculptent nos tissus 🛠️

Le climat en Europe et au États-Unis pourrait changer bien plus radicalement que supposé 🌍

Découverte: ce dinosaure avait des poches d'air dans les os 🦴

La vie sur Titan, si elle existe, ressemblerait à quoi ? 🪐

Magnétisme et biologie s'allient contre le cancer 🧲

WR 104: on en sait plus sur cette "étoile de la mort" qui menace la Terre ☄️

Découverte: des bactéries respiraient de l'oxygène 1 milliard d'années avant la Grande Oxydation 🫧

Découverte d'un nouveau type de vent solaire rapide ☀️

Les dinosaures n'étaient pas en déclin avant l'astéroïde 🦖

Ce robot-cheval est véritablement tout-terrain 🐎

Comment un mauvais sommeil peut endommager votre cerveau ? 🧠

Découverte de microbes cachés qui purifient l'eau sans que nous le sachions 💧

Bonne nouvelle pour les enfants de la Lune 🌙

Page générée en 0.120 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise