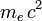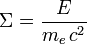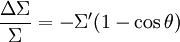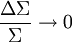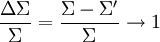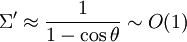Diffusion Compton - Définition
La liste des auteurs de cet article est disponible ici.
Détection des photons diffusés
Supposons qu'un flux Φ de photons d'énergie E0 frappe un petit échantillon de matière contenant Ne électrons. Supposons maintenant que l'on veuille détecter les photons diffusés sur les électrons de cet échantillon à l'aide d'un détecteur sphérique parfait dont l'angle solide apparent, vu de la source est ΔΩdet
Le nombre de photons par seconde détecté par le détecteur est :
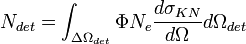
Si de plus le détecteur est assez éloigné de l'échantillon de matière (c'est-à-dire πa2 < < R2, où a est le rayon du détecteur et R sa distance à l'échantillon), on peut considérer que le détecteur se trouve à l'angle polaire θ et que 
.
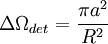
Il détectera alors le nombre de photons par seconde suivant :
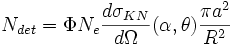
et tous les photons détectés auront une énergie égale à (ou très proche de) :
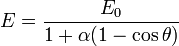
Relation entre l'angle θ de diffusion du photon et l'angle φ d'éjection de l'électron
Supposons que, dans le référentiel du laboratoire, le photon soit diffusé vers un angle θ, alors l'angle d'éjection de l'électron, φ, est donné par la relation suivante :
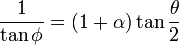
Ainsi si :
- θ = π, alors φ = 0. Cela est facile à comprendre par analogie avec le billard : lorsque la boule blanche (photon) tape directement dans une autre boule (électron) de façon à ce que la blanche revienne en arrière (θ = π), alors l'autre boule va généralement vers l'avant (φ = 0)
- θ = 0, alors
. Ce cas est plus difficile à comprendre mais peut aussi être expliqué par une analogie avec le billard. Lorsque qu'on fait taper la boule blanche (photon) dans une autre boule (électron) de façon à ce que la blanche ne change presque pas de direction et continue tout droit (θ = 0), alors la boule blanche n'a fait qu'effleurer l'autre boule qui est déplacée perpendiculairement à la trajectoire de la blanche ()
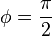
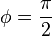
Régimes Thomson et Klein-Nishina
Selon que le photon incident a une très grande énergie ou pas, on distingue deux «régimes» de la diffusion Compton: les régimes dits «Thomson» (qui donne la diffusion Thomson) et «Klein-Nishina». Par commodité, définissons l'énergie en unités naturelles, c'est-à-dire en unités de l'énergie au repos de l'électron :
où me et c sont la masse de l'électron et la vitesse de la lumière, et le dénominateur n'est rien d'autre que le fameux E=mc2. On peut donc réécrire la variation de longueur d'onde ci-dessus en variation d'énergie comme suit :
Pour des photons avec une très faible énergie, c'est-à-dire avec une énergie bien plus faible que l'énergie au repos de l'électron (511 keV), on a évidemment Σ < < 1, et donc :
Ce qui signifie que si le photon a une très faible énergie face à l'électron au repos, sa longueur d'onde ne changera quasiment pas. Seule sa direction va changer. C'est ce qu'on appelle le régime Thomson. Dans ce cas, la diffusion Compton retombe sur le cas particulier de la diffusion Thomson.
Dans le cas contraire où le photon a une grande énergie face à l'électron au repos, Σ > > 1, on obtient alors :
et donc :
où le terme O(1) signifie «de l'ordre de 1». Dans ce cas, le photon incident a une très grande énergie, mais après la collision, il n'a essentiellement que l'énergie d'un électron au repos (
). Il a donc perdu une grande partie de son énergie. On parle alors de perte «catastrophique», et ce régime est appelé «régime de Klein-Nishina». Remarque : l'effet Compton n'est bien sûr pas limité au couple photon-électron. Toute particule chargée électriquement est susceptible d'y être soumise ; cependant, l'effet est plus spectaculaire pour l'électron, la variation de longueur d'onde étant inversement proportionnelle à la masse de la particule (l'électron est la plus légère des particules chargées de l'Univers « ordinaire »).