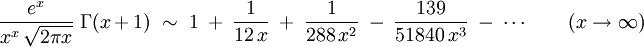Développement asymptotique - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Développement asymptotique
Définition
Supposons que la fonction f ait c1 g1 pour partie principale. On peut alors tenter de mieux préciser le comportement de f en cherchant si la différence f - c1 g1 n'aurait pas à son tour une partie principale c2 g2. Dans l'affirmative, on écrira :
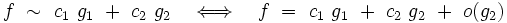
On peut parfois poursuivre ainsi le développement. On appelle alors développement asymptotique à n termes (ou à l'ordre n) de la fonction f par rapport à E l'expression :
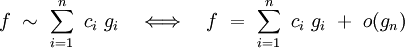
Si un tel développement existe, il est unique. Le terme o(gn) est appelé le reste du développement.
Exemples
- Les exemples les plus simples de développement asymptotiques sont les développements de Taylor (les développements limités à l'ordre n) d'une fonction f(x) qui est n fois dérivable en x0 :

- Mais une fonction peut très bien posséder un développement asymptotique dans un voisinage où il n'existe pas de développement de Taylor (ni même de DL); par exemple, la fonction f(x) ci-dessous admet le développement asymptotique suivant au voisinage de zéro :
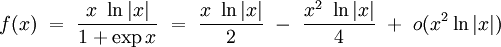
- alors qu'elle n'admet pas de développement limité (à un ordre
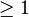
- L'existence d'un développement asymptotique à un nombre arbitrairement grand de termes est un cas très particulier. Par exemple, la fonction f(x) ci-dessous ne possède un développement asymptotique au voisinage de l'infini qu'à un seul terme :
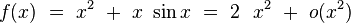
- Parfois même, l'obtention du premier terme du développement est très difficile. Par exemple, soit π(x) le nombre de nombres premiers p inférieurs ou égaux à x. Gauss avait conjecturé qu'au voisinage de l'infini :
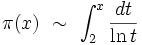
- Il a fallu un siècle avant qu'une démonstration ne soit produite en 1896 par Hadamard et de la Vallée-Poussin !
- La fonction gamma d'Euler admet le développement asymptotique suivant au voisinage de l'infini :