Détermination des constantes d'équilibre - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Les constantes d'équilibre sont évaluées pour quantifier les équilibres chimiques à partir de mesures de concentrations, directes ou indirectes, et mettant en œuvre des techniques numériques.
Cet article se limite aux équilibres en solutions entre solutés pour lesquels l'activité chimique est mesurée par la concentration molaire en mol L-1. Destiné aux praticiens spécialisés ainsi qu'aux apprentis ayant une appréciation de base des équilibres chimiques, cet article traite du sujet en profondeur jusqu'à permettre la programmation des techniques de détermination en se souciant de la rigueur statistique, et s'attarde à l'interprétation objective des résultats.
Introduction
Un équilibre chimique peut s'écrire en général
où l'on distingue les réactifs A, B,..., à gauche de la double flèche, des produits P, Q,... à sa droite. On peut s'approcher de l'équilibre des deux directions, et cette distinction entre réactifs et produits n'est que conventionnelle. La double flèche indique un échange dynamique, plus ou moins rapide, entre réactifs et produits, et l'équilibre est atteint lorsque les concentrations des espèces participantes deviennent constantes. Le rapport des produits des concentrations, habituellement représenté par K et appelé la constante d'équilibre, s'écrit conventionnellement avec les réactifs au dénominateur et produits au numérateur ainsi
-
![K = \frac {[P]^p[Q]^q...}{[A]^a[B]^b...}](https://static.techno-science.net/illustration/Definitions/autres/9/91ec2ac7e5a263db661a81cf2d078bfa_511d101be6e64d66cc463cb2047597b1.png)
Ce rapport sera alors constant à une température donnée, pourvu que le quotient des activités chimiques est constant, supposition qui sera valide à une force ionique élevée, faute de quoi ce seront les activités qu'il faudra évaluer. Il exprime la position de l'équilibre, plus ou moins favorable (K > 1) ou défavorable (K < 1), que l'on peut quantifier si l'on peut mesurer la concentration de l'une des espèces en équilibre, avec l'aide des quantités analytiques (concentrations, masses ou volumes) des réactifs mis en œuvre.
Plusieurs types de mesures sont possibles. Cet article touche les trois types principalement utilisés et leurs limitations. Plusieurs autres, plus rares, sont décrits dans l'œuvre classique de Rossotti et Rossotti.
Sauf s'il s'agit d'un système expérimental très simple, les rapports entre les constantes d'équilibre et les concentrations mesurées seront non-linéaires. Avec un ordinateur rapide et un logiciel équipé, et ayant une quantité suffisante de mesures de concentration, la détermination d'un nombre indéfini de K, impliquant un nombre indéfini d'espèces en solution, se fait facilement et de manière statistiquement rigoureuse par solution numérique des rapports non-linéaires qui décrivent un système d'équilibres enchevêtrés. Cette détermination suit alors le parcours d'une modélisation, avec trois étapes: l'articulation d'un modèle, sa numérisation et son affinement. Cet article détaille ces trois étapes et finit par proposer certains logiciels utiles.
Méthodes de calcul
Les données de base incluront pour chaque échantillon les concentrations analytiques des réactifs mis ensemble pour constituer les espèces complexes en équilibre entre eux et avec les réactifs libres, ainsi qu'une mesure de la concentration d'une espèce ou de plusieurs espèces. Le nombre de mesures sera préférablement supérieur (et au minimum égal) au nombre de valeurs inconnues (constantes d'équilibre en cause, ainsi que les valeurs d'ε ou de δ à déterminer). Moins on aura d'inconnues à déterminer à la fois, plus chaque détermination sera fiable.
Linéarisations dangereuses
Une détermination graphique est parfois possible avec un système expérimental simple impliquant un ou deux équilibres. Cela nécessite une linéarisation avec ou sans approximations des rapports non-linéaires entre constantes d'équilibre et les concentrations mesurées, d'où l'on soutirera la valeur du ou des K avec la pente ou l'intercepte ou avec une combinaison des deux. Il va sans dire que toute approximation amoindrira la généralité de la détermination. Même si l'on peut obtenir les valeurs exactes de la pente et de l'intercepte par calcul (méthode des moindres carrés) plutôt que par estimation visuelle, ce genre de détermination peut violer un principe de base en statistique des modèles linéaires, soit que la distribution des erreurs de mesure (erreurs affligeant les y dans un rapport linéaire y = mx + b) sera aléatoire et à distribution normale des amplitudes. Bien que l'on puisse s'attendre à ce que les erreurs de mesure obéiront une distribution normale, ce ne sera pas le cas des fonctions de ces mesures qui résulteront d'une linéarisation des équations régissant les équilibres en cours.
En guise d'exemple, l'équation de Henderson-Hasselbalch est une linéarisation courante pour quantifier un équilibre simple. Elle peut être utilisée de manière statistiquement rigoureuse ou dangereuse. Dans le cas d'une titration d'acide faible HA avec une solution d'hydroxyde, on propose le modèle
où un volume vi de solution d'hydroxyde à teneur [OH − ]0 est livrée à une solution d'acide à teneur initiale [HA]0 pour ensuite mesurer le pHi résultant. Cette équation a la forme
Puisqu'ici on oppose la mesure elle-même (le pHi) aux paramètres connus (les constantes [HA]0 et [OH − ]0 et la variable vi), la détermination du pKa sera rigoureuse, pourvu que l'on ne calcule pas de pente chimérique (voir plus bas).
Par contre, un cas contraire fait partie des travaux pratiques d'un cours de chimie d'une université américaine. Il s'agit d'une détermination spectrométrique du pKa d'un indicateur I,
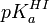
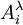
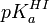
Mais le pH n'est pas contrôlé directement; plutôt, on le calcule avec la seconde application de l'équation de Henderson-Hasselbalch, tout en connaissant le pKa d'un tampon HA,
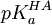
On y reconnaîtra la forme
analogue à celle du premier exemple.
Le fait qu'il y ait double application de l'équation de Henderson-Hasselbalch n'est pas problématique. Le problème est que ce n'est pas la mesure Aλ qui est opposée aux paramètres connus, mais bien une fonction non-linéaire de la mesure, plus précisément une différence de fonctions logarithmiques,
-
![y=\log_{10} \lbrace A_i^{\lambda}-\epsilon_{HI^+}^{\lambda}\ell[I]_0 \rbrace-\log_{10} \lbrace \epsilon_{I}^{\lambda}\ell[I]_0-A_i^{\lambda} \rbrace](https://static.techno-science.net/illustration/Definitions/autres/d/d2fbc8fc3852384528498076c9185ba3_0f5fd7d4b4dd5c6b48ba21e1fa463876.png)
Bien que l'on peut espérer une distribution aléatoire des erreurs de mesure Aλ et que l'amplitude de ces erreurs obéira une distribution normale, ce ne sera certainement pas le cas chez la quantité complexe y même si les ε et le [I]0 sont sans erreur possible, ce qui n'est pas le cas. Au contraire, cette détermination imposera une distribution aléatoire des résidus
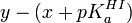
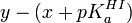
Un autre problème survient avec ces deux exemples : un expérimentaliste mal avisé verra dans la relation y = x + pKa un modèle linéaire de forme générale y = mx + b et aura le réflexe de calculer une pente et un intercepte par la méthode des moindres carrés, souvent à l'aide d'une fonction préconstruite d'un logiciel (par exemple Excel de Microsoft). alors qu' il n'y a pas de pente à déterminer. Non seulement la valeur du pKa ainsi calculé ne sera pas justifiable, les statistiques de confiance dans le résultat, basées sur une détermination de deux inconnues, seront alors faussées. Le pKa n'est pas en fait un intercepte à déterminer en extrapolant vers x = 0, mais la simple moyenne des différences y − x, et la confiance en la valeur du pKa ainsi obtenue sera donnée par la déviation standard autour de cette moyenne. La tentation de déterminer un pente chimérique est d'autant plus grande que la déviation standard du pKa calculé avec une pente sera plus petite, puisque la modélisation d'une relation à l'aide de deux paramètres (pente et intercepte) sera toujours plus satisfaisante qu'à l'aide d'un seul paramètre (l'intercepte, dans le cas présent).
Modélisation non-linéaire
Quand un système met en œuvre plusieurs équilibres ou quand les équilibres mettent en cause plusieurs espèces chimiques à la fois, une linéarisation devient impossible sans y imposer des restrictions (approximations). Même si l'on se conforme aux exigences d'un modèle linéaire, toute restriction rend la détermination approximative et moins générale. C'est alors qu'un traitement numérique s'impose.
Dans l'exemple ci-haut, où la linéarisation ne donnait pas un modèle linéaire valide, on aurait dû s'en tenir à une relation f non-linéaire
En général, on travaille avec une relation
-
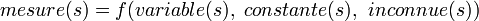
On ne peut pas trouver les inconnues par solution directe. De toute façon, l'équation ne sera pas exacte, étant donné qu'il y aura des erreurs de mesure, des erreurs dans les variables, des erreurs systématiques dans les constantes et la possibilité que les paramètres inconnus ne suffiront pas ou ne seront pas les plus justes. Plutôt, on écrit
- mesure(s) = calcul(s) + erreur.
où les calcul(s) sont obtenus avec
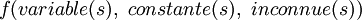
Le problème de la minimisation des résidus n'est qu'un problème technique et il existe plusieurs algorithmes qui se vantent certains avantages. Tous doivent arriver à la même conclusion sur un même modèle décrivant un même système. Cet article cherche moins à comparer les diverses méthodes numériques qu'à assurer une approche statistiquement valide, approche qui pourra alimenter une programmation des calculs.
La méthode décrite ici suit le cheminement de Alcock et al. (1978) pour un régime général d'équilibres multiples.
Le modèle chimique
Le modèle chimique doit inclure toutes les espèces en équilibre de sorte à permettre un calcul de chacune de leur concentration, impliquant autant d'équilibres qu'il y a d'espèces en solution. Il y a deux genres de constantes d'équilibre utilisés pour ce faire: les constantes générales et les constantes de formation cumulative.
Une constante dite générale gouverne un équilibre entre n'importe quelles espèces, par exemple un équilibre d'échange de ligands entre deux complexes de coordination, par exemple
-
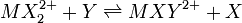
![K = [MXY^{2+}][X]/[MX_2^{2+}][Y]](https://static.techno-science.net/illustration/Definitions/autres/f/f8c305c4e75709f3e222db6e051cf41c_48e90a808056ec13c1506a3198ad5724.png)
Une constante de formation cumulative se limite à un équilibre entre une espèce et les réactifs irréductibles qui la forment par cumul. Comme tout ensemble en équilibre survient après avoir mélangé des réactifs, on définit donc toute espèce comme le résultat ApBq... d'une combinaison stoichiométrique et unique des réactifs irréductibles A, B, ...
spécifiée par les coefficients de stœchiométrie p, q, ..., et la constante d'équilibre qui régit cette formation est habituellement symbolisé par un β, ainsi
Ce faisant, nous garantissons autant de constantes que d'espèces et aucun équilibre ne sera redondant. Même les réactifs irréductibles peuvent être représentés de la même manière, avec des β symboliques,
-
![[A]^{ _{ }} = \beta_{10...}[A]^1[B]^0...](https://static.techno-science.net/illustration/Definitions/autres/a/a03b831a12836bea2c8f89fcb1e6819d_c4a98285567b00652966db92d5e960fe.png)
![\beta_{10...^{}} ={[A_1B_0...]}/{[A]^1[B]^0...}=1](https://static.techno-science.net/illustration/Definitions/autres/3/3d5a7390dad2c80b28c3a63554ff987c_b225f01bc321f6df2ff82878d83902bd.png)
-
![[B]^{ _{ }} = \beta_{01...}[A]^0[B]^1...](https://static.techno-science.net/illustration/Definitions/autres/8/840da526829a995334bfbad65d128230_282916943334fd5d12d4676abb2c177c.png)
![\beta_{01...^{}} ={[A_0B_1...]}/{[A]^0[B]^1...}=1](https://static.techno-science.net/illustration/Definitions/autres/a/a0f07c670b545899915b36750ec97145_3b3b0dcd2636fafa60706b790f17756c.png)
-

pour que toutes les espèces soient traitées de façon homogène. De façon générale, la concentration de la i ième espèce Ei, formée d'une combinaison de NR réactifs R, est
où le coefficient de stœchiométrie ai,k est le nombre d'équivalents du k ième réactif entrant dans la formation de la i ième espèce, et où βi est la constante d'équilibre qui régit cet assemblage. Cette représentation harmonisée facilitera la notation à venir et la programmation des logiciels.
Il s'avère que cette deuxième sorte d'équilibre est d'utilité tout aussi générale que la première. En effet, tout ensemble d'espèces en équilibres multiples pourra être modelé à l'aide d'équilibres de formation (bien qu'ils ne seront pas toujours le meilleur choix) et, une fois le système d'équations résout et les β déterminés, tout autre équilibre ne sera qu'une combinaison de ces mêmes équilibres de formation, et toute autre constante ne sera qu'une combinaison de ces mêmes β et pourra donc être quantifié par la suite (voir ). Pour reprendre l'exemple d'échange de ligands entre complexes de coordination cité ci-haut, nous pouvons écrire
-
![K = [MXY^{2+}][X]/[MX_2^{2+}][Y] = \beta_{111} \beta_{010}/\beta_{120} \beta_{001}](https://static.techno-science.net/illustration/Definitions/autres/5/523da32fcddb2a7352f94ac146e0db8a_816668280235cc548d49f2964bc06e84.png)
- où
![\beta_{111} = \frac{[MXY^{2+}]}{[M^{2+}][X][Y]}](https://static.techno-science.net/illustration/Definitions/autres/e/e9df1dbea9debbc44c4e3612ed6a9144_fe7e8357a5c4d73ec517c63a3efa031a.png)
![\beta_{120} = \frac{[MX_2^{2+}]}{[M^{2+}][X]^2[Y]^0}](https://static.techno-science.net/illustration/Definitions/autres/e/ec946c6f6054f1438723f18c8e029115_25c77e7e0aac72fe93712c7bb1198c5f.png)
![\beta_{010} = \frac{[X]}{[M^{2+}]^0[X][Y]^0}(=1)](https://static.techno-science.net/illustration/Definitions/autres/a/aa0920f5a0162daf2f6ebbdce919b3d4_bc12af9705bd0091b2a90058d908f907.png)
![\beta_{001} = \frac{[Y]}{[M^{2+}]^0[X]^0[Y]} (=1)](https://static.techno-science.net/illustration/Definitions/autres/7/76e5856a377a36696bebdd2f3c188da5_37d05cdbb0365a4b0f44459961a399d1.png)
Le grand avantage d'une telle formulation à l'aide d'équilibres de formation est que le calcul des concentrations (section suivante) est grandement simplifié.
Dans tous les cas, si l'expérience est conduite en milieu aqueux, il faudra inclure la dissociation de l'eau (son autoprotolyse)
et imposer la valeur du produit ionique KW appropriée à la situation en tant que constante connue. Si H + or OH − est un des réactifs, disons A, la dissociation de l'eau peut être représentée en utilisant la même notation que celle des équilibres de formation, par
-
![\beta_{-10...^{ }}= K_w = {[OH^-]}/{[H^+]^{-1}[B]^0...}](https://static.techno-science.net/illustration/Definitions/autres/f/fe0fa4df62e79682a9e2025f08e2d24b_62bb1d2222c59d75ade7f6e7e652c70c.png)
![{[H^+]}/{[OH^-]^{-1_{ }}[B]^0...}](https://static.techno-science.net/illustration/Definitions/autres/c/c634aada6e226e0df6a1a6111386b7aa_cdfb4d03402acc4209ccf9ec0952acb9.png)
Si jamais la valeur du KW n'était pas connu pour la situation expérimentale voulue, par exemple dans un mélange de solvants particulier et(ou) à une température particulière, on pourrait la considérer comme quantité inconnue à déterminer en même temps que les autres constantes inconnues, mais il serait plus sage de la déterminer auparavant, indépendamment, par exemple par la méthode de Gran, pour limiter le nombre d'inconnus à traiter par expérience et la corrélation entre les résultats.
Il va sans dire que le modèle doit être complet, dans le sens que doivent y paraître tous les équilibres enchevêtrés qui risquent d'agir sur la mesure. Toutefois, il est usuel d'omettre du modèle les espèces que l'on anticipe n'exister qu'en concentrations négligeables, par exemple les équilibres mettant en cause l'électrolyte que l'on ajoutera pour maintenir une force ionique constante ou les espèces-tampons qui maintiendront un pH constant. Après avoir numérisé les équilibres et jugé du succès de la modélisation, on aura l'occasion de revoir la pertinence des espèces incluses et la nécessité d'y inclure des espèces non-anticipées.
Numérisation
À un ensemble de β correspondra un ensemble unique de concentrations, parce qu'elles sont bornées par les quantités des matériaux utilisées.
La quantité de chaque réactif mis en réaction, maintenant dispersée parmi toutes les espèces complexes qu'il forme ainsi qu'en forme libre, restera constante dans un échantillon donné, et sera donc connue dans chaque échantillon (ou à chaque étape d'une titration) selon les volumes et les concentrations des stocks mélangés pour préparer l'échantillon. Pour chaque réactif R, on aura donc une concentration analytique connue [R]connue dans chaque échantillon. On cherchera alors les concentrations de toutes les espèces formées par ce réactif, ainsi que le reste inutilisé du réactif (réactif libre), de sorte que le total de leurs parts en R, [R]calc, soit égal à [R]connue. La somme des parts du j ième de NR réactifs formant les NE espèces E, s'écrit
où le coefficient stœchiométrique ai,j indique le nombre d'équivalents du j ième réactif contenu dans l'i ième espèce. Ainsi, l'unicité des valeurs des concentrations pour chaque ensemble de β est assuré par les NR [R]connue correspondant aux NR 'inconnus' [Rk].
La détermination trouvera donc l'unique ensemble des β qui fixeront les concentrations des espèces qui reproduiront le mieux les mesures expérimentales et il suffira d'avoir au moins autant de mesures que de β inconnus.
La stratégie à suivre consiste donc à
- calculer les concentrations estimées des NE espèces E en calculant les concentrations estimées des NR réactifs libres R à partir d'estimations des valeurs des β inconnus, ce qui requiert que les [R]calc et les [R]connue soient mis en accord par ajustement des [Rk] de manière itérative
- comparer la mesure à ce que les concentrations ainsi estimées permettent d'anticiper, c'est-à-dire comparer la mesure réelle à celle estimée, selon le rapport entre la quantité mesurée et les concentrations dont la mesure dépend
- calculer et appliquer un ajustement aux valeurs des β inconnus
- recalculer les concentrations des réactifs libres
- re-comparer les mesures réelles et estimées
- ré-ajuster les β inconnus
- et ainsi de suite de manière itérative, jusqu'à ce que l'accord des mesures réelles et estimées ne puisse plus être amélioré, nous permettant de conclure que les β auront donc été déterminés.
Calcul des concentrations
À chaque itération de la détermination, les concentrations doivent être calculées, mais il n'est pas possible de résoudre directement les NR équations parallèles
- [Rj]connue = [Rj]calc
parce qu'elles ne sont pas linéaires. Plutôt, la méthode Gauss-Newton est adoptée, où l'on se rapprochera petit à petit de la solution à partir d'un début approximatif où auront été estimées les concentrations [R]. À la μ ième itération, on calculera des corrections Δ[Rk]μ à apporter aux valeurs en cours [Rk]μ pour générer de meilleures estimations des [Rj]calc et qui serviront à la (μ + 1) ième itération. Ces corrections proviendront de la solution des séries de Taylor (tronquées pour ne retenir que les termes de premier ordre)
que l'on peut rassembler en notation matricielle-vectorielle ainsi
où le (j,k) ième élément de la matrice
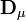
![{\partial [R_j]_{\mu}^{calc}}/{\partial [R_k]}](https://static.techno-science.net/illustration/Definitions/autres/3/349f4e2f69b383b7bfb23145a0334047_4fc6bc8b2445d27cd3cbc0f956191a83.png)
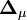
puisque la matrice
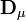
Affinement des constantes d'équilibre
L'affinement des valeurs des constantes d'équilibre inconnues se fait d'habitude en minimisant, par la méthode des moindres carrés non-linéaire, une quantité U (aussi dénoté par χ2) appelée fonction objectif:
où les y représentent les mesures et les ycalc sont les quantités que les concentrations des espèces permettent d'anticiper. La matrice des pondérations,
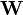
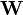
où Wi,j = 0 quand
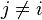
Les éléments sur la diagonale Wi,i peuvent être estimés par la propagation des erreurs avec
pour tous les paramètres Q (les variables et constantes connues) qui ne seront pas déterminés mais qui constituent des sources d'erreurs expérimentales, où σ(Qj) est une estimation réaliste de l'incertitude sur la valeur du j ième paramètre Q. Ceci reconnaît que chaque paramètre n'aura pas nécessairement une influence uniforme sur tous les échantillons, et la contribution de chaque résidu (y − ycalc) sera désaccentuée selon son incertitude cumulée de toutes les sources d'erreur.
On peut en principe trouver le U minimum en mettant à zéro les dérivées de U par rapport à chaque paramètre inconnu P, mais on ne peut pas en retirer les valeurs des P directement. Plutôt, tout comme pendant le (section précédente), la méthode Gauss-Newton exprime les mesures sous forme de séries de Taylor tronquées
ou, en forme matricielle-vectorielle,
ou
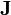
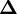
Les corrections ΔP sont calculées avec
où l'exposant T indique la matrice transposée. La matrice
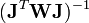
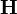
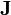
Modification de Levenberg-Marquardt
Aussi appelée méthode ou algorithme de Marquardt-Levenberg.
Dépendant du point de départ, les corrections de Gauss-Newton peuvent être largement excédentaires, dépassant le minimum, ou menant à une augmentation du U (ce qui causerait normalement un affinement avorté) ou même causer des oscillations autour du minimum. Dans d'autres situations, l'approche du minimum peut être lente. Pour amortir les corrections trop grandes ou accélérer l'atteinte du U minimal, on peut faire appel à l'algorithme de Marquardt-Levenberg, couramment utilisée, et appliquer des corrections modifiées
où λ est un paramètre ajustable, et
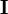
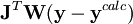
Modification de Potvin
Puisque chaque itération sur les β entraîne un nouveau calcul des concentrations, lui-même itératif, les re-calculs nécessités par la technique de Marquardt-Levenberg lors d'une même itération sont coûteux, surtout s'il y a un grand nombre de données à traiter. Le même problème survient avec d'autres méthodes d'optimisation numérique à paramètre ajustable, telles que les méthodes de Broyden-Fletcher-Goldfarb-Shanno (recherche linéaire du paramètre optimal) ou de Hartley-Wentworth (recherche parabolique).
Ayant noté que ce sont les corrections positives aux valeurs sous-estimées des log10β (ou négatives aux valeurs sur-estimées des β) qui produisent un dépassement du U minimum, tandis que les corrections négatives ne le font pas, et que la taille de ces corrections excessives grandit de façon exponentielle plus on est éloigné du minimum, Potvin (1992a) a proposé une simple modification logarithmique des corrections positives, soit pour la correction Δq du q ième log10β
Cette formulation découle d'une solution approximative des séries de Taylor à ordre infini. Les corrections ainsi modifiées sont de taille beaucoup plus raisonnable, surtout si on est loin du minimum. Bien que ces corrections modifiées puissent quand même dans certains cas mener à un léger dépassement du minimum ou même à une augmentation du U, ce ne sera que temporaire puisque l'itération suivante reviendra dans la bonne direction sans dépassement. L'algorithme limite aussi toute correction négative si la descente du gradient propose au contraire une correction positive. Le grand avantage de cette modification est son coût minime.
Particularités pour données spectrophotométriques
Selon le modèle chimique général exposé plus haut, la loi de Beer-Lambert peut être ré-écrite en termes des concentration des espèces E
qui, en notation matricielle, donne
où la matrice
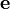
Il y a deux approches généralement adoptées pour le calcul des constantes d'équilibre et des ε inconnus. On peut ré-exprimer les ε en fonctions des absorbances et écrire
-
![\mathbf{A}= \{ (\mathbf{[E]}^T \mathbf{[E]})^{-1} \mathbf{[E]}^T \mathbf{A}\} \mathbf{[E]}](https://static.techno-science.net/illustration/Definitions/autres/6/6e4e03fbe7649060e0301cdd36b5c576_33e252acf9930d3e23ebe41c45eb4d54.png)
ce qui permettra un affinement simultané des constantes d'équilibre et des ε inconnus. L'autre approche, celle utilisée par les auteurs de Hyperquad et de Specfit par exemple, consiste à séparer le calcul des ε de celui des constantes d'équilibre, de n'affiner que les constantes d'équilibre et de calculer les ε avec les concentrations résultantes. Ainsi, en partant d'une série de valeurs estimées des ε, on affine les constantes d'équilibre en optimisant l'accord du modèle avec les mesures d'absorbance à l'aide de la Jacobienne, comme décrit ci-haut, puis les ε sont mis à jour avec
et les nouvelles concentrations [E] qui en résultent. Ensuite, on utilise ces nouvelles estimations des ε pour lancer un nouvel affinement des constantes d'équilibre, ce qui mène à une nouvelle série d'estimations des ε, et ainsi de suite. Ce ping-pong continue jusqu'à ce que les deux familles de paramètres ne changent plus. Les auteurs de Specfit montrent comment trouver les dérivés de la matrice pseudo-inverse
![(\mathbf{[E]}^T \mathbf{[E]})^{-1} \mathbf{[E]}^T](https://static.techno-science.net/illustration/Definitions/autres/b/b510e304fad8803001f2d2ec16c4f098_d658c5e25dd4aee1d4c547823b490cf2.png)
Particularités pour données par RMN
La formulation usuelle, présentée au départ, qui relie la mesure
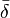
L'utilisation ici de la concentration analytique [Rk]connue, plutôt que la somme des parts appartenant à chaque espèce, [Rk]calc, renforce le fait que le dénominateur commun à toutes les fractions molaires est constant et ne varie pas avec les β. Lors du calcul des concentrations à chaque itération sur les β, les [Rk]calc seront de toute façon ajusté de sorte à égaler les [Rk]connue.
En notation matricielle, on a
où la matrice
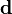
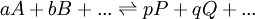
![pH_i = pK_a^{HA}+\log_{10} \frac {[A^-]_i}{[HA]_i} = pK_a^{HA}+\log_{10} \frac {[OH^-]_i}{[HA]_0-[OH^-]_i} = pK_a^{HA}+\log_{10} \frac {v_i[OH^-]_0}{[HA]_0-v_i[OH^-]_0}](https://static.techno-science.net/illustration/Definitions/autres/d/ddb59716dcae281cc790396cce042859_8338f7a80b36239a600c246c5b50d353.png)
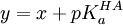
![\log_{10} \frac {[I]_i}{[HI^+]_i} = \log_{10} \frac {A_i^{\lambda}-\epsilon_{HI^+}^{\lambda}\ell[I]_0}{\epsilon_{I}^{\lambda}\ell[I]_0-A_i^{\lambda}} = pH_i + pK_a^{HI}](https://static.techno-science.net/illustration/Definitions/autres/0/0629d01c8590789f0b03e45a180adfd1_ef126d139fae1ff934314068ec65b47f.png)
![\log_{10} \frac {A_i^{\lambda}-\epsilon_{HI^+}^{\lambda}\ell[I]_0}{\epsilon_{I}^{\lambda}\ell[I]_0-A_i^{\lambda}} = pK_a^{HA}+\log_{10} \frac {v_i[OH^-]_0}{[HA]_0-v_i[OH^-]_0}+ pK_a^{HI}](https://static.techno-science.net/illustration/Definitions/autres/c/c19a69dda0e5aa1a67037563c0e326dd_aac9720038f694b4e6a85906f34489eb.png)
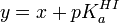
![A_i^{\lambda} = f (v_i, [OH^-]_0, [A]_0, pK_a^{HA}, \epsilon_{I}^{\lambda}, \epsilon_{HI^+}^{\lambda}, \ell, [I]_0, pK_a^I)](https://static.techno-science.net/illustration/Definitions/autres/9/95cad046c843712a1cab08236a8564df_627a0842d3dc5a653321f2231d6feabf.png)
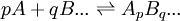
![\beta_{pq...}=\frac{[A_pB_q...]} {[A]^p[B]^q...}](https://static.techno-science.net/illustration/Definitions/autres/3/381e4534957fede5aba2929df1f7ecf8_200d79cdb931e066b63866c9139a3c13.png)
![[E_i] = \beta_i \prod_k^{N_R} [R_k]^{a_{i,k}}](https://static.techno-science.net/illustration/Definitions/autres/f/f96e510fc07e7a9690ff9985ad129f6c_6ddd293b61b8c9ed9bfabe6188750e95.png)
![K_W=[H^+_{ }][OH^-]](https://static.techno-science.net/illustration/Definitions/autres/8/87500672d366e06d4a0aa964bdf0a994_03e5b7193f8e88e704f8aad87b8f14e1.png)
![[R_j]^{calc}= \sum_i^{N_E} a_{i,j} [E_i] = \sum_i^{N_E} a_{i,j} \beta_{i} \prod_k^{N_R} [R_k]^{a_{i,k}}](https://static.techno-science.net/illustration/Definitions/autres/d/da183564d40dedb2c1c7b720ade499d2_a1aabb87409b408f2862b38c6ee60b0b.png)
![[R_j]^{connue} = [R_j]_{\mu}^{calc} + \sum_k^{N_R} \frac {\partial [R_j]_{\mu}^{calc}}{\partial [R_k]} \Delta [R_k]_{\mu}](https://static.techno-science.net/illustration/Definitions/autres/3/3a8918672f409e657cd15ee2267ccaa8_ceced65fecd80ff18ae4491638536f84.png)
![\mathbf{[R]}^{connue} = \mathbf{[R]}_{\mu}^{calc} + \mathbf{D}_{\mu}\, \mathbf{\Delta}_{\mu}](https://static.techno-science.net/illustration/Definitions/autres/8/8dce58b7a7ba09fa8b3c93676d7df4fe_8fadff6d1b501917bb8c0285dcfb301a.png)
![\mathbf{\Delta}_{\mu} = \mathbf{D}_{\mu}^{-1}\ (\mathbf{[R]}^{connue} - \mathbf{[R]}_{\mu}^{calc})](https://static.techno-science.net/illustration/Definitions/autres/d/d40c31ef70568accd464876b3761d8ad_d34ae7e5b3f8c43d1505552da1b245ee.png)
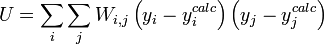
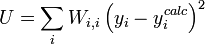
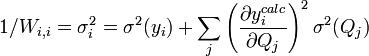
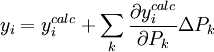
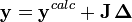
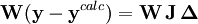
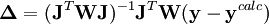
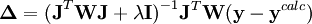
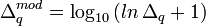
![A^{\lambda}=\ell \sum_i {\epsilon^{\lambda}_i [E_i]}](https://static.techno-science.net/illustration/Definitions/autres/3/37bc164eaa6d9848b0ae6ed4b71701c2_3cf6ca38bbb9981eceeb09ca76ca738f.png)
![\mathbf{A}=\ell \, \mathbf{e} \,\mathbf{[E]}](https://static.techno-science.net/illustration/Definitions/autres/e/ee2afc7e4e8bde9de0b30068e2a79eec_dd572d443ecb9dbac58ae96367a0dc27.png)
![\mathbf{e} = \{(\mathbf{[E]}^T \mathbf{[E]})^{-1} \mathbf{[E]}^T \mathbf{A}\} / \ell](https://static.techno-science.net/illustration/Definitions/autres/d/de3f544869350214ae332cd21110237c_9e231768bbe85534abc1da7718174356.png)
![\bar{\delta} = \frac {1}{[R_k]^{connue}} \sum_i^{N_E} \delta_i a_{i,k} [E_i]](https://static.techno-science.net/illustration/Definitions/autres/2/2c5d516413d020370fdecaeadf983d64_fffb0136f316604f4fb727c0e90efbad.png)
![\mathbf{[R]}^{connue} \mathbf{\bar{\delta}} = \mathbf{a [E] d}](https://static.techno-science.net/illustration/Definitions/autres/5/5f3331ba06db73c93a0b302cfd5138f3_5970aad8fb86b5841fdb3458117b4daf.png)
![\mathbf{d} = [(\mathbf{a [E]})^T (\mathbf{a [E]})]^{-1} (\mathbf{a [E]})^T \mathbf{[R]}^{connue} \mathbf{\bar{\delta}}](https://static.techno-science.net/illustration/Definitions/autres/c/cb39285c066c129ae96daecf8348be37_cbb94a93e9d89ec77b0675c11864573d.png)

















































