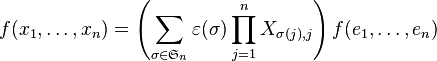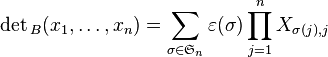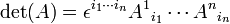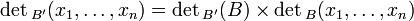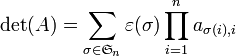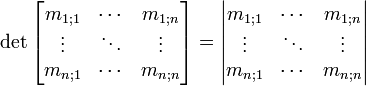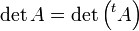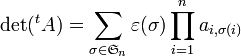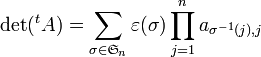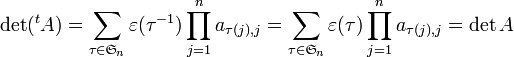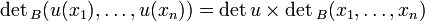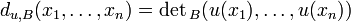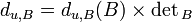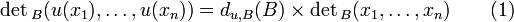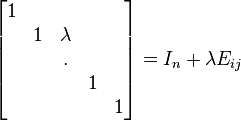Déterminant (mathématiques) - Définition
La liste des auteurs de cet article est disponible ici.
Définition du déterminant
Origine de la construction du déterminant
Les notions de parallélogramme et de parallélépipède sont généralisées à un espace vectoriel E de dimension finie n sur

Il convient de voir dans ce parallélotope une sorte de pavé oblique.
Lorsque l'espace est muni d'un produit scalaire, il est possible de définir le volume de ce parallélotope, parfois appelé son hypervolume pour souligner que la dimension de l'espace concerné n'est pas forcément 3. Il vérifie les propriétés suivantes :
- les volumes de deux pavés adjacents par une face, s'ajoutent
- la multiplication d'un des vecteurs définissant le pavé par une constante induit la multiplication du volume par cette constante
- le volume d'un pavé formé par la répétition du même vecteur (ce qui constitue un cas particulier de pavé plat), est nul.
Un changement de produit scalaire sur l'espace E modifie les mesures de longueurs, angles, et par conséquent de volumes. Cependant la théorie des déterminants montrera qu'à une constante multiplicative près, il n'existe qu'une unique méthode de calcul des volumes dans un espace vectoriel de dimension n.
En reprenant un espace vectoriel sans structure particulière, la notion de déterminant a pour objectif de donner un sens intrinsèque au « volume » du parallélotope, sans référence à un produit scalaire par exemple, c'est-à-dire de construire une fonction f, qui à x1, ..., xn associe un réel, et vérifie les propriétés précédentes. Une telle application est appelée une forme n-linéaire alternée.
Formes n-linéaires alternées
La notion de forme n-linéaire alternée généralise les propriétés précédentes. Elle se définit comme une application de En dans

- linéaire en chaque variable. Ainsi pour des vecteurs x1, ..., xn, x'i et deux scalaires a et b
- alternée, signifie qu'elle s'annule à chaque fois qu'elle est évaluée sur un n-uplet contenant deux vecteurs identiques
L'article application multilinéaire procède à l'étude systématique des formes n-linéaires alternées sur un espace vectoriel de dimension n.
Le résultat principal est la possibilité de ramener le calcul de l'image de (x1,...,xn) à celui d'images des vecteurs de base par n-linéarité. En outre le caractère alterné permet de changer l'ordre des vecteurs, de sorte qu'il suffit de connaître l'image f(e1,...,en) des vecteurs d'une base, pris dans l'ordre, pour connaître f. Remettre les vecteurs dans l'ordre fait intervenir la notion de permutation.
Théorème
L'ensemble An(E) des formes n-linéaires alternées sur un espace vectoriel de dimension n constitue un espace vectoriel de dimension 1.
De plus, si
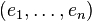
avec Xij la i-ème composante de xj et
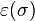
Déterminant d'une famille de n vecteurs dans une base
Définition
On suppose E muni d'une base
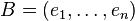
Il faut se représenter cette quantité comme une sorte de volume de pavé, relativement à la base B.
Formule de Leibniz
Soient x1,...xn des vecteurs de E. Il est possible de représenter ces n vecteurs par n matrices colonnes, formant par juxtaposition une matrice carrée X.
Le déterminant de x1,...xn relativement à la base B vaut alors
Cette formule porte parfois le nom de Leibniz. Elle présente peu d'intérêt pour le calcul pratique des déterminants, mais permet d'établir plusieurs résultats théoriques.
En physique, on rencontre souvent la formule de Leibniz exprimée à l'aide du symbole de Levi-Civita, en utilisant la convention d'Einstein pour la sommation des indices :
Formule de changement de base
Si B et B ’ sont deux bases de E, les applications déterminants correspondantes sont proportionnelles (avec un rapport non nul)
Ce résultat est conforme à l'interprétation en termes de volume relatif.
Déterminant d'une matrice
Soit une matrice A=(aij) carrée d’ordre n à coefficients réels. Les vecteurs colonnes de la matrice peuvent être identifiés à des éléments de l'espace vectoriel
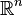
Il est alors possible de définir le déterminant de la matrice A comme le déterminant du système de ses vecteurs colonnes relativement à la base canonique. Il est noté det(A) puisqu'il n'y a pas d'ambiguïté sur la base de référence.
Par définition même, le déterminant dépend de façon linéaire de chaque colonne, et est nul lorsque deux colonnes sont égales. Le déterminant de la matrice identité vaut un. Enfin il vérifie la formule de Leibniz
Ce déterminant se note fréquemment avec des barres verticales :
La présentation matricielle apporte une propriété essentielle : une matrice a même déterminant que sa transposée
Ce qui signifie que le déterminant de A se voit aussi comme le déterminant du système des vecteurs lignes, relativement à la base canonique.
En appliquant la formule de Leibniz à la transposée
On effectue un changement d'indice en posant j = σ(i). Par bijectivité de σ, cela conduit à
Une deuxième réindexation s'impose : prendre τ = σ − 1. L'application qui à σ associe son inverse est une bijection de
Déterminant d'un endomorphisme
Soit u un endomorphisme d'un espace vectoriel de dimension finie. Toutes les matrices représentatives de u ont le même déterminant. Cette valeur commune est appelée déterminant de u.
Le déterminant de u est la valeur par laquelle u multiplie les déterminants de vecteurs
On introduit l'application du,B qui à x1, ..., xn associe
C'est une forme n-linéaire alternée et sa valeur sur les vecteurs de B, qu'on note du,B(B), est justement le déterminant de la matrice représentative de u dans la base B. La forme du,B est donc proportionnelle au déterminant en base B, le rapport de proportionnalité se calculant en prenant l'image des vecteurs de B
Ce qui signifie, pour un n-uplet de vecteurs
Notamment les endomorphismes de déterminant 1 conservent le déterminant des vecteurs. Ils forment un sous groupe de Gl(E), noté Sl(E), et appelé groupe spécial linéaire. Dans un espace réel de dimension deux, ils se conçoivent comme les applications linéaires conservant les aires orientées, en dimension trois les volumes orientés.
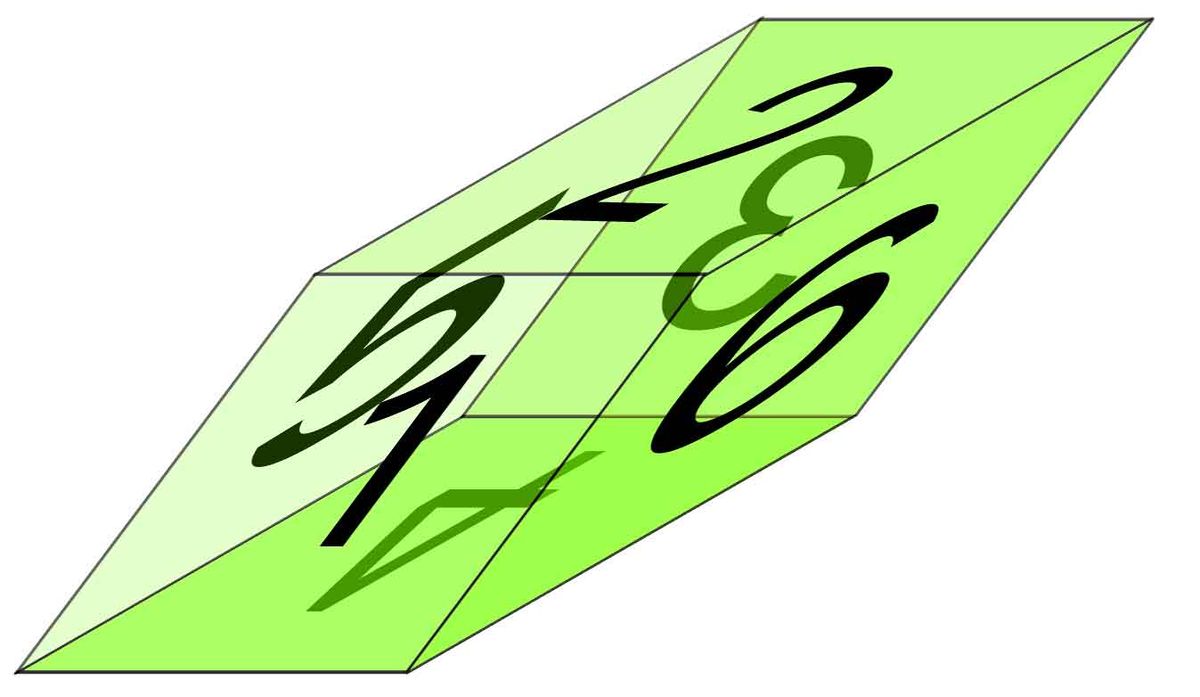
On démontre que ce groupe est engendré par les transvections, dont la matrice dans une base adaptée est de la forme
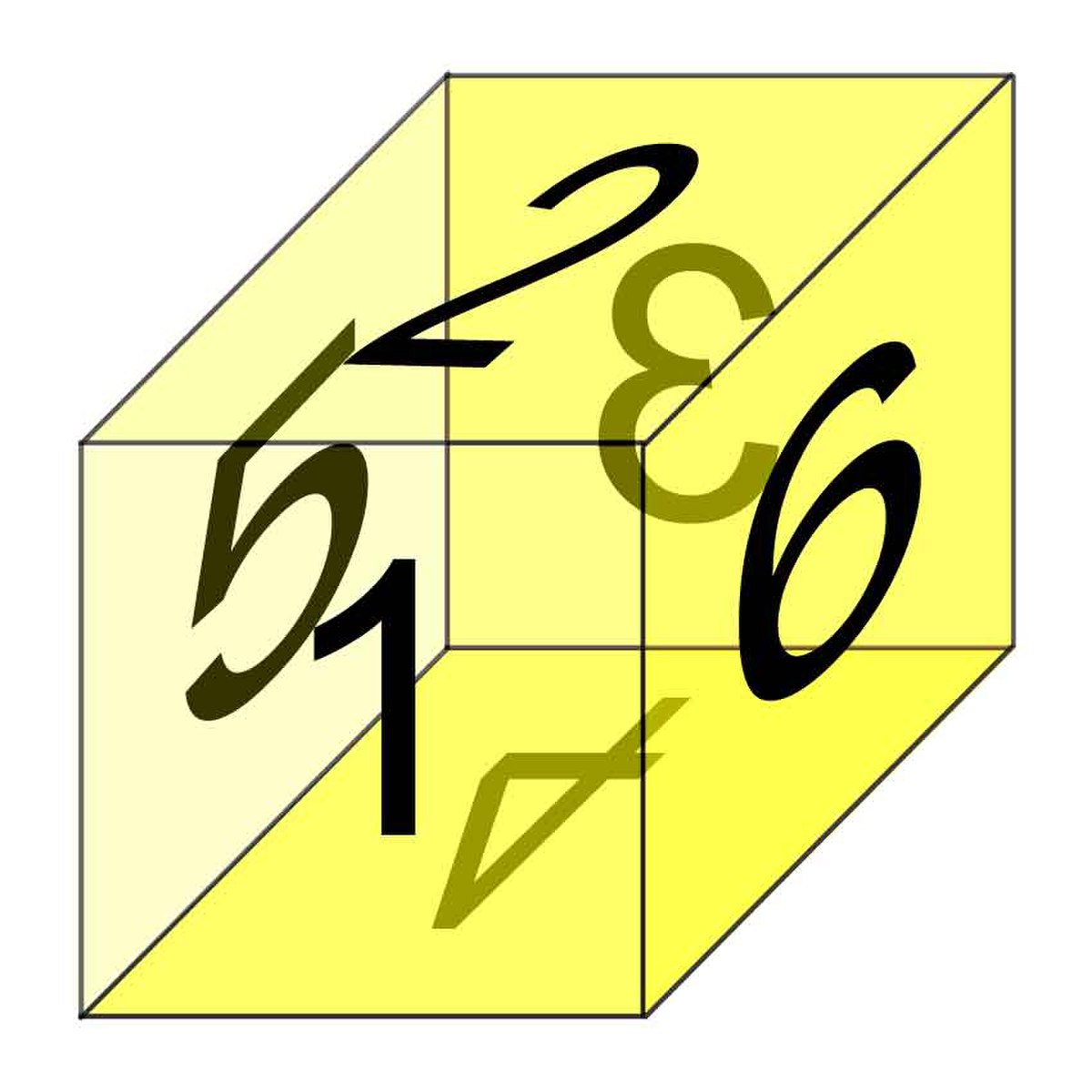
Fig. 8. Cube avant transvection |
Par construction même du déterminant des endomorphismes, deux matrices semblables ont même déterminant.
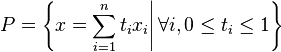
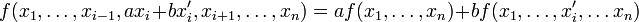
![[\exists i\neq j, x_i=x_j] \Rightarrow f(x_1,\dots, x_n)=0](https://static.techno-science.net/illustration/Definitions/autres/7/7b61ad4e932d79a43dd9d8b4470e915f_56326b098b651b8a817f98e9b4ecd433.png)