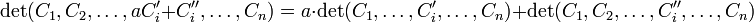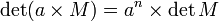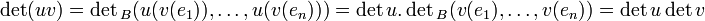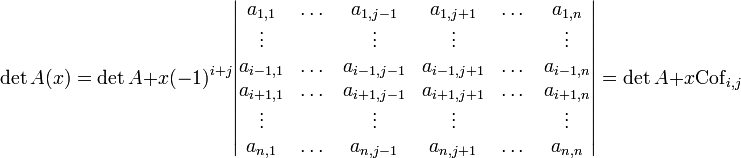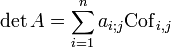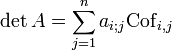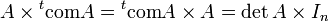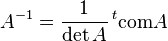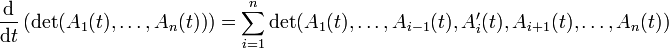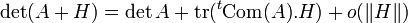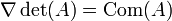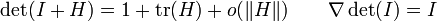Déterminant (mathématiques) - Définition

Propriétés

Quitte à effectuer le choix d'une base, il est possible d'énoncer ces propriétés dans le cadre matriciel.

Caractère n-linéaire alterné

L'application déterminant sur les familles de vecteurs est une forme multilinéaire alternée. Utiliser cette propriété sur une matrice demande d'exprimer le système de vecteurs colonnes, ou de vecteurs lignes.

Par exemple si la matrice A admet pour colonnes C₁, ..., C_n avec C_i de la forme C_i=aC '_i+C ' '_i

Voici l'effet des opérations élémentaires sur les colonnes de la matrice

• multiplier une colonne par a, entraîne la multiplication du déterminant par la même valeur
• échanger deux colonnes, entraîne la multiplication du déterminant par -1
• ajouter à une colonne une combinaison linéaire des autres colonnes ne modifie pas le déterminant.

Notamment, si toutes les colonnes sont multipliées par a, le résultat est une multiplication par aⁿ du déterminant

En revanche, il n'existe pas de formule simple exprimant le déterminant de la somme A+B de deux matrices. En effet, appliquer la multilinéarité par rapport aux colonnes demande d'écrire les colonnes de la somme comme A_i+B_i, puis d'appliquer n fois la propriété de linéarité. Finalement, le déterminant de A+B se scinde en une somme de 2ⁿ déterminants hybrides det(A₁, A₂, B₃, A₄,..., B_n), formés d'un certain nombre de colonnes de A et de B.

Il est possible d'effectuer également des opérations élémentaires sur les lignes, qui ont les mêmes propriétés que les opérations sur les colonnes. Opérer sur les lignes suivant la technique du pivot de Gauss fournit une méthode systématique de calcul des déterminants ; c'est la méthode la plus efficace en règle générale.

Propriétés de morphisme et d'annulation

Cas d'annulation des déterminants

• le déterminant d'un système de n vecteurs est nul si et seulement si ce système est lié (et ceci est valable quelle que soit la base de référence)
• le déterminant d'une matrice (ou d'un endomorphisme) est nul si et seulement si cette matrice (ou endomorphisme) est non inversible.

Ces propriétés expliquent le rôle essentiel que peuvent jouer les déterminants en algèbre linéaire. Ils constituent un outil fondamental pour prouver qu'une famille de vecteurs est une base.

Démonstration du cas d'annulation

• si le système est lié, une colonne est combinaison linéaire des autres. Par une opération élémentaire, il est possible de se ramener à un déterminant ayant une colonne nulle, donc nul.
• si le système est libre, il est possible de le considérer comme une base B' et lui appliquer la formule de changement de bases : det_B(B ').det_B ' (B)=1.

Propriété de morphisme

• 
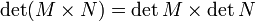
• ainsi si M est inversible alors
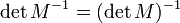
• et le déterminant est un morphisme de groupes de dans

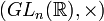
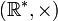
Démonstration de la propriété de morphisme

La double application de la formule pour l'image d'une famille de vecteurs donne le résultat, en prenant les vecteurs images des vecteurs de la base B eux-mêmes

Il existe une généralisation de la formule de déterminant d'un produit pour le cas de deux matrices rectangulaires : c'est la formule de Binet-Cauchy.

Cofacteurs et formule de récurrence

Soit A une matrice carrée de taille n, et A(x) la matrice dont les coefficients sont les mêmes que ceux de A, sauf le terme d'indice i, j qui vaut a_{i, j}+x (c'est la modification d'un des coefficients de la matrice, toutes choses égales par ailleurs). Par la formule de linéarité pour la j-ème colonne, il est possible d'établir

Le terme noté Cof_{i, j} est appelé cofacteur d'indice i, j. Il se calcule de la façon suivante : en notant M(i;j) le déterminant de la sous-matrice déduite de M par suppression la ligne i et la colonne j, le cofacteur est (-1)^i+j fois M(i;j).

Il admet les interprétations suivantes

• augmenter de x le coefficient d'indice i, j de la matrice (toutes choses égales par ailleurs) revient à augmenter le déterminant de x fois le cofacteur correspondant
• le cofacteur est la dérivée du déterminant de la matrice A(x)

Formules de Laplace

Si n>1 et A est une matrice carrée de taille n alors il est possible de calculer son déterminant en fonction des coefficients d'une seule colonne et des cofacteurs correspondants. Cette formule, dite formule de Laplace, permet ainsi de ramener le calcul du déterminant à n calculs de déterminants de taille n-1.

• Formule de développement par rapport à la colonne j

• On peut donner également une formule de développement par rapport à la ligne i

Comatrice et calcul de l'inverse

La comatrice de A, est la matrice constituée des cofacteurs de A. Elle généralise les formules de développement du déterminant par rapport aux lignes ou colonnes

La matrice transposée de la comatrice est appelée matrice complémentaire de A. Notamment si A est inversible, l'inverse de A est un multiple de la matrice complémentaire. Cette approche offre une formule de la matrice inverse, ne nécessitant que des calculs de déterminants

Variations de la fonction déterminant

La formule de Leibniz montre que le déterminant d'une matrice A s'exprime comme somme et produit de composantes de A. Il n'est donc pas étonnant que le déterminant ait de bonnes propriétés de régularité.

Déterminant dépendant d'un paramètre

Si est une fonction de classe à valeurs dans les matrices carrées d'ordre n, alors est également de classe .

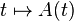
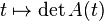
La formule de dérivation s'obtient en faisant intervenir les colonnes de A

Cette formule est formellement analogue à la dérivée d'un produit de n fonctions numériques.

Application déterminant sur l'espace des matrices

• L'application qui à la matrice A associe son déterminant est continue.

Cette propriété présente des conséquences topologiques intéressantes : ainsi le groupe GL_n( ) est un ouvert, la loi de multiplication des matrices en fait un groupe de Lie, et le sous-groupe est un fermé dans GL_n( ).

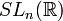
• Cette application est différentiable et même .

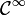
Le développement limité à l'ordre un du déterminant au voisinage de A s'écrit

C'est-à-dire que dans muni de son produit scalaire canonique, la comatrice s'interprète comme le gradient de l'application déterminant

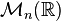
Notamment pour le cas où A est l'identité

Le caractère différentiable permet d'affirmer que est aussi un groupe de Lie.

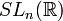
• Elle est aussi polynomiale, ce qui fait de GL_n( ) une variété algébrique.

Ces formules portent parfois le nom d'identités de Jacobi. Elles sont établies dans l'article comatrice.