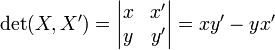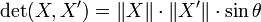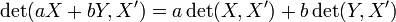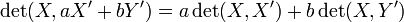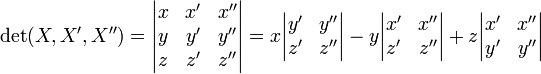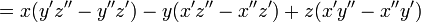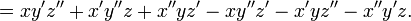Déterminant (mathématiques) - Définition

Premiers exemples : aires et volumes

Les calculs d'aires et de volumes sous forme de déterminants dans des espaces euclidiens apparaissent comme des cas particuliers de la notion plus générale de déterminant. Pour les distinguer, la lettre majuscule D (Det) leur est parfois réservée.

Déterminant de deux vecteurs dans le plan euclidien

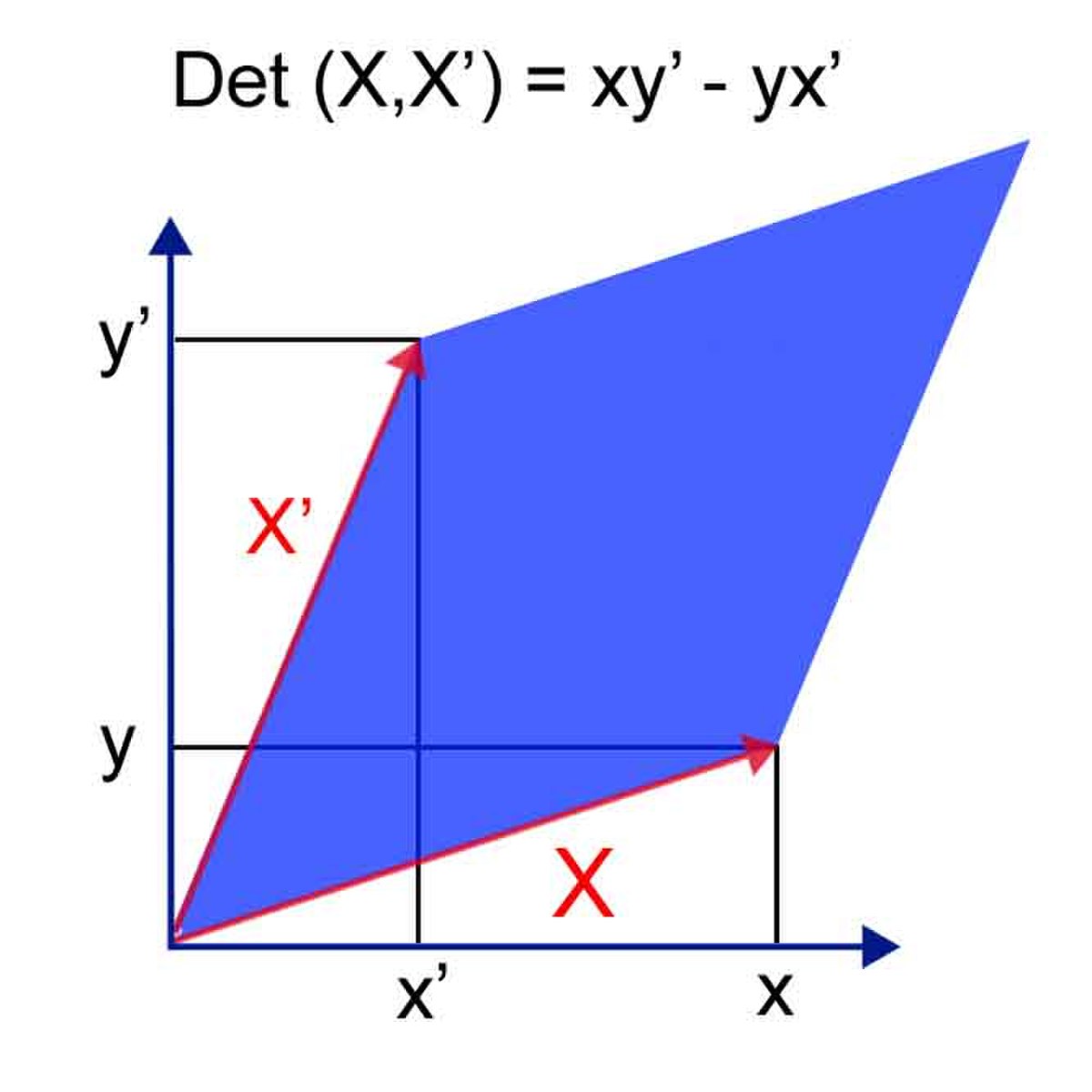
Soit P le plan euclidien orienté usuel. Le déterminant des vecteurs X et X' est donné par l'expression analytique

ou, de façon équivalente, par l'expression géométrique

dans laquelle θ est l'angle orienté formé par les vecteurs X et X'.

Propriétés

• La valeur absolue du déterminant est égale à l'aire du parallélogramme défini par X et X' (X'sinθ est en effet la hauteur du parallélogramme, d'où Aire = Base × Hauteur).
• Le déterminant est nul si et seulement si les deux vecteurs sont colinéaires (le parallélogramme devient une ligne).

En effet cette annulation apparaît comme un simple test de proportionnalité des composantes des vecteurs par produit en croix.

• Son signe est strictement positif si et seulement si la mesure de l'angle (X,X') est comprise dans l'intervalle ]0,π[.
• L'application déterminant est bilinéaire : la linéarité par rapport au premier vecteur s'écrit

et celle par rapport au second vecteur s'écrit

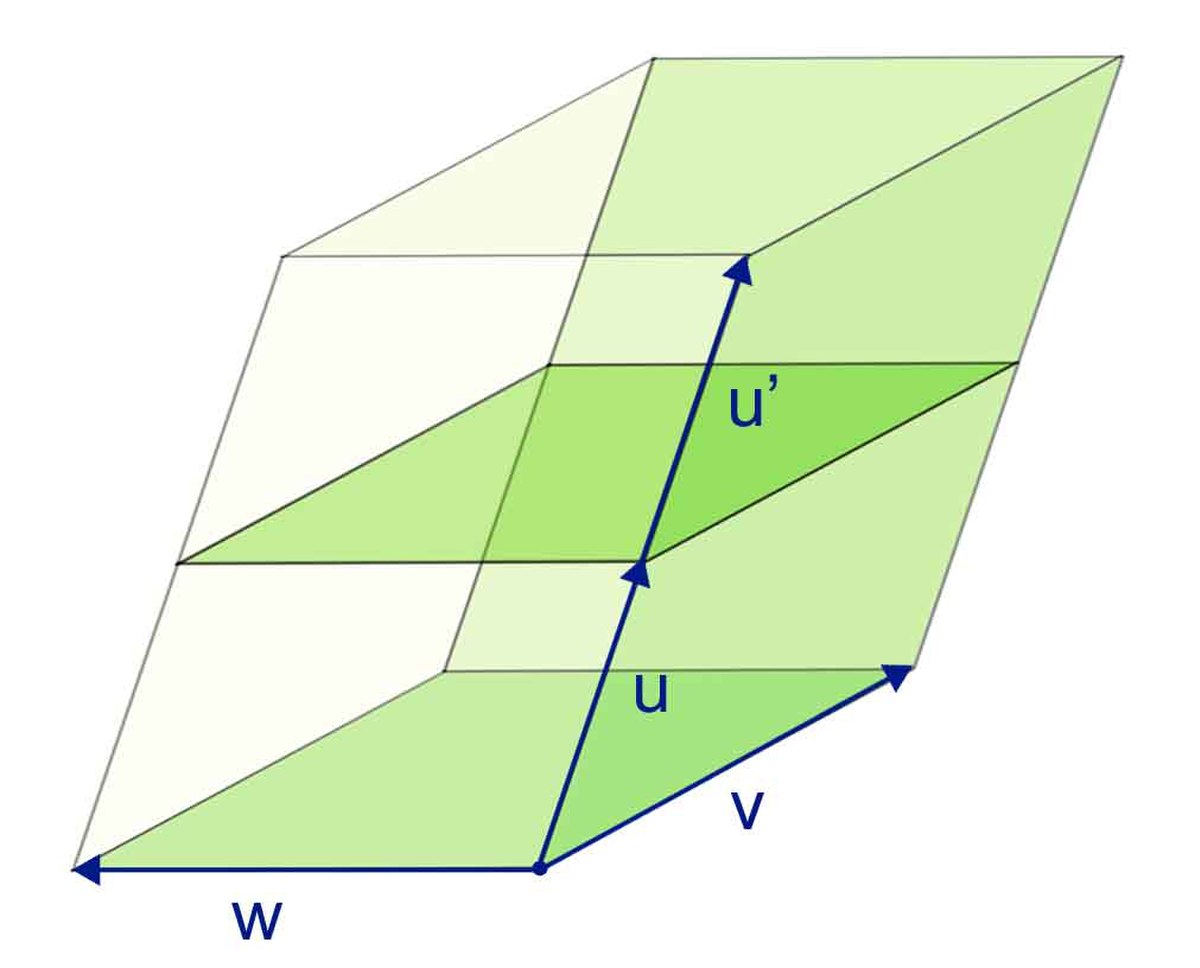
La figure 2, dans le plan, illustre un cas particulier de cette formule. Elle représente deux parallélogrammes adjacents, l'un défini par les vecteurs u et v (en vert), l'autre par les vecteurs u' et v (en bleu). Il est aisé de visualiser sur cet exemple l'aire du parallélogramme défini par les vecteurs u+u' et v (en gris) : elle est égale à la somme des aires des deux parallélogrammes précédents, à laquelle est enlevée l'aire d'un triangle, et ajoutée l'aire d'un autre triangle. Les deux triangles se correspondant par translation, la formule suivante est vérifiée det(u + u',v) = det(u,v) + det(u',v).

Ce dessin correspond à un cas particulier de la formule de bilinéarité puisque les orientations ont été choisies de façon à ce que les aires aient le même signe, mais il aide à en saisir le contenu géométrique.

Généralisation

Il est possible de définir la notion de déterminant dans un plan euclidien orienté muni d'une base orthonormale directe B, en utilisant les coordonnées des vecteurs dans cette base. Le calcul de déterminant donne le même résultat quelle que soit la base orthonormale directe choisie pour le calcul.

Déterminant de trois vecteurs dans l'espace euclidien

Soit E l'espace euclidien orienté usuel de dimension 3. Le déterminant de trois vecteurs de E est donné par

Ce déterminant porte encore le nom de produit mixte ; la formule de calcul correspondante est connue sous le nom de règle de Sarrus.

Propriétés

• La valeur absolue du déterminant est égale au volume du parallélépipède défini par les trois vecteurs.
• Le déterminant est nul si et seulement si les trois vecteurs sont contenus dans un même plan (parallélépipède « plat »).
• L'application déterminant est trilinéaire : notamment

det(aX + bY,X',X'') = adet(X,X',X'') + bdet(Y,X',X'')

Une illustration géométrique de cette propriété est donnée en figure 3, par deux parallélépipèdes adjacents, c'est-à-dire possédant une face commune. L'égalité suivante devient intuitive

det(u + u',v,w) = det(u,v,w) + det(u',v,w).

Interprétation du signe du déterminant : orientation

Dans le plan, le signe du déterminant s'interprète comme le signe de l'angle orienté.

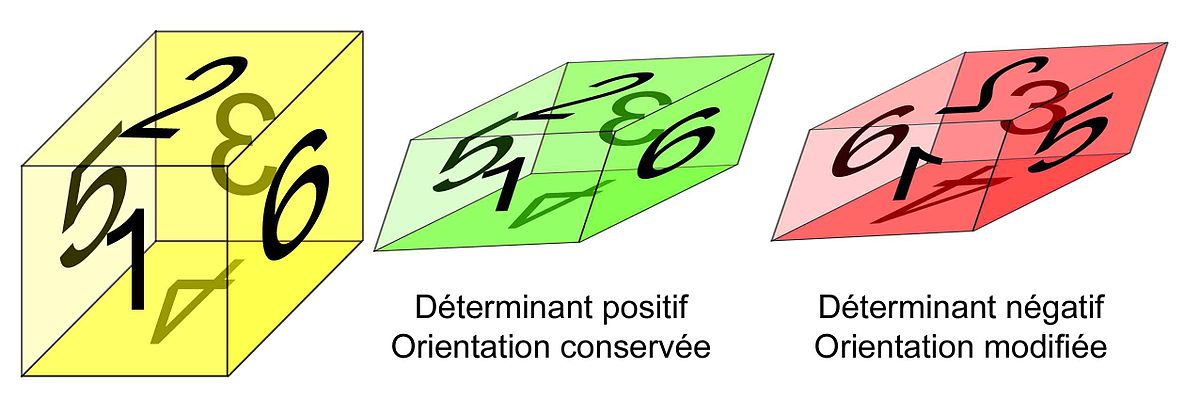
Dans l'espace à trois dimensions, le cube unité sert de référence. Son déterminant vaut un. Un parallélépipède non plat possède un déterminant positif s'il est possible de l'obtenir en déformant continûment, sans jamais l'aplatir, le cube unité.

Le déterminant est au contraire négatif s'il est nécessaire d'appliquer en plus une symétrie, c’est-à-dire si le cube unité ne peut être obtenu qu'en déformant le parallélépipède, puis en observant le résultat de cette déformation dans un miroir.

Approche intuitive du déterminant d'une application linéaire

Une application linéaire est une application qui transforme les coordonnées d'un vecteur de manière linéaire. Par exemple dans l'espace de dimension 3, l'application est linéaire si les coordonnées x, y et z d'un vecteur ont pour image x', y' et z' avec :

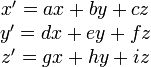
où a, b,c,..., i sont des nombres. La figure suivante illustre deux cas de telles applications linéaires.

Dans le premier cas, le cube jaune est transformé en un parallélépipède illustré en vert. Dans le deuxième cas, le cube jaune est transformé en un volume aplati, un carré rouge (c'est-à-dire que certains des sommets du cube initial ont la même image par l'application linéaire). Ces deux cas correspondent à des situations différentes en mathématique. La première fonction du déterminant est de fournir un moyen de séparer ces cas.

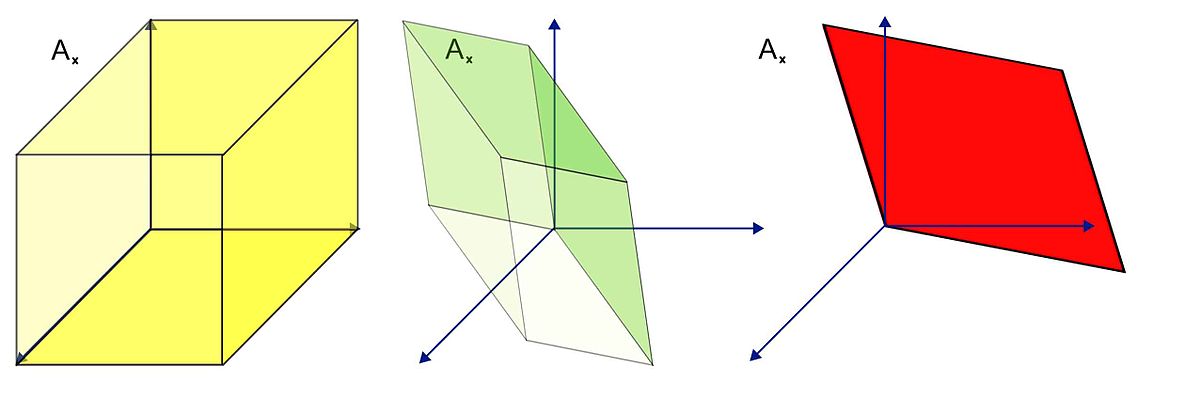
Pour être plus précis, le déterminant d'une application linéaire est un nombre, qui représente un facteur multiplicatif pour les volumes. Si le cube jaune est de volume 1, alors le volume de l'image du cube vert est la valeur absolue du déterminant de la première application. La deuxième application a un déterminant nul, ce qui correspond à un aplatissement des volumes.

Le signe du déterminant est positif s'il est possible de déformer continûment le cube jaune pour obtenir le vert. Il est au contraire négatif s'il est nécessaire d'y appliquer en plus une symétrie.

En fait cette propriété n'est pas uniquement vraie pour le cube unité jaune. Tout volume transformé par une application linéaire est multiplié par la valeur absolue du déterminant.

Le déterminant existe pour les applications linéaires d'un espace dans lui même dans le cas de toutes les dimensions finies. En effet, la notion de volume peut être généralisée : ainsi un « hypercube » ayant ses arêtes de longueur 2 dans un espace euclidien de dimension n aurait un déterminant (sorte d'« hypervolume ») de 2ⁿ. En revanche si l'espace contient une infinité de dimensions, alors le déterminant n'a plus de sens.