Déterminant (mathématiques) - Définition

Cadre d'utilisation

Déterminant et équations linéaires

Il existe un cas de calcul numérique très fréquent pour les ingénieurs, les physiciens ou les économistes. Il s'agit de la résolution d'un système d'équations linéaires. Si le système possède autant d'équations que de variables, on peut espérer avoir l'existence et l'unicité d'une solution. Mais ce n'est pas toujours le cas, par exemple en cas de répétition de la même équation, plusieurs solutions conviendront.

Plus précisément, à un système de n équations et n inconnues peut être associé un déterminant. L'existence et l'unicité de la solution est obtenue si et seulement si le déterminant est différent de 0. Ce problème est l'origine historique de l'introduction des déterminants.

Il est possible, non seulement de garantir l'existence et l'unicité de la solution, mais la règle de Cramer fournit un calcul exact de la solution à l'aide de déterminants. Cette méthode n'est ni la plus rapide, ni la plus simple, elle est peu pratiquée pour les calculs explicites, elle est néanmoins utile pour établir certains résultats théoriques, telle que la dépendance par rapport aux paramètres.

Lien avec l'aplatissement des volumes

Un système de 3 équations linéaires à 3 inconnues peut être mis sous forme d'une équation linéaire u(X)=B où X=(x, y,z) est un vecteur dont les composantes sont les inconnues du système, u une application linéaire de l'espace et B un vecteur. La résolution du système peut être formulée de façon géométrique : le vecteur B est-il l'image d'un certain vecteur X par u ? Ce dernier est-il unique ? Le déterminant de u apporte la réponse : l'existence et l'unicité sont obtenues si et seulement s'il est non nul.

La figure 5 permet une approche intuitive de ce résultat. Il suffit de considérer un pavage de l'espace par le cube jaune et ses images par des translations selon les trois directions. Une famille de cubes jaunes adjacents remplissent alors tout l'espace.

• Si le déterminant n'est pas nul, alors l'image de ce pavage est un pavage de parallélépipèdes de couleur verte, remplissant également tout l'espace. Ceci signifie que tous les vecteurs de l'espace sont des vecteurs images. Notamment, l'inconnue est bien recouverte par l'un des volumes verts. Elle est image d'un vecteur.
• En revanche, si le déterminant est nul, alors l'image du pavage ne remplit pas l'espace entier. Dans l'exemple du cube aplati rouge, elle ne remplit qu'un plan. Certains vecteurs ne sont jamais atteints, les autres sont l'image de plusieurs vecteurs à la fois.

Plus généralement, pour un système de n équations et n inconnues, le déterminant indique si les images par u remplissent l'espace entier ou seulement un sous-espace.

Déterminant et réduction

Les applications linéaires apparaissent non seulement en géométrie élémentaire mais aussi dans de nombreux domaines avancés comme certaines résolutions d'équations différentielles, la définition d'algorithmes rapides ou la résolution de problèmes théoriques. Il est important de comprendre leur comportement.

Un outil d'analyse fécond consiste à répertorier les axes privilégiés, selon lesquels l'application se comporte comme une dilatation, multipliant les longueurs des vecteurs par une constante. Ce rapport de dilatation est appelé valeur propre et les vecteurs auxquels il s'applique vecteurs propres.

Le phénomène d'aplatissement des volumes peut être mesuré par un déterminant. Il correspond au cas où, selon une certaine direction, les vecteurs sont multipliés par un rapport de dilatation égal à 0 (valeur propre nulle). Plus généralement, toutes les valeurs propres peuvent être obtenues par le calcul d'un déterminant à paramètre, appelé polynôme caractéristique.

Déterminant et intégrale multiple

Fig. 6. Jacobien.

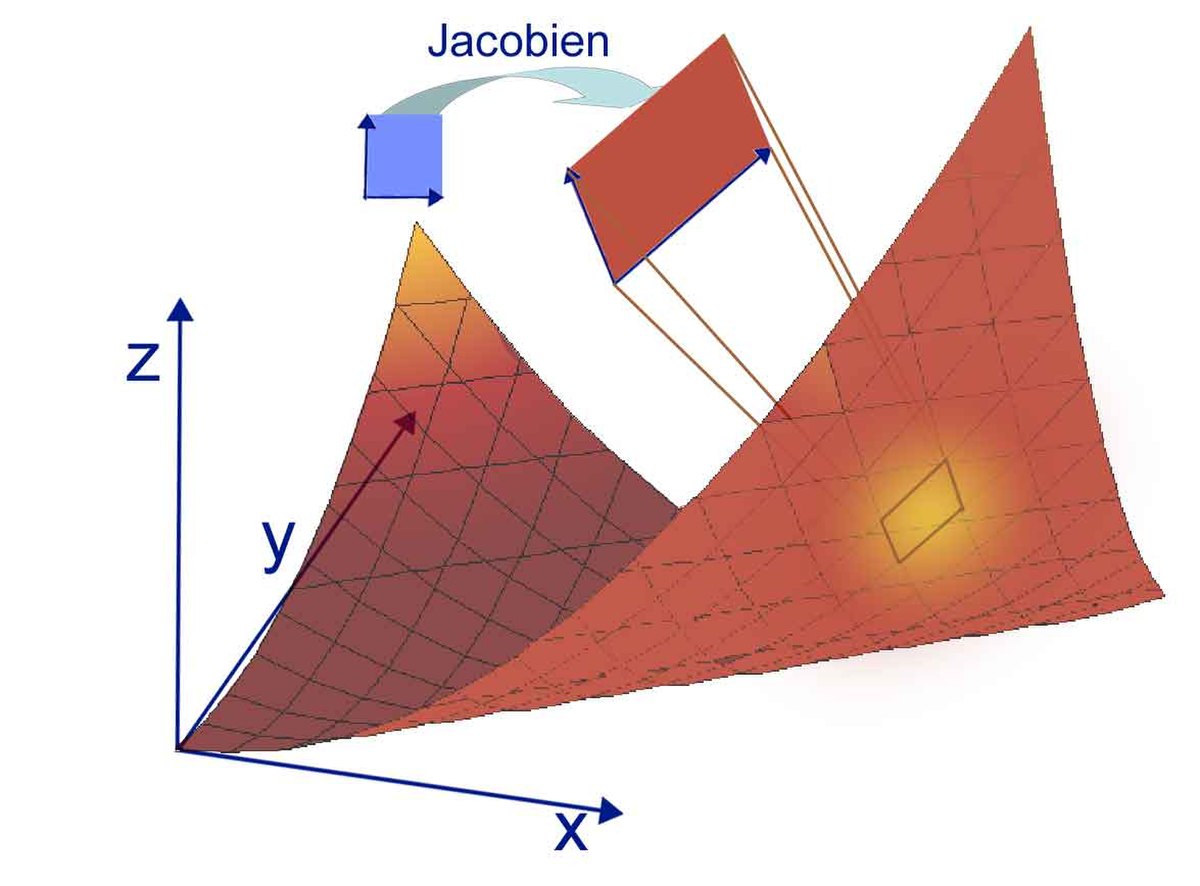
Ainsi que le montre l'approche intuitive, le déterminant caractérise la modification de volume d'un parallélépipède par un endomorphisme. L'intégrale multiple est un outil de détermination des volumes dans le cas général. Elle utilise la notion de déterminant dans le cadre du changement de variables. Il prend alors le nom de jacobien. Il peut être imaginé comme le rapport des volumes élémentaires avant et après changement de variables, en usant de la terminologie des éléments différentiels.

Plus précisément, le comportement d'une application différentiable au voisinage d'un point est au premier ordre, analogue en termes de modification de volume, à une application linéaire ayant comme déterminant le jacobien.

Déterminant et amortissement dans les équations différentielles

Fig. 7. Exemple du pendule de longueur variable, sans amortissement. En bleu et en rouge sont représentées deux solutions particulières, dans l'espace des phases. L'aire formée par les deux solutions reste constante au cours du temps

En physique, notamment en mécanique du point, l'équation différentielle linéaire d'ordre deux est fréquente. Elle se présente sous la forme y'' = ay' + by + c, dans laquelle a,b,c peuvent être des coefficients constants ou plus généralement des fonctions (par exemple du temps). Le terme a est appelé facteur d'amortissement.

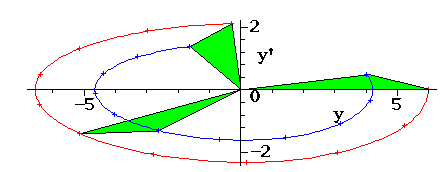
Cette équation différentielle est associée à un déterminant, appelé wronskien. Il s'interprète comme une aire dans le plan (y, y') appelé espace des phases par les physiciens. Cette aire reste constante au cours du temps si le terme d'amortissement est nul, elle décroît de façon exponentielle s'il est strictement positif. S'il n'est pas toujours possible d'exhiber une solution explicite, le wronskien est toujours calculable.

Le wronskien peut être généralisé à toutes les équations différentielles linéaires.