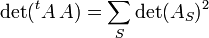Déterminant de Gram - Définition
La liste des auteurs de cet article est disponible ici.
Interprétation géométrique
Calcul des volumes de parallélotopes
Le calcul de la distance à un sous-espace permet de montrer par récurrence que le déterminant de Gram d'une famille de n vecteurs est égal au carré du volume euclidien du parallélotope correspondant.
Pour n=1 c'est bien le cas car
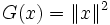
En supposant la propriété vraie pour toute famille de n vecteurs, on l'établit pour n+1. La distance de xn+1 à F espace engendré par les n premiers vecteurs est le carré de la hauteur du parallélotope, et G(x1, ..., xn) est le carré du volume de la base par hypothèse de récurrence.
Le volume s'obtient donc en prenant la racine carrée du déterminant de Gram, sans qu'il soit possible de lui donner un signe (pour plus de détails sur cette dernière question, consulter l'article orientation).
Application de la formule de Binet-Cauchy
La formule de Binet-Cauchy montre comment le volume d'un parallélotope de dimension d dans un espace de dimension n peut être ramené au calcul de volumes de projections orthogonales du parallélotope sur des sous-espaces de coordonnées. Elle s'écrit
dans cette expression S décrit les différents sous-ensembles à d éléments de l'ensemble { 1, ..., n }. Pour chaque S, la matrice AS est la matrice carrée de taille d obtenue en ne retenant que les colonnes de A dont l'indice appartient à S.
La formule de Binet-Cauchy montre que le carré du volume du parallélotope est égal à la somme des carrés des volumes des projections orthogonales sur les différents sous-espaces de coordonnées de dimension m (qui sont au nombre de
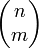
Dans le cas m=1, ces projections orthogonales sont des segments, et on retrouve une forme du théorème de Pythagore.
Espace euclidien • Espace hermitien • Forme bilinéaire • Forme quadratique • Forme sesquilinéaire • Orthogonalité • Base orthonormale • Projection orthogonale • Inégalité de Cauchy-Schwarz • Inégalité de Minkowski • Matrice positive • Matrice définie positive • Décomposition QR • Déterminant de Gram • Espace de Hilbert • Base de Hilbert • Théorème spectral • Théorème de Stampacchia • Théorème de Riesz • Théorème de Lax-Milgram • Théorème de représentation de Riesz