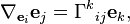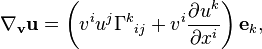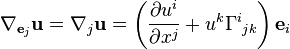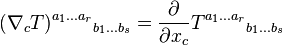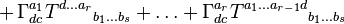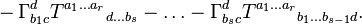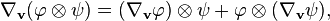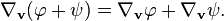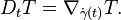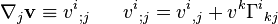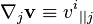Dérivée covariante - Définition
La liste des auteurs de cet article est disponible ici.
Description en coordonnées
Champ de vecteurs
Soit des coordonnées
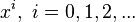
Les coefficients Γki j sont appelées les symboles de Christoffel.
En utilisant ces coefficients pour des vecteurs
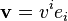
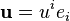
Le premier terme de cette formule décrit la « déformation » du système de coordonnées par rapport à la dérivée covariante, et le second les changements de coordonnées du vecteur u. En particulier
La dérivée covariante est la dérivée selon les coordonnées à laquelle on ajoute des termes correctifs décrivant l'évolution des coordonnées.
Champ de tenseurs
La dérivée covariante d'un tenseur de type (r,s) par rapport à ec est donnée par l'expression :
Définition formelle
Fonctions
Pour une fonction f, la dérivée covariante
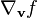
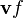
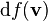
Champ de vecteurs
Une dérivée covariante

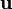
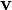
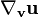
-
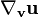
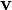
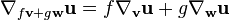
-
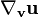
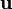
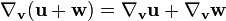
-
![\nabla_{\mathbf u} {\mathbf v} - \nabla_{\mathbf v} {\mathbf u} = [\mathbf u, \mathbf v]](https://static.techno-science.net/illustration/Definitions/autres/e/eee6333299cb64e0262acf3020c39f72_148aa468df864ff82f3eefbe8d94bfb7.png)
![[\mathbf u, \mathbf v]](https://static.techno-science.net/illustration/Definitions/autres/6/683edb00212ef113649d0bd37b69ccb4_db935079b62bf7be97b7b50ec817e66e.png)
-
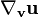
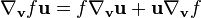
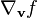
Noter que
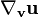
Champ de tenseurs
Une fois que la dérivée covariante est définie pour les champs de vecteurs, elle peut être étendue aux champs tensoriels en utilisant les identités suivantes où

et si

La dérivée covariante d'un champ de tenseurs le long d'un vecteur v est à nouveau un champ de tenseur du même type.
Dérivée le long d'une courbe
Du fait que la dérivée covariante
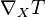
Dans ce cas le champ tensoriel T doit être défini simplement le long de la courbe γ(t).
Parfois la dérivée covariante le long d'une courbe est qualifiée d'absolue ou dérivée intrinsèque.
Notation
Dans les ouvrages de physique, la dérivée covariante est parfois décrite à l'aide de ses composantes dans les équations.
On note souvent la dérivée covariante à l'aide d'un point-virgule, tandis que la dérivée partielle usuelle est indiquée par une virgule, sur le modèle suivant :
À nouveau, ceci montre que la dérivée covariante d'un champ vectoriel n'est pas simplement obtenue en dérivant les coordonnées vi,j, mais dépend aussi du vecteur v lui-même à travers vkΓikj.
Dans d'autres textes plus anciens (incluant l'ouvrage Introduction to General Relativity, Adler, Bazin & Schiffer), la dérivée covariante est notée à l'aide d'une double barre verticale :