Densité de probabilité - Définition
La liste des auteurs de cet article est disponible ici.
Fonction de variables aléatoires à densité
Dans cette section, on considère la question suivante : étant donnée une variable aléatoire

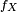
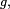
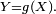
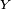
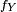
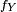
Somme de variables aléatoires indépendantes
La densité de probabilité de la somme de deux variables aléatoires indépendantes U et V, chacune ayant une densité fU et fV, est donnée par une convolution de ces densités:
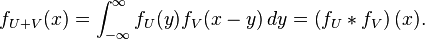
Dans cet exemple,
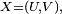
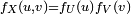
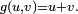
Dans cet exemple,
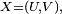
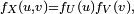
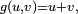
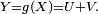

![\begin{align}\mathbb{E}[\varphi(Y)] &= \mathbb{E}[\varphi(U+V)] = \int_{\mathbb{R}^{2}}\varphi(u+v)f_{X}(u,v)dudv \\ &= \int_{\mathbb{R}^{2}}\varphi(y)f_{X}(t,y-t)\ |J(y,t)|\ dydt, \end{align}](https://static.techno-science.net/illustration/Definitions/autres/5/58e659ca6f6664c051f6e99b599795c9_f8a50e0c99c603d17c2991a5e0971cf2.png)
où
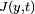
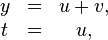
c'est-à-dire
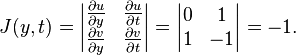
Donc, pour toute fonction

![\begin{align}\mathbb{E}[\varphi(Y)] &= \int_{\mathbb{R}}\varphi(y)\left(\int_{\mathbb{R}}f_{X}(t,y-t)dt\right)\ dy \\ &= \int_{\mathbb{R}}\varphi(y)\left(\int_{\mathbb{R}}f_{U}(t)f_{V}(y-t)dt\right)\ dy \\ &= \int_{\mathbb{R}}\varphi(y)\ (f_{U}\ast f_{V})(y)\ dy. \end{align}](https://static.techno-science.net/illustration/Definitions/autres/0/0d6f34e0e187b8027f018f4e2184e0a1_f45e721264a98a9062df6361ea162b4e.png)
Pour déterminer la loi de la somme de variables indépendantes, on peut aussi passer par la fonction génératrice des moments ou par la fonction caractéristique d'une variable aléatoire . C'est ainsi qu'est démontré le théorème de la limite centrale.
Fonction d'une variable aléatoire réelle à densité
Notons
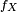
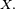
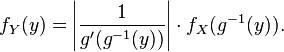
où g−1 représente la fonction réciproque de g et g' la dérivée de g.
Ce résultat découle du fait que les probabilités sont invariantes par changement de variable. Supposons par exemple que g est décroissante :
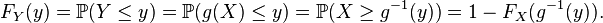
En différenciant, on obtient
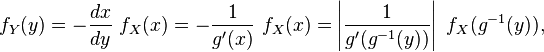
qui s'écrit encore
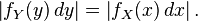
Le cas où g est croissante se traite de manière analogue.
Pour une transformation g non monotone, la densité de probabilité de Y est
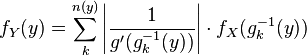
où n(y) est le nombre de solutions en x de l'équation g(x) = y, et
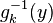
- Prenons l'exemple d'une fonction affine ; si
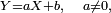
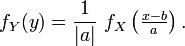
- En effet, si, par exemple, a est strictement négatif, on obtient, via le changement de variable
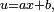
![\begin{align} \mathbb{E}[\varphi(Y)] &= \mathbb{E}[\varphi(aX+b)] = \int_{\mathbb{R}}\varphi(ax+b)f_X(x)dx \\ &= \int_{+\infty}^{-\infty}\varphi(u)f_X\left(\tfrac{u-b}{a}\right)\ \tfrac{du}{a} \\ &= \int_{-\infty}^{+\infty}\varphi(u)\ \left(\tfrac{1}{-a}\ f_X\left(\tfrac{u-b}{a}\right)\right)\ du, \end{align}](https://static.techno-science.net/illustration/Definitions/autres/0/023785808dca259070f0912bb3e07098_a7dbeab5804bb977b043d2d4cb58183b.png)
- ceci pour toute fonction

- Prenons l'exemple du carré d'une variable aléatoire ; on sait que, si
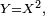
![\begin{align} \mathbb{E}[\varphi(Y)] &= \mathbb{E}[\varphi(X^2)] = \int_{\mathbb{R}}\varphi(x^2)f_X(x)dx \\ &= \int_{-\infty}^{0}\varphi(x^2)f_X(x)dx+\int_{0}^{+\infty}\varphi(x^2)f_X(x)dx \\ &= \int_{+\infty}^{0}\varphi(u)f_X(-\sqrt{u})\ \left(-\frac{du}{2\sqrt{u}}\right)+ \int_{0}^{+\infty}\varphi(u)f_X(\sqrt{u})\ \left(\frac{du}{2\sqrt{u}}\right) \\ &= \int_{\mathbb{R}}\varphi(u)\ \frac{1}{2\sqrt{u}} \left[f_X(\sqrt{u}) + f_X(-\sqrt{u})\right] 1_{u>0}du, \end{align}](https://upload.wikimedia.org/math/9/7/b/97b3bf70bc2085cf9046944027fa9af8.png)
- ceci pour toute fonction

![f_Y(y) = \frac{1}{2\sqrt{y}} \left[f_X(\sqrt{y}) + f_X(-\sqrt{y})\right] 1_{y>0}](https://upload.wikimedia.org/math/8/c/7/8c722d52895b73c91fff912f369494ae.png)
- ce qui est conforme à la formule.
- Autre solution : on sait que,
- si
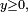
- si
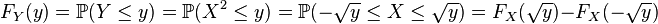
-
- si
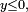
- si
- En dérivant, on trouve à nouveau
![f_Y(y) = \frac{1}{2\sqrt{y}} \left[f_X(\sqrt{y}) + f_X(-\sqrt{y})\right] 1_{y>0}.](https://upload.wikimedia.org/math/a/b/e/abeaf0a1897715a264d8b112e3929fdd.png)
Prenons X uniforme sur [0,2] et
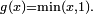
![P_Y(dy) = \tfrac12\ 1_{[0,1]}(y)\ dy\ +\ \tfrac12\ \delta_{1}(dy).](https://static.techno-science.net/illustration/Definitions/autres/b/b2aa00436a4cd524bb257d23d2d55261_c5a05c495db3717dc885a57c45ebbcf8.png)
Autrement dit, la loi de Y a une partie à densité, mais aussi un atome en 1.

















































