Degré de liberté (mécanique) - Définition
La liste des auteurs de cet article est disponible ici.
Tableau récapitulatif
Présentation
Le tableau ci-dessous récapitule, pour l'ensemble des liaisons mécaniques, le propos tenu ci-dessus. Toutes les liaisons sont supposées parfaites, sinon ce qui suit peut être inexact. Il faut encore une fois prendre des précautions pour passer de la simple matrice des degrés de liberté à la détermination des termes nuls d'un torseur. Le choix du point de réduction n'est pas toujours trivial; il faut une bonne connaissance des propriétés géométriques des liaisons pour en saisir la subtilité.
Les torseurs sont exprimés la plupart du temps au point A centre de la liaison. Le repère est le même que celui proposé dans l'article liaison mécanique. L'ensemble des autres points où la forme du torseur est semblable est indiqué en bas de chaque case.
La dernière colonne donne une illustration de la réalisation d'une liaison par association de ponctuelles.
| Nom liaison | Nb degré de liberté (de liaison) | Matrice des degrés de liberté | Torseur des efforts transmissibles
| torseur cinématiquement admissible
| Association de ponctuelles |
|---|---|---|---|---|---|
| liaison nulle | 6 (0) |
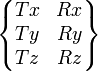
|
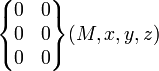
pour tout M |
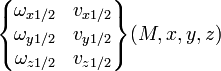
pour tout M |

|
| Liaison ponctuelle en A de normale(A,x) | 5 (1) |
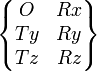
|
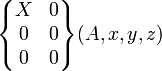
pour tout M∈(A,x) |
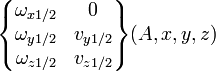
pour tout M∈(A,x) |

|
| Linéaire annulaire (A,x) | 4 (2) |
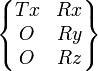
|
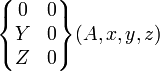
|
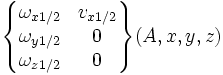
|

|
| Linéaire rectiligne Ligne (A,x) et normale de contact Y | 4 (2) |
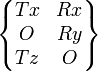
|
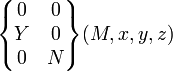
pour tout M∈Plan(A,x,y) |
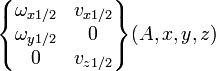
pour tout M∈Plan(A,x,y) |

|
| Appui plan (⊥x) | 3 (3) |
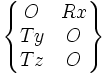
|
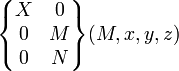
pour tout M |
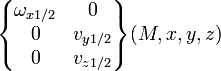
pour tout M |

|
| Rotule de centre A | 3 (3) |
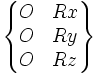
|
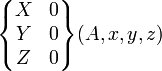
|
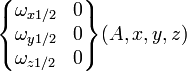
|

|
| Rotule à doigt de centre A (-Rx) | 2 (4) |
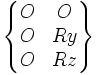
|
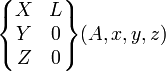
|
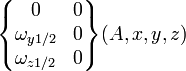
|

|
| Pivot glissant (A,x) | 2 (4) |
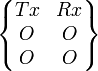
|
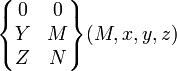
pour tout M∈(A,x) |
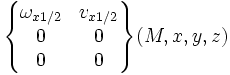
pour tout M∈(A,x) |

|
| Pivot (A,x) | 1 (5) |
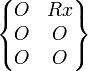
|
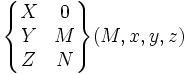
pour tout M∈(A,x) |
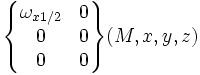
pour tout M∈(A,x) |

|
| Glissière hélicoïdale (A,x) | 1 (5) |
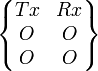
Avec Tx= k. Rx |
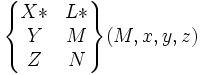
pour tout M∈(A,x) (*) voir ci-dessous |
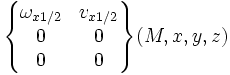
pour tout M∈(A,x) |

|
| Glissière (X) | 1 (5) |
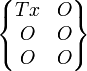
|
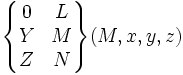
pour tout M |
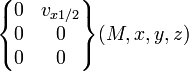
pour tout M |

|
| Complète | 0 (6) |
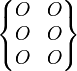
|
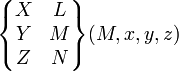
pour tout M |
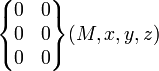
pour tout M |

|
Cas particulier de la liaison hélicoïdale
Dans cette liaison deux degrés de liberté semblent subsister. Cela provient du fait que les 6 mouvements élémentaires ne permettent pas de l'écrire autrement. Cependant à travers cette liaison, un seul mouvement est possible, puisqu'on ne peut pas effectuer la translation seule ou la rotation seule.
Ce cas illustre bien le danger qu'il y a à considérer les degrés de liberté pour la détermination des torseurs cinématiques ou statique dans une liaison.
La relation cinématique entre les deux mouvements, induit donc (par dualité des torseurs) une relation entre la poussée axiale (Force) et le moment autour de l'axe (ou couple).
Il suffit de comparer dans le tableau ci-dessus les modèles par ponctuelles des pivot, glissière et glissière hélicoïdale pour constater qu'il s'agit d'une seule et même solution. Seule diffère l'inclinaison de la 5e ponctuelle par rapport à l'axe du pivot glissant constitué par les 4 autres.
Liaison nulle et liaison complète
La base du repère de liaison et le point de réduction des torseurs n'ont aucune importance pour ces deux cas.
La liaison nulle est sans intérêt sur le plan mécanique mais son étude mathématique est semblable à celle des autres liaisons.
La liaison compète peut sembler sans intérêt, du moins cinématiquement, puisqu'aucun mouvement n'est permis. Toutefois en statique, son torseur d'action mécanique fait l'objet d'attention particulière, en construction mécanique puisqu'il renseigne sur la direction des efforts transmis par la liaison.
En résistance des matériaux le torseur de cohésion représente les efforts subit dans une section de poutre. Il s'agit d'une liaison complète entre deux parties d'une même pièce. Cette étude aboutit au dimensionnement de la pièce au regard des charges appliquées.
Pour un système rigide, aucun mouvement n'étant possible, les efforts de liaison ont évidemment une puissance nulle !