Définition d'écran - Définition
La liste des auteurs de cet article est disponible ici.
Relations entre la définition et la résolution physique d'un écran et la résolution observée
La définition d’écran exprimant aussi la surface d’un seul pixel plan, elle influe sur la qualité perçue de l'image selon la distance à laquelle on l'observe, car ce pixel est alors seulement perçu selon un angle solide du cône d’observation, qu’on devait exprimer en stéradians.
Cependant on peut aussi se contenter de mesurer l’ouverture du cône en radians, en ne mesurant que l’arc angulaire d’une coupe plane de ce cône le long de la direction d’observation. À une distance suffisamment grande par rapport à la largeur ou la hauteur d’un pixel, cet arc angulaire est pratiquement égal à la hauteur ou la largeur de chaque pixel, divisé par la distance d’observation, le pixel plan étant pratiquement assimilable à la section sphérique (de la sphère centrée sur l’œil d’observation et de rayon égal à la distance d’observation du centre de ce pixel, par le plan de l’écran observé).
À 32 dpi, l’image est perçue comme optimum à 2,4 mètres, au delà l’image parait plus petite. À 40 dpi, l’image est perçue comme non parfaite à une distance inférieure à 1,9 mètres car l’on perçoit les pixels.
Calcul de la résolution d’écran en fonction de la définition
Pour calculer la résolution moyenne d’un écran (en pixels par pouce, souvent abrégé dpi de l’anglais dots per inch, ou bien parfois « ppp »), en tenant compte de sa définition native x × y (en pixels) et de la longueur d de sa diagonale (en pouces), on doit d’abord calculer séparément les résolutions horizontale et verticale de l’écran :
en ayant d’abord converti la diagonale en largeur l et hauteur h (en pouces également) selon
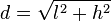
La plupart des modes d’affichage graphique pour moniteurs informatiques génèrent une image avec la même résolution relative horizontalement et verticalement (note : ces résolutions sont relatives car ces images n’ont pas en elles-mêmes de taille physique), mais ce n'est pas le cas de tous les modes, ni non plus des standards de codage utilisés en télévision analogique (SD TV ou ED TV) : par exemple, le mode standard CGA pour moniteur informatique a une définition de 320×200 pixels, mais la résolution verticale relative de l’image est plus faible que la résolution horizontale relative, avec des pixels normalement rendus de façon rectangulaire et plus hauts de 20% que leur largeur relative, et qui nécessitent donc soit une interpolation pour adapter l’image à la résolution de l’écran, soit l'affichage de bandes noires en haut et en bas de l’écran d’un moniteur classique au format 4:3 (ce qui provoque alors un rendu incorrect dans un ratio 16:10).
De plus, les écrans de télévision à tube cathodique ont des résolutions horizontales et verticales différentes liées à la géométrie de leur pixels (y compris les écrans de type Trinitron à maillage rectangulaire).
En revanche, la majorité des dalles graphiques LCD, TFT, LED ou à plasma, utilisés comme moniteurs ou pour la télévision HD utilisent des pixels carrés et donc leurs résolutions horizontale et verticale sont égales à leur résolution moyenne (qui est aussi indépendante de leur définition propre à chaque écran, laquelle est aussi indépendante du mode d’affichage et donc du rapport d’aspect de l’image ou de son facteur d’agrandissement). L’affichage sur ces écrans des émissions analogiques (soit au format PAL/SECAM, soit au format NTSC, les deux catégories ayant des rapports d’aspect différents pour l’image qu’ils génèrent, alors que ces mêmes images sont destinées à des écrans de même ratio classique 3:2) et des émissions numériques SD en format classique 3:2 nécessitent donc aussi soit une interpolation de l’image pour adapter sa définition relative à la définition physique de l’écran (ce qui modifie le rapport d’aspect de l’image), soit l’affichage de bandes noires latérales ou un agrandissement tronquant le haut et le bas de l’image pour adapter la résolution non isotrope de l‘image à la résolution isotrope des moniteurs et écrans de télévisions numériques (afin de préserver le rapport d’aspect de l’image).
Puis on peut calculer la moyenne quadratique des deux résolutions horizontale et verticale de l’écran pour obtenir la résolution moyenne de l’écran (en pixels par pouce), qui exprime en fait la racine carrée d’une densité de pixels par unité de surface :
Des calculs plus complexes peuvent être nécessaires pour des géométries non rectangulaires de pixels (par exemple sur de nombreux écrans cathodiques, le masque n’est pas un maillage rectangulaire, mais un maillage triangulaire, et la résolution verticale doit être calculée en prenant une maille multiple plus grande hexagonale où les pixels visibles sont disposés en bandes alternées disposées horizontalement en quinquonce, et on en déduit la résolution verticale moyenne).
Moniteur classique au format 4:3
Pour un moniteur au format classique 4:3, on a
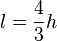
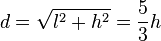
-
Résolution en dpi selon la taille d’écran au format 4:3 Définition
en pixelsTaille de la diagonale en pouces 14 15 17 19 20 21 22 24 26 27 30 32 37 41 46 55 61 69 320 × 240 (QVGA) 28,6 26,7 23,5 21,1 20,0 19,0 18,2 16,7 15,4 14,8 13,3 12,5 10,8 9,8 8,7 7,3 6,6 5,8 400 × 300 35,7 33,3 29,4 26,3 25,0 23,8 22,7 20,8 19,2 18,5 16,7 15,6 13,5 12,2 10,9 9,1 8,2 7,2 480 × 360 42,9 40,0 35,3 31,6 30,0 28,6 27,3 25,0 23,1 22,2 20,0 18,8 16,2 14,6 13,0 10,9 9,8 8,7 640 × 480 (VGA) 57,1 53,3 47,1 42,1 40,0 38,1 36,4 33,3 30,8 29,6 26,7 25,0 21,6 19,5 17,4 14,5 13,1 11,6 768 × 576 (PAL) 68,6 64,0 56,5 50,5 48,0 45,7 43,6 40,0 36,9 35,6 32,0 30,0 25,9 23,4 20,9 17,5 15,7 13,9 800 × 600 (SVGA) 71,4 66,7 58,8 52,6 50,0 47,6 45,5 41,7 38,5 37,0 33,3 31,3 27,0 24,4 21,7 18,2 16,4 14,5 960 × 720 85,7 80,0 70,6 63,2 60,0 57,1 54,5 50,0 46,2 44,4 40,0 37,5 32,4 29,3 26,1 21,8 19,7 17,4 1 024 × 768 (XGA) 91,4 85,3 75,3 67,4 64,0 61,0 58,2 53,3 49,2 47,4 42,7 40,0 34,6 31,2 27,8 23,3 21,0 18,6 1 200 × 900 107,1 100,0 88,2 78,9 75,0 71,4 68,2 62,5 57,7 55,6 50,0 46,9 40,5 36,6 32,6 27,3 24,6 21,7 1 280 × 960 114,3 106,7 94,1 84,2 80,0 76,2 72,7 66,7 61,5 59,3 53,3 50,0 43,2 39,0 34,8 29,1 26,2 23,2 1 400 × 1 050 (SXGA) 125,0 116,7 102,9 92,1 87,5 83,3 79,5 72,9 67,3 64,8 58,3 54,7 47,3 42,7 38,0 31,8 28,7 25,4 1 600 × 1 200 (UXGA) 142,9 133,3 117,6 105,3 100,0 95,2 90,9 83,3 76,9 74,1 66,7 62,5 54,1 48,8 43,5 36,4 32,8 29,0 1 920 × 1 440 171,4 160,0 141,2 126,3 120,0 114,3 109,1 100,0 92,3 88,9 80,0 75,0 64,9 58,5 52,2 43,6 39,3 34,8 2 048 × 1 536 (QXGA) 182,9 170,7 150,6 134,7 128,0 121,9 116,4 106,7 98,5 94,8 85,3 80,0 69,2 62,4 55,7 46,5 42,0 37,1 2 276 × 1 707 203,2 189,7 167,4 149,7 142,3 135,5 129,3 118,5 109,4 105,4 94,8 88,9 76,9 69,4 61,8 51,7 46,6 41,2 2 560 × 1 920 228,6 213,3 188,2 168,4 160,0 152,4 145,5 133,3 123,1 118,5 106,7 100,0 86,5 78,0 69,6 58,2 52,5 46,4
Écran de télévision standard au format 3:2
Pour un écran de télévision au format classique 3:2, on a
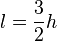
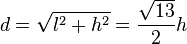
-
Résolution en dpi selon la taille d’écran au format 3:2 Définition
en pixelsTaille de la diagonale en pouces 14 15 17 19 20 21 22 24 26 27 30 32 37 41 46 55 61 69 300 × 200 25,8 24,0 21,2 19,0 18,0 17,2 16,4 15,0 13,9 13,4 12,0 11,3 9,7 8,8 7,8 6,6 5,9 5,2 360 × 240 30,9 28,8 25,5 22,8 21,6 20,6 19,7 18,0 16,6 16,0 14,4 13,5 11,7 10,6 9,4 7,9 7,1 6,3 450 × 300 38,6 36,1 31,8 28,5 27,0 25,8 24,6 22,5 20,8 20,0 18,0 16,9 14,6 13,2 11,8 9,8 8,9 7,8 540 × 360 46,4 43,3 38,2 34,2 32,4 30,9 29,5 27,0 25,0 24,0 21,6 20,3 17,5 15,8 14,1 11,8 10,6 9,4 600 × 400 51,5 48,1 42,4 38,0 36,1 34,3 32,8 30,0 27,7 26,7 24,0 22,5 19,5 17,6 15,7 13,1 11,8 10,5 720 × 480 61,8 57,7 50,9 45,5 43,3 41,2 39,3 36,1 33,3 32,0 28,8 27,0 23,4 21,1 18,8 15,7 14,2 12,5 864 × 576 74,2 69,2 61,1 54,7 51,9 49,4 47,2 43,3 39,9 38,5 34,6 32,4 28,1 25,3 22,6 18,9 17,0 15,0 900 × 600 77,3 72,1 63,6 56,9 54,1 51,5 49,2 45,1 41,6 40,1 36,1 33,8 29,2 26,4 23,5 19,7 17,7 15,7 1 080 × 720 92,7 86,5 76,4 68,3 64,9 61,8 59,0 54,1 49,9 48,1 43,3 40,6 35,1 31,7 28,2 23,6 21,3 18,8 1 152 × 768 98,9 92,3 81,4 72,9 69,2 65,9 62,9 57,7 53,3 51,3 46,2 43,3 37,4 33,8 30,1 25,2 22,7 20,1 1 281 × 854 110,0 102,6 90,6 81,0 77,0 73,3 70,0 64,1 59,2 57,0 51,3 48,1 41,6 37,6 33,5 28,0 25,2 22,3 1 350 × 900 115,9 108,2 95,4 85,4 81,1 77,3 73,7 67,6 62,4 60,1 54,1 50,7 43,9 39,6 35,3 29,5 26,6 23,5 1 440 × 960 123,6 115,4 101,8 91,1 86,5 82,4 78,7 72,1 66,6 64,1 57,7 54,1 46,8 42,2 37,6 31,5 28,4 25,1 1 575 × 1 050 135,2 126,2 111,3 99,6 94,6 90,1 86,0 78,9 72,8 70,1 63,1 59,2 51,2 46,2 41,2 34,4 31,0 27,4 1 800 × 1 200 154,5 144,2 127,3 113,9 108,2 103,0 98,3 90,1 83,2 80,1 72,1 67,6 58,5 52,8 47,0 39,3 35,5 31,4 2 160 × 1 440 185,4 173,1 152,7 136,6 129,8 123,6 118,0 108,2 99,8 96,1 86,5 81,1 70,2 63,3 56,4 47,2 42,6 37,6 2 304 × 1 536 197,8 184,6 162,9 145,7 138,5 131,9 125,9 115,4 106,5 102,6 92,3 86,5 74,8 67,5 60,2 50,3 45,4 40,1 2 400 × 1 600 206,0 192,3 169,7 151,8 144,2 137,4 131,1 120,2 110,9 106,8 96,1 90,1 78,0 70,4 62,7 52,4 47,3 41,8 2 561 × 1 707 219,8 205,2 181,0 162,0 153,9 146,5 139,9 128,2 118,4 114,0 102,6 96,2 83,2 75,1 66,9 56,0 50,4 44,6 2 880 × 1 920 247,2 230,8 203,6 182,2 173,1 164,8 157,3 144,2 133,1 128,2 115,4 108,2 93,5 84,4 75,2 62,9 56,7 50,2
Moniteur large au format 16:10 (ou 8:5)
Pour un moniteur au format large 16:10 (ou 8:5), on a
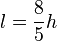
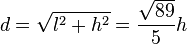
-
Résolution en dpi selon la taille d’écran au format 16:10 (ou 8:5) Définition
en pixelsTaille de la diagonale en pouces 14 15 17 19 20 21 22 24 26 27 30 32 37 41 46 55 61 69 320 × 200 27,0 25,2 22,2 19,9 18,9 18,0 17,2 15,7 14,5 14,0 12,6 11,8 10,2 9,2 8,2 6,9 6,2 5,5 384 × 240 32,3 30,2 26,6 23,8 22,6 21,6 20,6 18,9 17,4 16,8 15,1 14,2 12,2 11,0 9,8 8,2 7,4 6,6 480 × 300 40,4 37,7 33,3 29,8 28,3 27,0 25,7 23,6 21,8 21,0 18,9 17,7 15,3 13,8 12,3 10,3 9,3 8,2 576 × 360 48,5 45,3 40,0 35,7 34,0 32,3 30,9 28,3 26,1 25,2 22,6 21,2 18,4 16,6 14,8 12,3 11,1 9,8 640 × 400 53,9 50,3 44,4 39,7 37,7 35,9 34,3 31,4 29,0 28,0 25,2 23,6 20,4 18,4 16,4 13,7 12,4 10,9 768 × 480 64,7 60,4 53,3 47,7 45,3 43,1 41,2 37,7 34,8 33,5 30,2 28,3 24,5 22,1 19,7 16,5 14,8 13,1 960 × 600 80,9 75,5 66,6 59,6 56,6 53,9 51,5 47,2 43,5 41,9 37,7 35,4 30,6 27,6 24,6 20,6 18,6 16,4 1 152 × 720 97,0 90,6 79,9 71,5 67,9 64,7 61,7 56,6 52,2 50,3 45,3 42,5 36,7 33,1 29,5 24,7 22,3 19,7 1 440 × 900 121,3 113,2 99,9 89,4 84,9 80,9 77,2 70,8 65,3 62,9 56,6 53,1 45,9 41,4 36,9 30,9 27,8 24,6 1 536 × 960 129,4 120,8 106,5 95,3 90,6 86,3 82,3 75,5 69,7 67,1 60,4 56,6 49,0 44,2 39,4 32,9 29,7 26,3 1 680 × 1 050 141,5 132,1 116,5 104,3 99,1 94,3 90,1 82,5 76,2 73,4 66,0 61,9 53,5 48,3 43,1 36,0 32,5 28,7 1 920 × 1 200 161,7 150,9 133,2 119,2 113,2 107,8 102,9 94,3 87,1 83,9 75,5 70,8 61,2 55,2 49,2 41,2 37,1 32,8 2 304 × 1 440 194,1 181,1 159,8 143,0 135,8 129,4 123,5 113,2 104,5 100,6 90,6 84,9 73,4 66,3 59,1 49,4 44,5 39,4 2 560 × 1 600 215,6 201,3 177,6 158,9 150,9 143,8 137,2 125,8 116,1 111,8 100,6 94,3 81,6 73,6 65,6 54,9 49,5 43,8 3 072 × 1 920 258,8 241,5 213,1 190,7 181,1 172,5 164,7 150,9 139,3 134,2 120,8 113,2 97,9 88,4 78,8 65,9 59,4 52,5
Écran de télévision large au format 16:9
Pour un écran de télévision au format large 16:9, on a
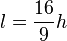
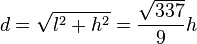
-
Résolution en dpi selon la taille d’écran au format 16:9 Définition
en pixelsTaille de la diagonale en pouces 14 15 17 19 20 21 22 24 26 27 30 32 37 41 46 55 61 69 640 × 360 52,5 49,0 43,2 38,6 36,7 35,0 33,4 30,6 28,2 27,2 24,5 22,9 19,8 17,9 16,0 13,4 12,0 10,6 1 024 × 576 83,9 78,3 69,1 61,8 58,7 55,9 53,4 49,0 45,2 43,5 39,2 36,7 31,8 28,7 25,5 21,4 19,3 17,0 1 280 × 720 104,9 97,9 86,4 77,3 73,4 69,9 66,8 61,2 56,5 54,4 49,0 45,9 39,7 35,8 31,9 26,7 24,1 21,3 1 600 × 900 131,1 122,4 108,0 96,6 91,8 87,4 83,4 76,5 70,6 68,0 61,2 57,4 49,6 44,8 39,9 33,4 30,1 26,6 1 920 × 1 080 157,4 146,9 129,6 115,9 110,1 104,9 100,1 91,8 84,7 81,6 73,4 68,8 59,5 53,7 47,9 40,1 36,1 31,9 2 560 × 1 440 209,8 195,8 172,8 154,6 146,9 139,9 133,5 122,4 113,0 108,8 97,9 91,8 79,4 71,6 63,9 53,4 48,2 42,6
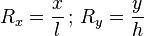
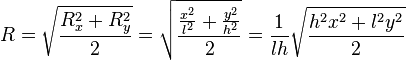
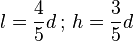
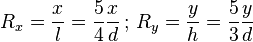
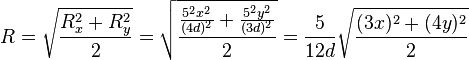
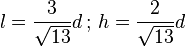
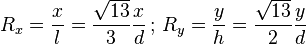
![R=\sqrt{\frac{R_x^2+R_y^2}{2}}=\sqrt{\frac{\frac{13x^2}{(3d)^2}+\frac{13y^2}{(2d)^2}}{2}}=\frac{1}{6d}\sqrt{\frac{13[(2x)^2+(3y)^2]}{2}}](https://static.techno-science.net/illustration/Definitions/autres/1/16c797affb5d08133c15b6ea6da469aa_9c457f33be29a2e826253348f50d06a1.png)
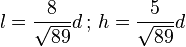
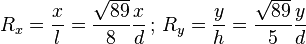
![R=\sqrt{\frac{R_x^2+R_y^2}{2}}=\sqrt{\frac{\frac{89^2}{(8d)^2}+\frac{89y^2}{(5d)^2}}{2}}=\frac{1}{40d}\sqrt{\frac{89[(8x)^2+(5y)^2]}{2}}](https://static.techno-science.net/illustration/Definitions/autres/1/10d8244dad8063afdcf3df2396d0bfbe_d6262cca31211a73693ff9dafdb4b37b.png)
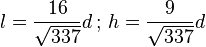
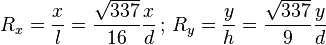
![R=\sqrt{\frac{R_x^2+R_y^2}{2}}=\sqrt{\frac{\frac{337x^2}{(16d)^2}+\frac{337y^2}{(9d)^2}}{2}}=\frac{1}{144d}\sqrt{\frac{337[(9x)^2+(16y)^2]}{2}}](https://static.techno-science.net/illustration/Definitions/autres/6/6f93685470fc053be8c2bdc3fbb0f8b8_8c3f4746ac03d6e842ceedb95a3d6fa5.png)

















































