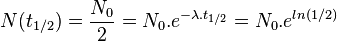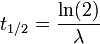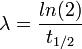Décroissance radioactive - Définition

Période radioactive

On appelle « période radioactive » (ou demi-vie) T_1/2 la durée au bout de laquelle le nombre de radionucléides présents dans l'échantillon est réduit de moitié. Si N(t) représente le nombre de radionucléide à un instant t, alors :

On en déduit immédiatement :

ou encore:

Où N₀ est le nombre de noyaux initiaux, et λ est la constante radioactive correspondant au type de noyaux.

Vie moyenne

Il ne faut pas confondre la demi-vie avec la vie moyenne t. Celle-ci s'obtient par le raisonnement suivant : La quantité de noyaux qui se désintègrent à l'instant t a « vécu » pendant cette durée t ou, plus exactement, à l'instant t il reste N₀ exp(–λ t) noyaux présents. De ceux-ci, pendant une durée dt, il s'en détruit

dN = λ N₀ exp(–λ t) dt.

Ces dN ont donc une durée de vie comprise entre t et t + dt. On peut donc définir la durée moyenne de vie pour l'ensemble des radionucléides de l'échantillon (ou simplement vie moyenne) par

t = ∫_N0→0 t dN / N₀.

En tenant compte de l'expression de dN donnée ci-dessus, on obtient donc

t = λ ∫_0→∞ t exp(–λ t) dt = λ^–1 ≅ 2,718 T_1/2.

Dans la littérature scientifique, on désigne généralement la durée de vie radioactive moyenne par la lettre grecque τ, donc

τ = t = λ^–1. Cette durée de vie ne dépend pas de la taille de l'échantillon N₀ ; c'est un temps caractéristique du radionucléide considéré, tout comme sa période T_1/2. Au bout de ce temps caractéristique τ, l'activité est réduite à la fraction 1/e de sa valeur initiale :

N(τ) = N₀ exp(–λ/λ) = N₀/e.

Filiation de deux isotopes dépendants

• Cas général

Soit l'isotope 1 qui se transforme en isotope 2 selon une constante radioactive λ₁. L'isotope 2 décroît selon la constante radioactive λ₂.

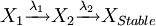
La décroissance de l'isotope 1 n'est pas influencée par l'isotope 2. Par contre, la quantité d'isotope 2 au temps t dépend de la quantité d'isotope 1 à l'origine et des deux constantes radioactives λ₁ et λ₂.

On a donc : dN₁ = − λ₁N₁dt et dN₂ = λ₁N₁dt − λ₂N₂dt

Ainsi, pour atteindre un éventuel équilibre entre les activités des deux isotopes, il faut une durée :

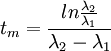
• La période de l'isotope 1 est inférieure à la période de l'isotope 2

Quand t > > 10T₁, alors
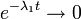
Au bout d'une durée équivalente à au moins 10 fois la période de l'isotope 1, la décroissance de l'isotope 2 ne dépend plus de l'isotope 1.

• La période de l'isotope 1 est supérieure à la période de l'isotope 2

Au bout d'un certain temps, un équilibre de régime est obtenu, tel que :

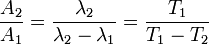
• La période de l'isotope 1 est très supérieure à la période de l'isotope 2

Un équilibre séculaire est observé au bout d'environ 10 fois la période de l'isotope 2.
Les activités des deux isotopes sont alors équivalentes et décroissent selon la constante radioactive de l'isotope 1.

Exemple : Décroissance du plutonium 240

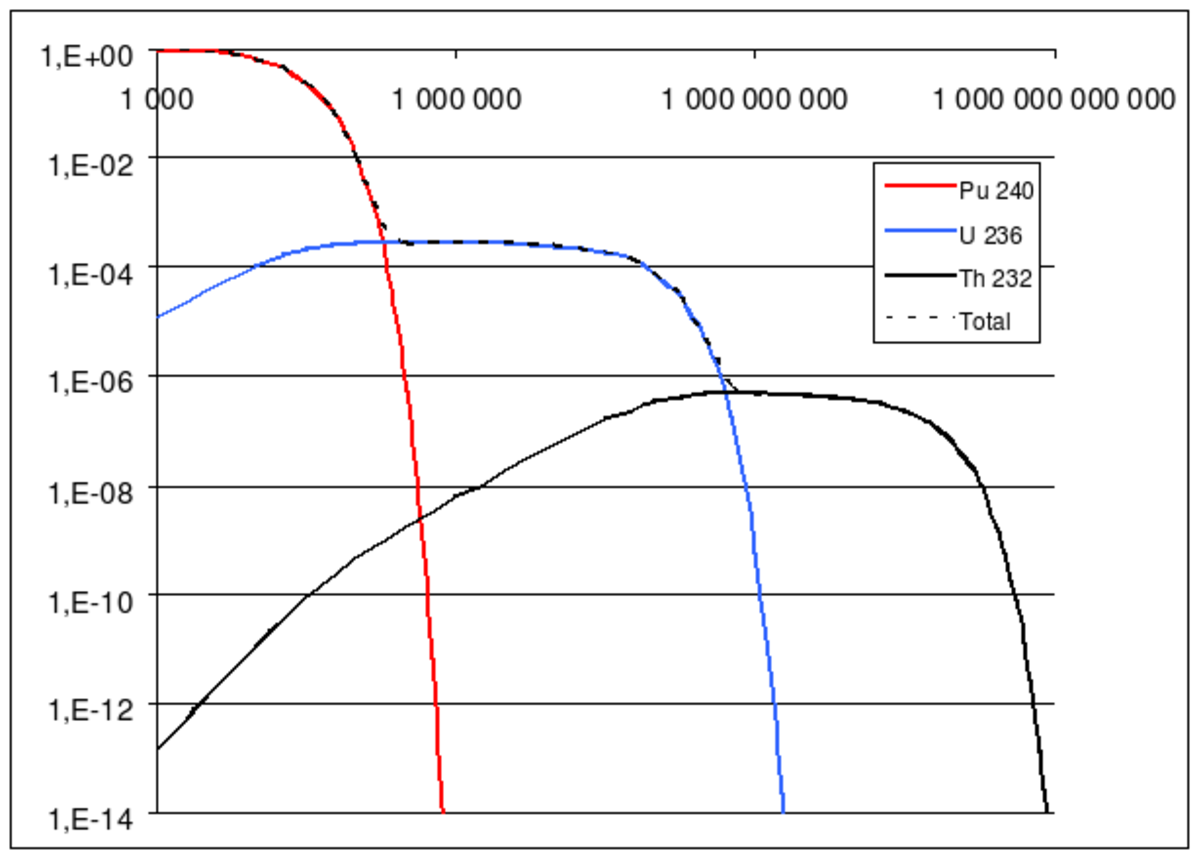
Le Plutonium 240 (période 6560 ans) se désintègre en Uranium 236 (23,42×10^6 ans), lequel se désintègre à son tour en Thorium 232 pratiquement stable (14,05×10^9 ans). Quand on représente la radioactivité de ces trois corps en fonction du temps, sur un diagramme log/log, on distingue bien trois zones distinctes:

• Le temps du plutonium: Tant que l'on ne dépasse pas la demi-vie du plutonium 240, la radioactivité du plutonium reste sensiblement constante. Pendant ce temps, la radioactivité de l'uranium 236 croît linéairement en fonction du temps (la pente de la courbe est de 1), et le thorium 232 croît comme le carré du temps (la pente de la courbe est de 2). Quand on arrive autour de la demi-vie du plutonium (entre 10 000 et 100 000 ans), son taux de radioactivité baisse significativement, et devient inférieur à celui de l'Uranium 236.
• Le temps de l'uranium: entre la demi-vie du plutonium et celle de l'uranium, la radioactivité reste sensiblement constante, mais c'est celle de l'uranium qui domine à présent. Pendant ce temps, la radioactivité du plutonium 240 perd plusieurs ordres de grandeurs, et devient globalement négligeable devant le reste. La radioactivité du thorium 232 continue à croître, mais sa croissance n'est à présent que linéaire (parce que la quantité d'uranium n'augmente plus). Quand on atteint la demi-vie de l'uranium 236 (100 à 1000 millions d'années), le taux de radioactivité de l'uranium 236 devient inférieur à celui du Thorium 232.
• Le temps du Thorium : après un milliard d'années, c'est la radioactivité du thorium qui est dominante, et celle de ses précurseurs devient négligeable. Le Thorium devient lui-même négligeable après sa demi-vie, soit de l'ordre de mille milliards d'années.

Par rapport à l'univers, nous sommes actuellement à l'âge du thorium. La terre s'est formée il y a un peu plus de quatre milliards d'années, et le Big Bang ne date « que » de 13 milliards d'années: Le plutonium et l'uranium qui avaient pu se former dans les étoiles de première génération ont disparu depuis longtemps, mais le thorium originel subsiste encore en quantités appréciables.

Filiations de n isotopes dépendants

• Soit une filiation de n isotopes :

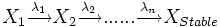
L'activité du ennième isotope peut être calculé d'après les équations de Bateman et à partir de la quantité d'isotope 1 au départ (N1)

Dans le cas particulier où le premier isotope aurait une période (T1) très longue par rapport à celles des isotopes-fils, au bout de dix fois (T1), un équilibre séculaire s'installe et tous les isotopes ont la même activité. A₁ = A₂ = A₃ = ... = A_n
cet équilibre n'est réalisé que si les différents isotopes de la chaine restent piégés.

• Exemple

Un exemple particulier est celui des trois chaines radioactives présentes naturellement dans l'écorce terrestre et dont les isotopes pères sont : l'uranium 238, le thorium 232 et l'uranium 235.