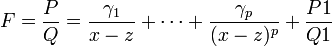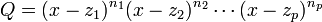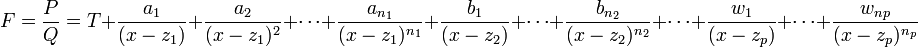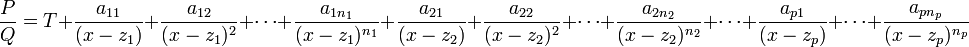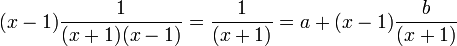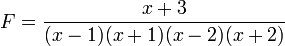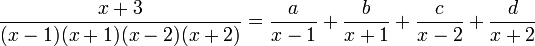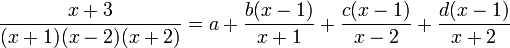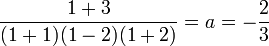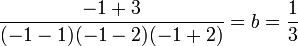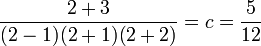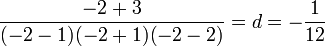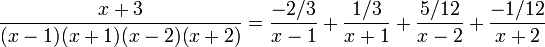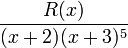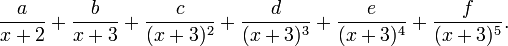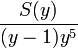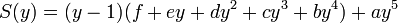Décomposition en éléments simples - Définition
La liste des auteurs de cet article est disponible ici.
Décomposition en éléments simples dans les complexes
Principes généraux
On dit que z est un pôle d’ordre p de la fraction irréductible
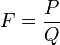
Théorème — Si z est pôle d’ordre p de
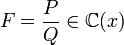
où la fraction rationnelle
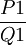
Or d'après le théorème fondamental de l'algèbre, le polynôme Q possède, dans
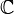
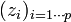
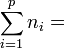
La propriété précédente se généralise alors à
Théorème — Soit
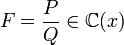
alors F admet la décomposition unique en éléments simples suivante
où les
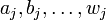
Note : Pour des raisons de simplicité d'écriture on peut aussi noter
où les aij sont des nombres complexes.
Exemples de décompositions
L'existence d'une décomposition étant établie, la difficulté réside dans la détermination des différents coefficients. Certaines techniques sont applicables dans le corps des complexes ou dans le corps des réels dès que le polynôme Q est produit de facteurs du premier degré. Dans un souci de lisibilité, les exemples sont ici donnés avec des coefficients réels.
Cas où tous les pôles sont simples
Étude d'un exemple avec deux pôles simples :
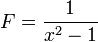
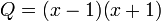
On en déduit que F peut s'écrire sous la forme :
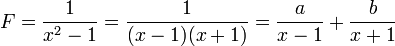
Il s'agit de déterminer a et b. Une méthode qui est toujours réalisable consiste à réduire au même dénominateur le membre de droite de la décomposition et à identifier les coefficients des numérateurs. Cette méthode n'est pas très efficace car elle demande la résolution d’un nombre d’équations correspondant au nombre de coefficients à déterminer. On peut réduire grandement le travail en éliminant, par une multiplication judicieuse, tous les coefficients sauf un. Ainsi dans notre exemple en multipliant par (x-1), on obtient
En posant alors x= 1, il vient a= 1/2
Puis, en multipliant F par (x+1) et en posant x= -1, il vient b= -1/2 puisque
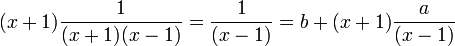
La fraction F se décompose alors en
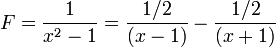
Exemple avec quatre pôles simples :
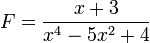
qui se décompose en
Pour trouver le coefficient a, il suffit de multiplier les deux membres par x - 1 puis de remplacer x par 1
De même pour trouver b, il suffit de multiplier par x + 1 et de remplacer x par -1
Pour c, il suffit de multiplier par x - 2 et de remplacer x par 2
et pour d, on multiplie par x + 2 et on remplace x par -2
Donc
Cas où certains pôles sont multiples
Pour une fraction rationnelle de la forme
(où R(x) est un polynôme quelconque de degré strictement inférieur à 6), -2 est un pôle simple (i.e. d'ordre 1) mais -3 est un pôle multiple (d'ordre 5>1). La décomposition en fractions partielles aura comme allure
La détermination des coefficients a, b, c, d, e, f s'opère en effectuant le changement de variable y = x + 3 (autre méthode que précédemment mais qui conduit au même résultat final). La fraction s'écrit alors
La division de S(y) par y - 1 suivant les puissances croissantes (voir Division d'un polynôme) nous donne alors
Il suffit alors d'opérer la division et de revenir à la variable de départ.