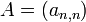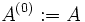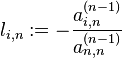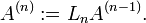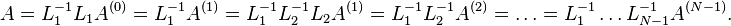Décomposition LU - Définition

Calcul de la décomposition

Idée principale

La décomposition LU est une forme particulière d'élimination de Gauss Jordan. On transforme la matrice A en une matrice triangulaire supérieure U en éliminant les éléments sous la diagonale. Les éliminations se font colonne après colonne, en commençant par la gauche, en multipliant A par la gauche avec une matrice triangulaire inférieure.

Algorithme

Étant donné une matrice de dimension

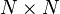
on définit

et les itérations se font pour n = 1,...,N-1 de la manière suivante.

Sur nième colonne de A^(n-1), on élimine les éléments sous la diagonale en ajoutant à la ième ligne de cette matrice, la nième ligne multipliée par

pour . Ceci peut être fait en multipliant par la gauche A^(n-1) avec la matrice triangulaire inférieure

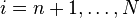
Après N-1 itérations, nous avons éliminé tous les éléments sous la diagonale, par conséquent, nous avons maintenant une matrice triangulaire supérieure A^(N-1).

Nous obtenons la décomposition

Notons U la matrice triangulaire supérieure A^(N-1) et . Sachant que l'inverse d'une matrice triangulaire inférieure est aussi une matrice triangulaire inférieure et que le produit de 2 matrices triangulaires inférieures est encore une matrice triangulaire inférieure, L est donc une matrice triangulaire inférieure. On obtient A = LU.

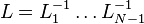
Au vu de l'algorithme, il est nécessaire que à chaque itération (voir la définition de l_i,n). Si, au cours du calcul, ce cas de figure venait à se produire, il faut intervertir la nième ligne avec une autre pour pouvoir continuer (il est toujours possible de trouver un élément non nul sur la colonne qui pose problème car la matrice est inversible). C'est la raison pour laquelle la décomposition LU s'écrit généralement P ^{− 1}A = LU.

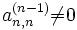
Le cas symétrique

• Si la matrice A est une matrice symétrique, il existe une décomposition dite factorisation de Crout

A = L.D.^tL

où L est une matrice triangulaire inférieure dont la diagonale ne comprend que des 1, ^tL est la transposée de L, et D est une matrice diagonale.

• Si la matrice A est symétrique définie positive, il existe une décomposition plus simple, donnée par la méthode de Cholesky

A = L.^tL

où L est une matrice triangulaire inférieure à diagonale positive et ^tL est la transposée de L.

Existence, unicité

Pour toute matrice carrée, on a existence d'une décomposition PLU. La décomposition LU existe si et seulement si toutes les sous matrices principales d'ordre 1 à n-1 sont inversibles. Si toutes les sous matrices principales d'ordre 1 à n sont inversibles, elle est unique.