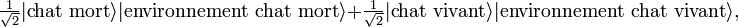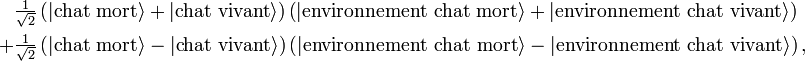Décohérence quantique - Définition
La liste des auteurs de cet article est disponible ici.
Les problèmes de transition quantique/classique
Le problème majeur est que la physique quantique admet des états superposés, ces états étant absolument inconnus à un niveau macroscopique, décrit par la physique classique. L'exemple le plus frappant décrivant ce problème est l'expérience du chat de Schrödinger. Dans cette expérience de pensée, l'état superposé d'une particule (désintégrée/non désintégrée) doit se propager, en suivant scrupuleusement les règles quantiques, à l'état d'un chat qui devrait également être, selon ces règles, dans un état superposé mort/vivant. Or, un tel état n'est jamais observé, d'où paradoxe et problème.
La théorie quantique tient compte de cette non-observabilité des états superposés quantiques en stipulant que tout acte d'observation provoque un effondrement de la fonction d'onde, c'est-à-dire sélectionne instantanément un et un seul état parmi l'ensemble des états superposés possibles. Cela donne lieu à un postulat spécifique (postulat 5 dit de « Réduction du paquet d'onde »), qui est en contradiction mathématique avec un autre postulat de la mécanique quantique (postulat 6 : l'équation de Schrödinger). Voir « Problème de la mesure quantique » pour une présentation détaillée de ce problème.
Tel est le problème principalement traité par la théorie de la décohérence. D'autres problèmes interviennent dans la transition quantique ⇒ classique, comme le problème du déterminisme, ou des paradoxes de non-localité, mais qui ne sont pas spécifiquement traités par cette théorie.
Décohérence et Réduction du paquet d'onde
On voit d'après ce qui précède qu'il ne faut pas confondre décohérence et réduction du paquet d'onde. Voici un tableau récapitulant les différences :
| Réduction du paquet d'onde | Décohérence |
|---|---|
| Postulat indépendant | Déduit d'un postulat |
| Durée de la réduction instantanée | Durée dépendante de l'environnement |
| Les états superposés n'existent plus après la réduction | États superposés indétectables |
| Réduction provoquée par un acte de mesure, de nature subjective | Réduction spontanée, objective |
| Universalité postulée | Universalité vraisemblable |
| Sélectionne un état unique | Sélectionne un ensemble d'états mutuellement exclusifs |
Il n'est pas encore tranché de savoir si la décohérence est une approximation du postulat de réduction du paquet d'onde, ou si c'est au contraire le postulat qui approxime la réalité de la décohérence. Malgré tout, nombreux sont les physiciens penchant vers la deuxième hypothèse.
État des lieux de la théorie de la décohérence
Aujourd'hui, cette théorie est considérée comme étant l'approche la plus aboutie pour résoudre le problème de la mesure quantique. Elle a reçu un grand nombre de confirmations expérimentales.
Toutefois des problèmes subsistent, qui ne sont pas entièrement, ou pas du tout, résolus par cette théorie.
États superposés de probabilité non nulle
Dans la théorie de la décohérence, l'état est décrit dans le formalisme de la matrice densité, la base de mesure étant sélectionnée par l'environnement selon un processus nommé einselection (pour environment induced selection ) par Zurek. Dans cette base, les éléments non diagonaux de la matrice densité, également appelés cohérences, tendent exponentiellement vers zéro avec un temps caractéristique très court, mais ne deviennent jamais rigoureusement nuls. Cela est d'ailleurs théoriquement impossible, car les lois quantiques sont invariantes par changement de base de l'espace de Hilbert représentant les états quantiques, alors qu'une diagonalisation parfaite n'est valable que dans une base donnée. Ceci est en contradiction avec le postulat de réduction du paquet d'onde, qui stipule que les états superposés disparaissent rigoureusement. La théorie de la décohérence arrive donc à déduire ce postulat, mais que de manière approchée.
Toutefois, les coefficients sont tellement faibles que toute mise en évidence des états superposés résiduels est absolument impossible en pratique, même si l'expérience utilise toute la matière et l'énergie de l'univers et ce, même pour des interactions relativement faibles. Cela permet donc d'affirmer que la décohérence est en pratique similaire sur ce point au postulat de réduction du paquet d'onde.
Unicité de la mesure
La décohérence mène non pas à un état unique, comme dans la réalité, mais à un ensemble d'états mutuellement exclusifs dont les probabilités sont régies par les lois de la physique quantique.
Par exemple, la matrice densité du chat de Schrödinger évolue par décohérence en
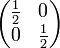
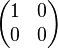
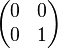
Ainsi, le mécanisme qui "choisit" l'état final du chat échappe à la théorie de la décohérence. Or, le postulat de réduction du paquet d'onde stipule que l'état final est bien projeté sur une et une seule valeur. Ce postulat n'est donc pas entièrement couvert par la théorie de la décohérence.
Les tenants de la théorie de la décohérence opposent à ce constat les considérations suivantes :
- La théorie de la décohérence n'apporte pas d'indications à propos de l'unicité du réel, mais cette unicité est compatible avec la théorie de la décohérence. On n'en demande pas plus à une théorie physique.
- Étant donné que l'état d'un système représente les informations accessibles sur lui, le fait que les différents états soient mutuellement exclusifs suite à une décohérence implique que l'état physique prend bien une et une seule valeur, les autres valeurs étant inaccessibles. Avec cette définition de l'état d'un système, l'unicité découle implicitement de l'exclusion mutuelle qui elle-même est une conséquence de la décohérence. Par transitivité, on peut conclure que l'unicité découle implicitement de la décohérence.
Universalité de la décohérence
La question peut se poser de savoir si le mécanisme de la décohérence s'applique dans tous les cas de figure où s'applique le postulat de réduction du paquet d'onde. Il s'avère que certains cas importants échappent au formalisme de la décohérence, notamment ceux où les observables apparaissent en cours de mesure, comme par exemple dans le cas des chambre à bulles. Il n'y a donc aucune preuve formelle que le mécanisme de la décohérence s'applique à ces cas de figure. Toutefois, il n'y a pas non plus de preuve du contraire, et l'opinion largement répandue est qu'il est vraisemblable que la décohérence soit un phénomène universel.
Interprétation de la matrice densité
La théorie de la décohérence est entièrement fondée sur le formalisme de la matrice densité et n'est pas prouvée en dehors de ce cadre. Certains physiciens, et notamment Roger Penrose, soulignent les problèmes de l'utilisation d'une matrice densité pour extrapoler des propriétés concernant les phénomènes quantiques. Les problèmes sont de deux ordres :
- La matrice densité représente, selon ce point de vue, une approximation du réel car ce formalisme est utilisé quand le détail du système quantique examiné ne peut être connu. Rien ne prouve qu'un phénomène crucial n'a pas été négligé dans l'approximation de la matrice densité (par exemple, la gravitation), ou que des artefacts n'apparaissent pas, dus à cette approximation.
- Et surtout, une même matrice densité peut avoir un grand nombre d'interprétations "réelles". Quand la théorie de la décohérence prouve que la matrice densité se diagonalise, il reste à montrer pourquoi et par quel mécanisme la nature choisit une interprétation de cette matrice plutôt qu'une autre.
Ainsi, la même matrice densité
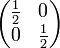
qui est la solution du paradoxe du Chat de Schrödinger selon la théorie de la décohérence, que :
qui est un état physique tout à fait légal et possible selon les règles quantiques (on arrive d'ailleurs à superposer réellement de cette manière des paires de particules EPR).
Il reste à démontrer, dans la théorie de la décohérence, pourquoi seule la première possibilité advient dans la réalité et jamais la seconde, alors que les deux formes sont parfaitement légales selon la théorie quantique.