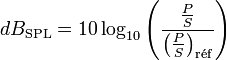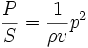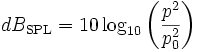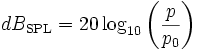Décibel - Définition

Unité acoustique

dBSPL

Le décibel, de symbole dB, est une unité relative de l’intensité acoustique. Le dBSPL (Sound Pressure Level) est défini par le rapport de la puissance par unité de surface du son que l’on mesure et une puissance par unité de surface de référence :

La puissance par unité de surface de référence est 10^-12 W·m^-2 (un picowatt par mètre carré).

La puissance par unité de surface transportée par une onde sonore est reliée à la pression acoustique par la formule :

où :

• est la puissance par unité de surface ou intensité acoustique(en W·m^-2).
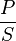
• p est la pression acoustique efficace (en pascal).
• ρ est la masse volumique du milieu (en kg·m^-3).
• v est la vitesse du son dans le milieu (en m·s^-1).

Si, dans la formule de la première définition, on remplace la puissance par unité de surface par la formule en fonction de la pression acoustique, la densité et la vitesse se simplifient et on obtient :

Si on sort le carré du logarithme on obtient la seconde version de la définition de dBSPL :

p est le niveau de pression du son (en valeur efficace) et est la pression de référence que l’on accepte comme le niveau à partir duquel l’oreille humaine commence à percevoir un son pur de 1 kHz. Celui-ci est de 20 µPa (valeur efficace). Les deux valeurs de référence (1 picowatt par mètre carré et 20 µPa efficaces) sont équivalentes pour l’air à la température et pression ambiante.

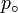
Par ailleurs, pour un même niveau acoustique à différentes fréquences, l’homme ne perçoit pas le même niveau d’intensité. Pour un même niveau d’intensité acoustique de 20 dBSPL, un son pur de 1 kHz paraîtra plus fort qu’un son de 10 kHz tandis qu’un son de 100 Hz ne sera pas perçu. Pour avoir le même niveau perçu, le son de 10 kHz devra être à 30 dBSPL et le son de 100 Hz à 50 dBSPL. Les courbes isosoniques représentent les courbes de même intensité perçue qu’un son pur de 1 kHz à un niveau acoustique donné.

dBHL

Intensité perçue par l’oreille humaine normale.

dBSL

Intensité perçue par un individu donné.

Le seuil de perception auditive

Le niveau de 0 phone ou 0 dB SPL est un niveau vraiment bas. Pour s’en rendre compte, voici à quoi ce niveau de 0 dB SPL correspond :

• en puissance par mètre carré : à 0,5 watts repartis sur toute la surface de la France métropolitaine ;
• en pression : à la pression due au poids d’une couche de 2×10^-9 m d’eau (environ 20 atomes d’épaisseur) ;
• en déplacement des molécules dans l’air : à une oscillation (crête à crête) de 2×10^-11 m, c’est-à-dire deux dixièmes de l’épaisseur d’un atome.

dB pondéré

Il existe plusieurs courbes de pondération : A, B, et C. La courbe de pondération (A) correspond de près à la correction de l’oreille humaine. Moins sensible aux BF (basses fréquences) et plus sensibles aux HF (hautes fréquences). Cependant, ce n’est pas exactement ce que déchiffre notre cerveau. Pour cela, il faut additionner les niveaux sonores pondérés relevés en fonction des fréquences. Attention, 80 dB (A) + 80 dB (A) n’est pas égal à 160 dB(A) mais à 83 dB(A). Plus la différence entre deux sons est élevée moins on majore. Le bruit d’un avion 120 dB (A) + le bruit d’une voiture 80 dB(A) = 120 dB(A). L’avion couvre complètement le bruit de la voiture. Pour bien comprendre Le dB(A) est un niveau sonore global (son perçu par l’oreille) et le dB est un niveau sonore qui n’a de sens que lorsqu’il est noté pour une fréquence donnée.

Pour prendre en compte cette sensibilité de l’oreille par rapport aux fréquences, le dB(A) est utilisé. Une courbe isosonique a été définie correspondant à un niveau perçu de 40 dB pour un son pur de 1 kHz. L’inverse de cette courbe pondère le signal et l’on obtient le niveau en dB(A) par intégration sur toutes les fréquences. Cette unité est très fréquemment utilisée dans les indicateurs acoustiques du bruit.