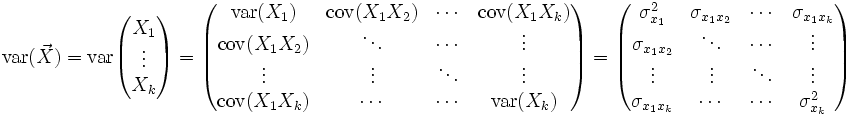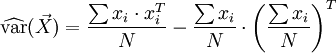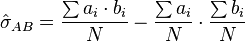Covariance - Définition

Matrice de variance-covariance

Définition

La matrice de variance-covariance (ou simplement matrice de variance) d'un vecteur de k variables aléatoires est la matrice carrée donnée par:

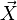
Vu la propriété que , il s'agit d'une matrice symétrique. L'inverse de la matrice de covariance est parfois désignée par le terme de « matrice de précision ». La matrice de covariance est un cas particulier de matrice de Gram.

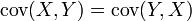
Estimation

Un estimateur de la matrice de variance-covariance de N réalisations d'un vecteur de variables aléatoires peut être donné par:

Estimation

Un estimateur de la covariance de deux variables aléatoires A et B observées conjointement N fois est donné par:

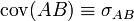
Usage

La connaissance des covariances est le plus souvent indispensable dans les fonctions d'estimation, de filtrage et de lissage. Elles permettent, entre autres en photographie, d'arriver à corriger de façon spectaculaire les flous de mise au point ainsi que les flous de bougé, ce qui est extrêmement important pour les clichés astronomiques. On les utilise également en automatique. En sociolinguistique, la covariance désigne la correspondance entre l’appartenance à une certaine classe sociale et un certain parler inhérent à cette condition sociale.