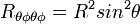Courbure de Gauss - Définition
La liste des auteurs de cet article est disponible ici.
Application à la sphère
Courbure de Gauss de la sphère en coordonnées de Riemann
L’équation d’une sphère de rayon R en coordonnées cartésiennes dans l’espace euclidien à trois dimensions est
- x2 + y2 + z2 = R2.
Pour que la concavité soit positive, on doit prendre la racine négative pour z :
Développons-la en série au pôle Sud, au voisinage de x = y = 0, c’est-à-dire en coordonnées de Riemann :
D'où par différentiation :
La métrique de l’espace euclidien à trois dimensions
devient celle d’un paraboloïde de révolution approximant la sphère :
Plus près du pôle Sud, où x ≈ y ≈ 0, la métrique est euclidienne en éliminant les termes du second ordre. Pour la mettre en coordonnées de Riemann il est nécessaire de la diagonaliser. Il est plus simple d'utiliser les coordonnées sphériques qui donnent une métrique diagonale. Pour être en coordonnées de Riemann, on diagonalise la métrique, qui devient :
où K = kxky est la courbure de Gauss. On retrouve la métrique euclidienne en O où x et y sont nuls. Dans cette expression, on a gxx = 1, gxy = 0 et
On retrouve bien la courbure de Gauss de la sphère, égale au tenseur de Riemann Ruvuv mais uniquement en coordonnées de Riemann.
Courbure de Gauss de la sphère en coordonnées de Gauss
Considérons un petit rectangle élémentaire sur la sphère de rayon R. Soit θ la colatitude et φ la longitude. Sa diagonale ds est, en vertu du théorême de Pythagore:
La métrique de la sphère est diagonale, sans terme rectangle :
La formule générale de la courbure de Gauss en coordonnées de Gauss pour une métrique diagonale :
se simplifie sur la sphère en éliminant les termes nuls :
puis, en explicitant les coefficients de la métrique :
et enfin en :
Le tenseur de Riemann de la sphère est
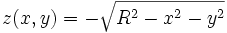
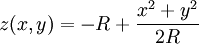
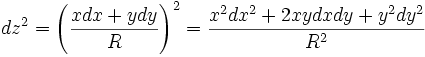
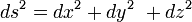
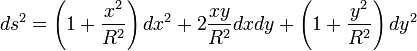
![ds^2= dx^2 + \left[1 - \frac{ x^2 + y^2}{R^2}\right] dy^2](https://static.techno-science.net/illustration/Definitions/autres/a/a9ff6dd4adf330fa6fa219c5311763ca_d8012a317ba4e57ce7c405945d096be9.png)
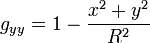
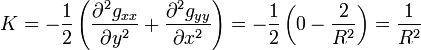
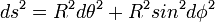
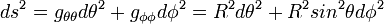
![K= \frac{1}{g_{\theta\theta}g_{\phi\phi}} \left[ -\frac12 \left(g_{\theta\theta,\phi\phi}+g_{\phi\phi,\theta\theta}\right) +\frac{g_{\theta\theta,\phi}^2}{4g_{\theta\theta}}+\frac{g_{\phi\phi,\theta}^2}{4g_{\phi\phi}} +\frac{g_{\theta\theta,\theta}^2g_{\phi\phi,\theta}}{4g_{\theta\theta}}+\frac{g_{\phi\phi,\phi}^2g_{\theta\theta,\phi}}{4g_{\phi\phi}} \right]](https://static.techno-science.net/illustration/Definitions/autres/7/7b021b12e7f205e9c176506f52b8a75e_b25f0368fe2aea155024a0d5f301fa01.png)
![K= \frac{1}{g_{\theta\theta}g_{\phi\phi}} \left[ -\frac12 \left(0+g_{\phi\phi,\theta\theta}\right) +0+\frac{g_{\phi\phi_,\theta}^2}{4g_{\phi\phi}} +0+0 \right]](https://static.techno-science.net/illustration/Definitions/autres/a/a92a9593d9ee8cba60c918a7c95dd6f7_f21a97b0d6e47d29d7027a098c4a1548.png)
![K= \frac{1}{R^4sin^2\theta} \left[ -\frac12 \times 2R^2 (sin\theta cos\theta)_{,\theta} +\frac{4R^4sin^2 \theta cos^2 \theta}{4R^2sin^2\theta} \right]](https://static.techno-science.net/illustration/Definitions/autres/a/a429e5fa33470fc536765e42936e5e1a_d3b7fc84de1d17c07ecec69fd6b153f9.png)
![K= \frac{1}{R^2sin^2\theta} \left[ -\left(cos^2\theta-sin^2\theta \right) +\frac{sin^2 \theta cos^2 \theta}{sin^2\theta} \right]= \frac{1}{R^2}](https://static.techno-science.net/illustration/Definitions/autres/6/66f24e440ea80fc74ba0038f1ab3d73c_831634d8483c885eed1dd7bd7b823c66.png)