Courbe elliptique - Définition
La liste des auteurs de cet article est disponible ici.
Courbes elliptiques sur le corps des nombres complexes
L'équation d'une courbe elliptique sur le corps des complexes peut aussi être mise sous la forme de Weierstrass. Il est d'usage d'adopter ici la normalisation
où g2 et g3 sont des nombres complexes.
Un résultat déterminant est qu'une courbe elliptique définie sur
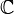
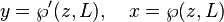
où
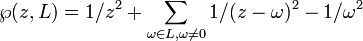
Lorsque le nombre complexe z parcourt
Les coefficients de la courbe g2 et g3 sont donnés par les valeurs de deux séries convergentes associées traditionnellement à un réseau L, les séries d'Eisenstein de poids 2 et 3:
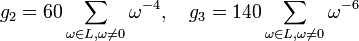
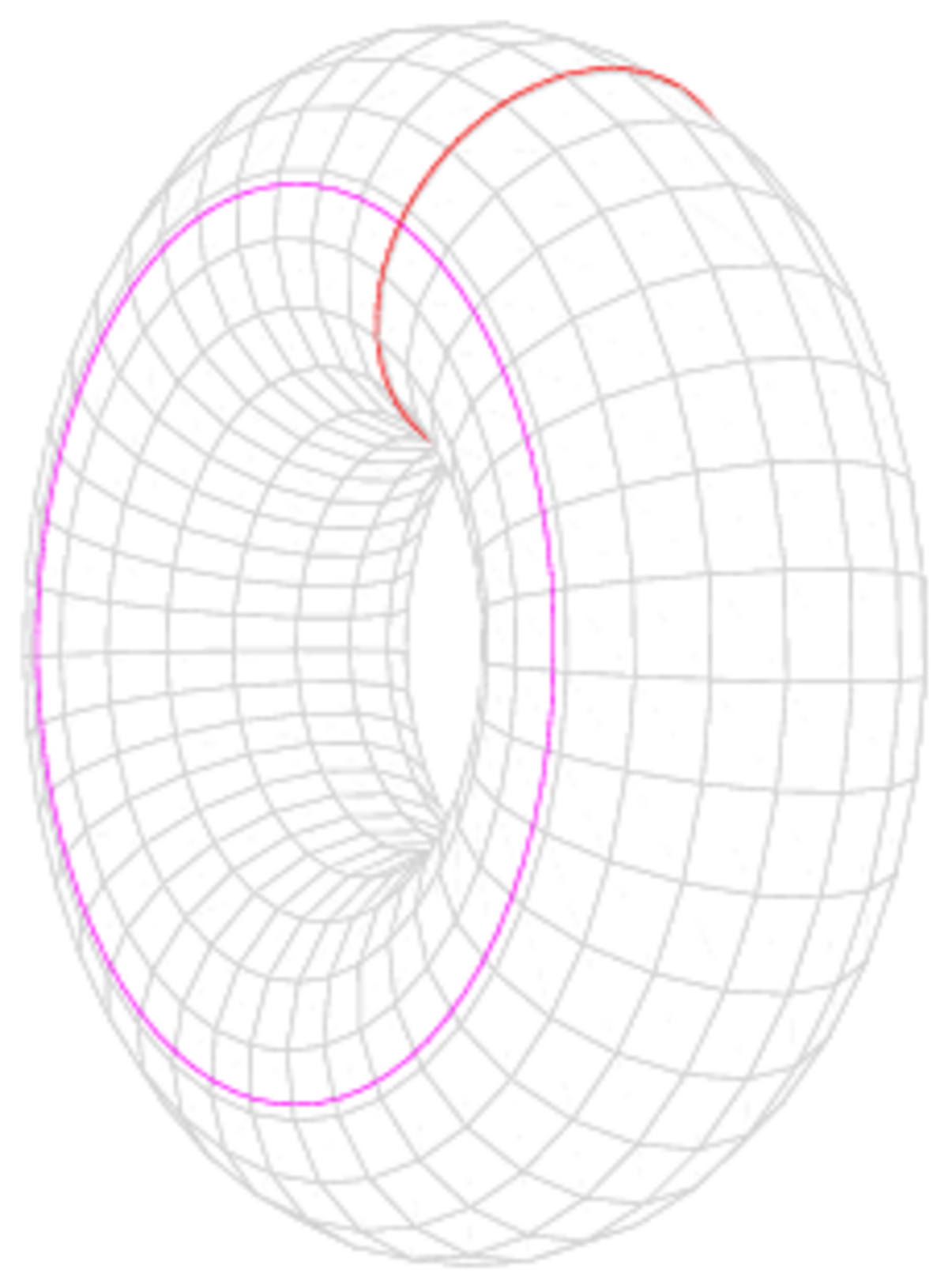
La situation est donc analogue à celle du paramétrage des points d'un cercle par les fonctions cos et sin. Dans le cas du cercle, d'équation y2 = 1 − x2, les fonctions qui le paramètrent sont périodiques de période 2π. Dans le cas d'une courbe elliptique, les fonctions de Weierstrass ont pour périodes indépendantes les deux nombres générateurs du réseau L.
On a plus précisément :
Théorème — Soit E une courbe elliptique définie sur
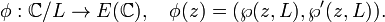
Autrement dit, la courbe elliptique est isomorphe à un tore complexe (on doit se rappeler que la 'droite' complexe, de dimension 1 comme courbe définie sur
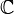
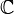
La forme différentielle dx / y est holomorphe et non nulle en tout point de la courbe ; elle correspond à la forme
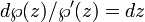
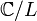
| ω1 = | ∫ | dx / y |
| α |
et
| ω2 = | ∫ | dx / y |
| β |
sont deux périodes indépendantes, qui engendrent le réseau L.
La loi de groupe est directement visible sur le tore
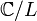
Une application géométrique : le théorème de clôture de Poncelet
Parmi les nombreuses applications des courbes elliptiques, on peut mentionner le théorème de clôture de Poncelet par rapport à deux coniques. Soient deux coniques du plan complexe projectif non dégénérées et sans point d'intersection double, qu'on peut représenter par les deux matrices M et N des formes quadratiques associées. Si en partant d'un point A sur l'une d'elles, on trace la tangente AA' à l'autre conique, menée de ce point, elle recoupe la première conique en un autre point B et on peut réitérer en construisant l'autre tangente BB' menée par B à la deuxième conique, etc.
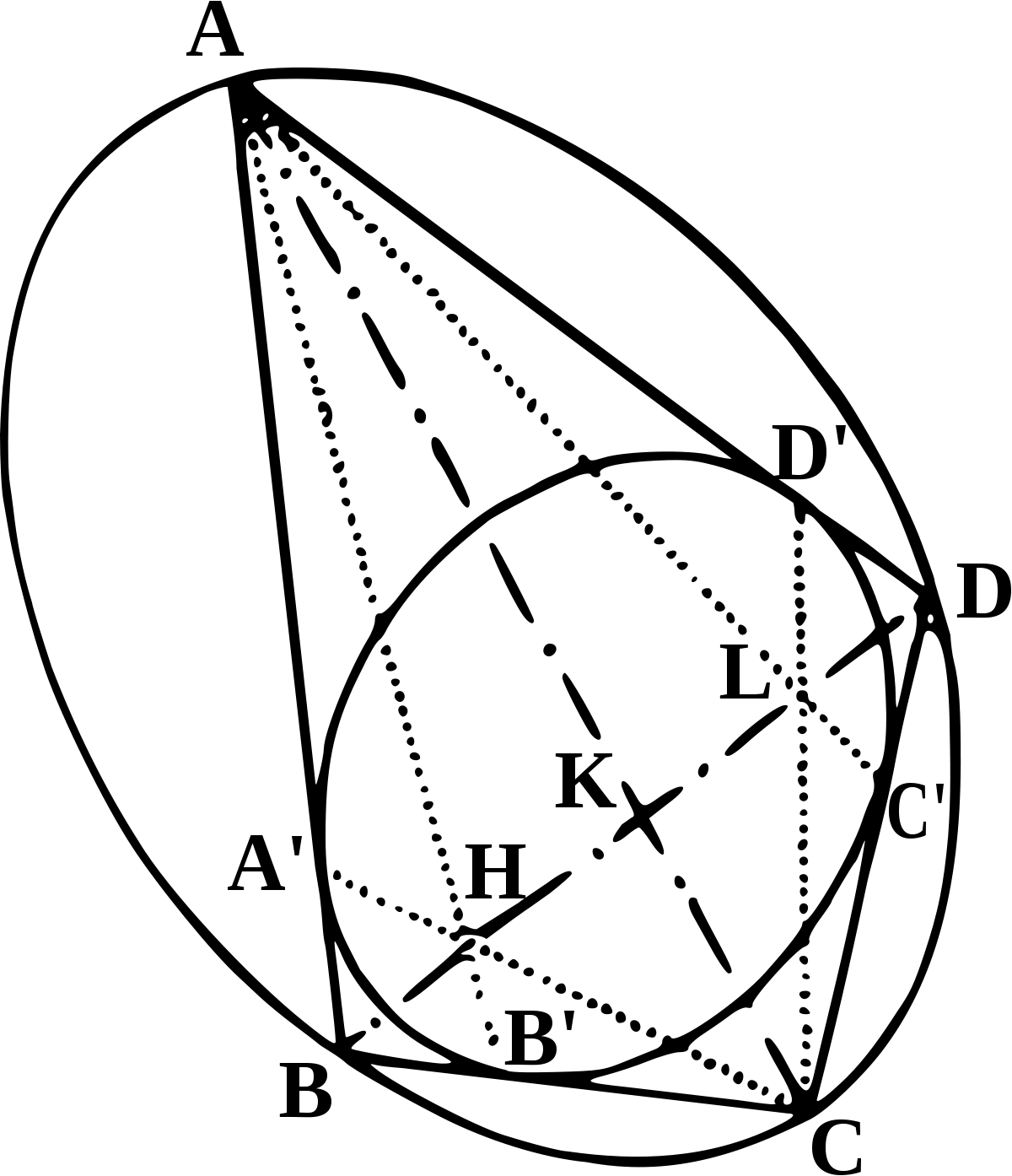
Le théorème de clôture de Poncelet dit que si cette construction boucle, pour un point de départ A donné, après un nombre fini d'étapes (autrement dit si la construction ramène au point de départ, formant un polygone à un nombre déterminé de côtés), elle boucle, avec le même nombre de côtés, pour n'importe quel point de départ. Cette propriété de clôture de la construction ne dépend donc pas du point de départ, mais seulement de la disposition des deux coniques.
On peut utiliser les courbes elliptiques pour donner une preuve directe de ce résultat : les points d'une conique sont paramétrables par un nombre x, la tangente est un élément de la conique duale représentable par un nombre y ; en choisissant bien le système de coordonnées, on montre que la relation entre x et y est y2 = det(Mx + N), ce qui, en développant le déterminant, est l'équation d'une courbe elliptique. On montre de plus qu'on passe de (A,AA') à (B,BB') par l'addition (au sens de l'addition sur la courbe elliptique) d'un point P0 qui ne dépend pas de A, mais seulement de l'équation de la courbe elliptique, c'est-à-dire des coniques elles-mêmes. La construction boucle si et seulement si ce point P0 est un point de torsion sur la courbe elliptique. Cette interprétation permet d'ailleurs de déterminer des paires de coniques supportant des polygones de Poncelet à un nombre voulu de côtés.