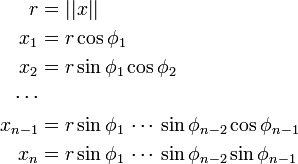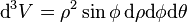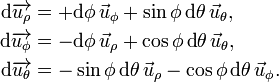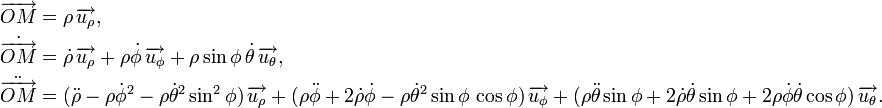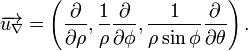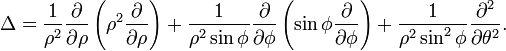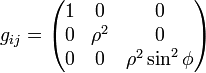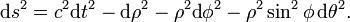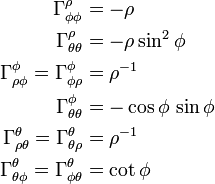Coordonnées sphériques - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Utilisation - Définition et propriétés élémentaires - Généralisation - Propriétés

Généralisation

Soit un espace vectoriel normé de dimension n finie. Pour un point x de cet espace, de coordonnées (x, …, x), on définit les coordonnées sphériques (r, ϕ, …, ϕ) par

\begin{align} r &= ||x||\\ x_1 &= r\cos\phi_1\\ x_2 &= r\sin\phi_1 \cos \phi_2\\ \cdots\\ x_{n-1} &= r\sin\phi_1\,\cdots\,\sin\phi_{n-2}\cos\phi_{n-1}\\ x_n &= r\sin\phi_1\,\cdots\,\sin\phi_{n-2}\sin\phi_{n-1} \end{align}

Les coordonnées sphériques constituent le cas particulier n = 3 et les polaires n = 2 ; on pourra consulter la section correspondante de l'article 3-sphère pour le cas n=4.

Propriétés

Propriétés différentielles

Différentielles

Le volume infinitésimal s'écrit

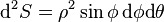
et la surface à ρ constant est $\text{d}^2 S = \rho^2\sin\phi\,\text{d}\phi\text{d}\theta$ .

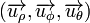
Les vecteurs de la base comobile $(\overrightarrow{u_\rho}, \overrightarrow{u_\phi}, \overrightarrow{u_\theta})$ ont pour différentielles :

\begin{align} \text{d}\overrightarrow{u_\rho} &= + \text{d}\phi\,\vec{u}_\phi + \sin\phi\,\text{d}\theta\,\vec{u}_\theta,\\ \text{d}\overrightarrow{u_\phi} &= -\text{d}\phi\,\vec{u}_\rho + \cos\phi\,\text{d}\theta\,\vec{u}_\theta,\\ \text{d}\overrightarrow{u_\theta} &= -\sin\phi\,\text{d}\theta\,\vec{u}_\rho - \cos\phi\,\text{d}\theta\,\vec{u}_\phi. \end{align}

Cinématique

Les quantités cinématiques, position, vitesse et accélération s'en déduisent :

\begin{align} \overrightarrow{OM} &= \rho\,\overrightarrow{u_\rho},\\ \dot{\overrightarrow{OM}} &= \dot\rho\,\overrightarrow{u_\rho} + \rho\dot\phi\,\overrightarrow{u_\phi} + \rho\sin\phi\,\dot\theta\,\overrightarrow{u_\theta},\\ \ddot{\overrightarrow{OM}} &= (\ddot\rho-\rho\dot\phi^2-\rho\dot\theta^2\sin^2\phi)\,\overrightarrow{u_\rho} + (\rho\ddot\phi + 2\dot\rho\dot\phi - \rho\dot\theta^2\sin \phi\,\cos\phi) \,\overrightarrow{u_\phi} + (\rho\ddot\theta\sin\phi + 2\dot\rho\dot\theta\sin\phi + 2\rho\dot\phi\dot\theta\cos \phi) \,\overrightarrow{u_\theta}. \end{align}

Opérateurs différentiels

L'opérateur nabla, servant au calcul du gradient, de la divergence et du rotationnel s'écrit

Le laplacien s'en déduit :

Tenseurs usuels

Le tenseur métrique s'écrit

g_{ij} = \left(\begin{matrix} 1 & 0 & 0\\ 0 & \rho^2 & 0\\ 0 & 0 & \rho^2 \sin^2\phi \end{matrix}\right)

et l'intervalle

Les éléments non nuls du symbole de Christoffel sont

\begin{align} \Gamma^{\rho}_{\phi\phi} &= -\rho\\ \Gamma^{\rho}_{\theta\theta} &= -\rho \sin^2\phi\\ \Gamma^{\phi}_{\rho\phi} = \Gamma^{\phi}_{\phi\rho} &= \rho^{-1}\\ \Gamma^{\phi}_{\theta\theta} &= -\cos\phi\,\sin\phi\\ \Gamma^{\theta}_{\rho\theta} = \Gamma^{\theta}_{\theta\rho} &= \rho^{-1}\\ \Gamma^{\theta}_{\theta\phi} = \Gamma^{\theta}_{\phi\theta} &= \cot\phi \end{align}

Relation avec les autres systèmes de coordonnées usuels

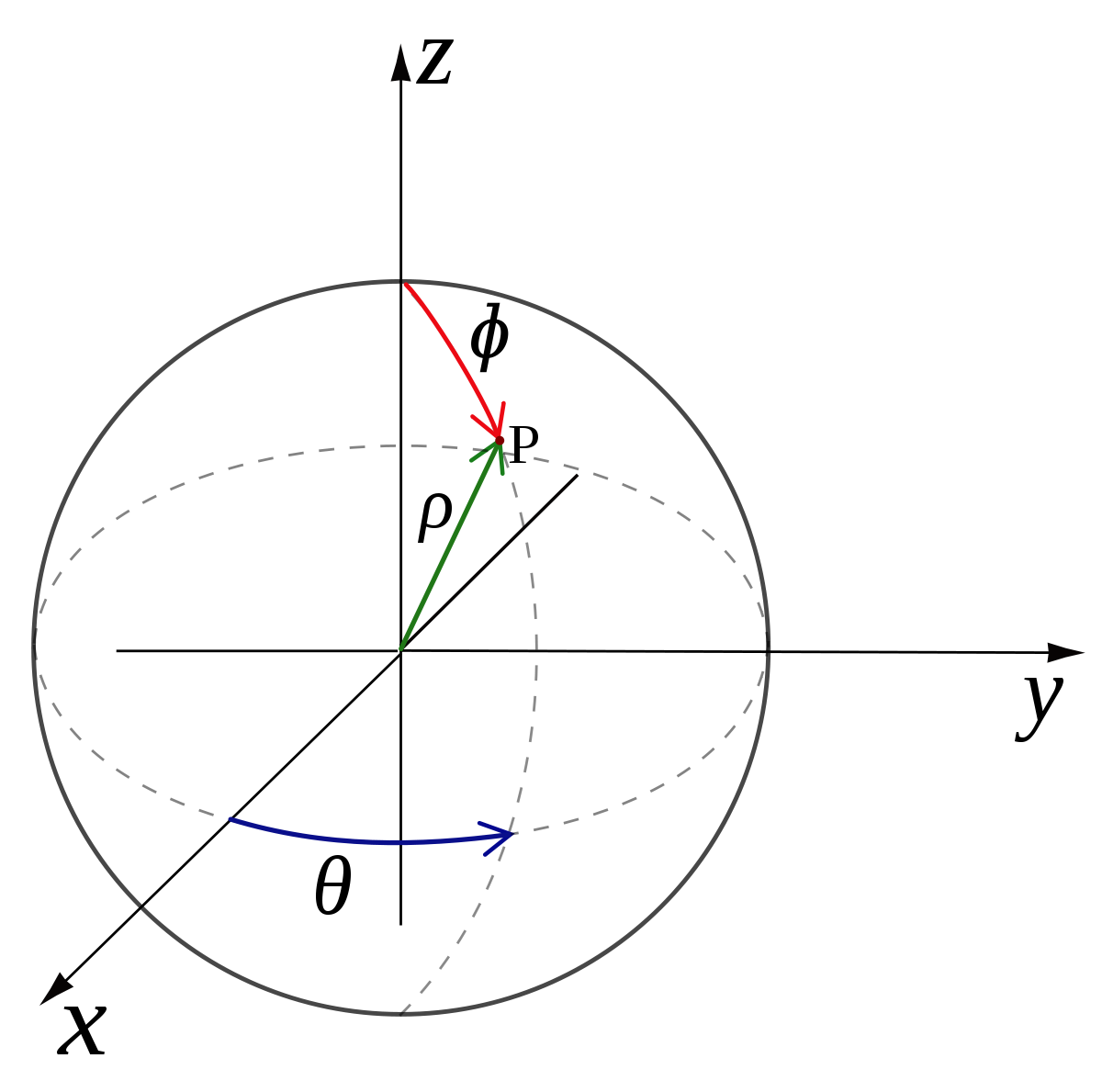
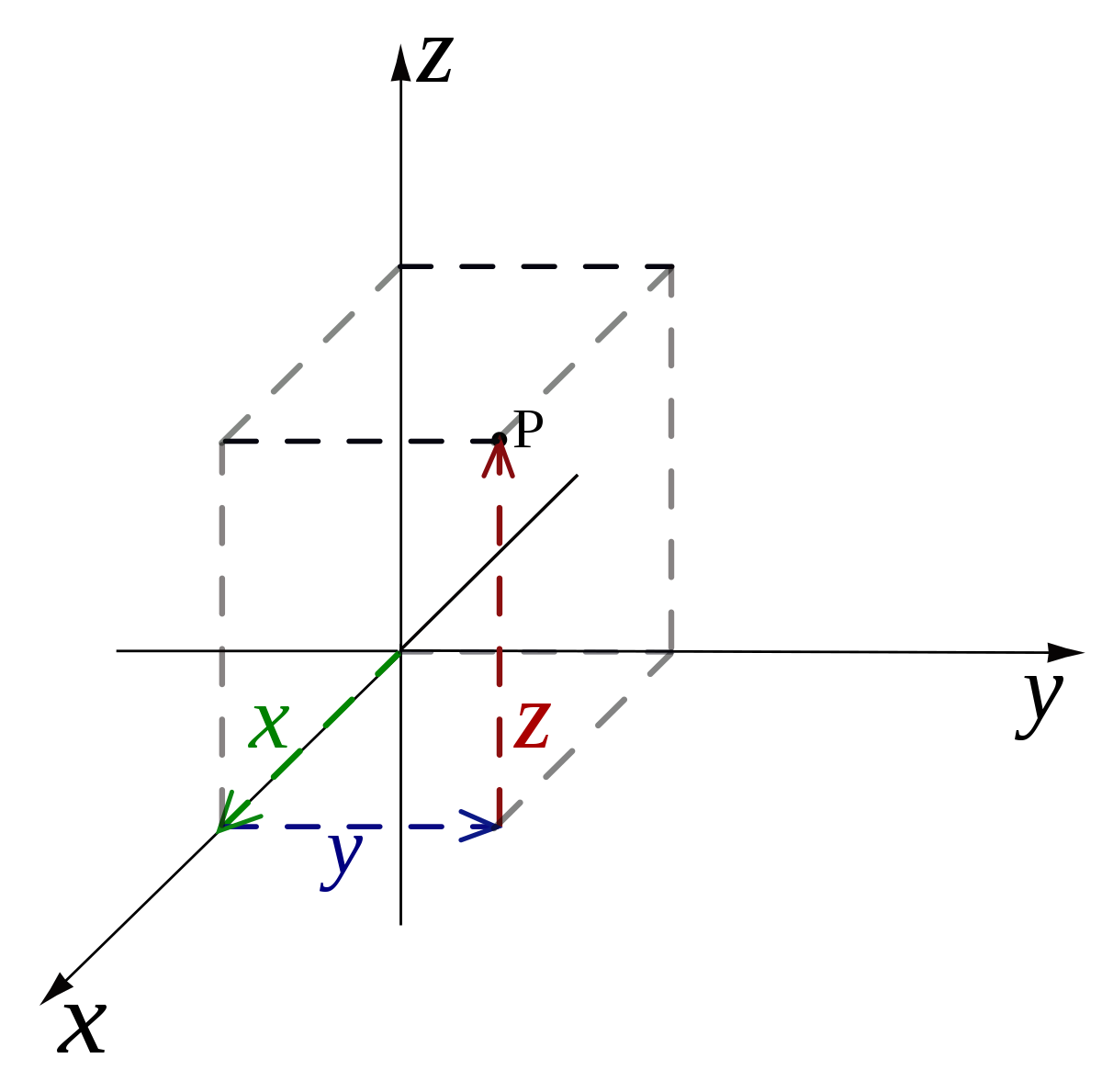
Les coordonnées cartésiennes (x, y, z), cylindriques (r, θ′, z) et sphériques, lorsqu'elles sont définies par rapport au même repère cartésien (O, x, y, z) suivent les lois de transformations données ci-dessous.

Système de coordonnées	Depuis les coordonnées sphériques	Vers les coordonnées sphériques
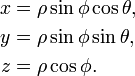
Coordonnées cartésiennes	$\begin{align} x &= \rho \sin\phi \cos\theta,\\ y &= \rho \sin\phi \sin\theta,\\ z &= \rho \cos\phi. \end{align}$	$\begin{align} \rho &= \sqrt{x^2+y^2+z^2},\\ \phi &= \arccos(z/\rho)\\ \theta &= \begin{cases}\arccos\frac{x}{\sqrt{x^2+y^2}} & \mathrm{si}\ y\geq0, \\[,5em] 2\pi-\arccos\frac x{\sqrt{x^2+y^2}} & \mathrm{si}\ y < 0;\end{cases} \end{align}$
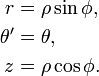
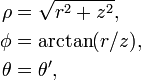
Coordonnées cylindriques	$\begin{align} r &= \rho \sin\phi,\\ \theta^\prime &= \theta,\\ z &= \rho \cos\phi. \end{align}$	$\begin{align} \rho &= \sqrt{r^2+z^2},\\ \phi &= \arctan(r/z),\\ \theta &= \theta^\prime, \end{align}$

Dans le tableau ci-dessus arctan(y, x) est le prolongement classique sur les différents quadrants de arctan(y/x) pour x et y positifs.

Coordonnées sphériques

Coordonnées cartésiennes

Coordonnées cylindriques

Définition et propriétés élémentaires

- Introduction - Utilisation - Définition et propriétés élémentaires - Généralisation - Propriétés

Comment des impacts géants vaporisent les corps planétaires ☄️

Les Américains riches vivent moins longtemps que les Européens pauvres 💰

Attention à ce riz naturellement riche en arsenic 🍚

L'intelligence artificielle contre la mort subite 💀

L'inévitable formation d'un océan de magma basal sur Terre 🔥

Découverte d'une plante étrange sans chlorophylle 🌱

Existe-t-il des mélodies naturelles ? 🎶

Cette exoplanète présente une signature de vie bien plus forte que celle de la Terre 👽

L'origine énigmatique des rayons cosmiques les plus énergétiques ⚡

Le diagnostic de l'autisme remis en cause par l'intelligence artificielle 🩺

Imprimer en 3D avec la lumière du soleil ☀️

La pollution atmosphérique nuit gravement au cerveau 🧠

Le trou noir supermassif Ansky vient de se réveiller ⚫

Voici ce qui rend notre cerveau vraiment unique 🧠

Asymétrie matière-antimatière: une nouvelle pièce du puzzle dévoilée 🧩

Neige en inuit, goût en japonais... comment les langues décomposent la réalité ? 💬

La physique révèle les secrets d'un strike parfait au bowling 🎳

Le TDAH associé à la démence 🧠

Découverte d'une nouvelle forme d'intrication quantique, une première en 20 ans ⚛️

Le régime cétogène montre des surprises sur le cholestérol 🧐

Un tango observationnel révèle une Super-Terre 🔭

Cette expérience montre que la graisse brune augmente fortement la longévité 🕒

L'Univers comme jamais vu auparavant: les révélations du fond diffus cosmologique 🔭

C'est sérieux: de la bave pourrait révolutionner la conception de bioplastiques 🪱

Découverte: le trou noir central de notre galaxie pourrait anéantir la vie sur Terre 💥

Etude scientifique: ces aliments nous font vieillir 🍽️

Pourquoi notre visage est-il plus petit et délicat que celui des Néandertaliens ? 🤔

A 18 ans, il découvre 1,5 million d'objets célestes inconnus avec son algorithme d'IA 🌟

Que sont ces objets rouges et aplatis, qualifiés d'UFOs par les astronomes ? 🔭

Une méthode simple pour améliorer les performances en mathématiques 🧮

Que sont ces étranges éclairs rouges photographiés au-dessus de l'Himalaya ? ⚡

Nous descendons non pas d'un, mais d'au moins deux groupes anciens 🧬

Un nuage géant de 160 000 soleils découvert dans notre Voie lactée 🔭

Connaissez-vous le rat-kangourou musqué, ce marsupial à la démarche unique ? 🦘

Comment une poignée de traders a fait s'effondrer deux cryptomonnaies 📉

Première cartographie titanesque d'un cerveau, avec 500 millions de connexions neuronales 🧠

Cette double supernovae proche est inexorable, voici la date... qui va vous surprendre 💥

Un océan phosphorescent: comment s'explique ce phénomène rare et féerique ? 🌊

L'ELT pourrait-il découvrir une vie extraterrestre dès 2028 ? 🔭

Cet édulcorant tue les superbactéries résistantes 🍬

Les neutrinos, la clé de la gravité quantique ? 👀

En Italie, les éruptions explosives de ce volcan déjouent les pronostics 🌋

Que sont ces spaghettis au cœur de notre galaxie ? 🔭

Des scientifiques ont créé une "bombe intelligente" contre le cancer 🎯

Les nanoplastiques, l'amiante du 21ème siècle ? 🔬

Compétition cellulaire: des forces sculptent nos tissus 🛠️

Le climat en Europe et au États-Unis pourrait changer bien plus radicalement que supposé 🌍

Découverte: ce dinosaure avait des poches d'air dans les os 🦴

La vie sur Titan, si elle existe, ressemblerait à quoi ? 🪐

Magnétisme et biologie s'allient contre le cancer 🧲

Page générée en 0.099 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise