Coordonnées polaires - Définition
La liste des auteurs de cet article est disponible ici.
Introduction

Les coordonnées polaires sont, en mathématiques, un système de coordonnées à deux dimensions, dans lequel chaque point du plan est entièrement déterminé par un angle et une distance. Ce système est particulièrement utile dans les situations où la relation entre deux points est plus facile à exprimer en termes d’angle et de distance, voir par exemple le pendule. Dans ce cas, le système des coordonnées cartésiennes, plus familier, impliquerait d’utiliser des formules trigonométriques pour exprimer une telle relation.
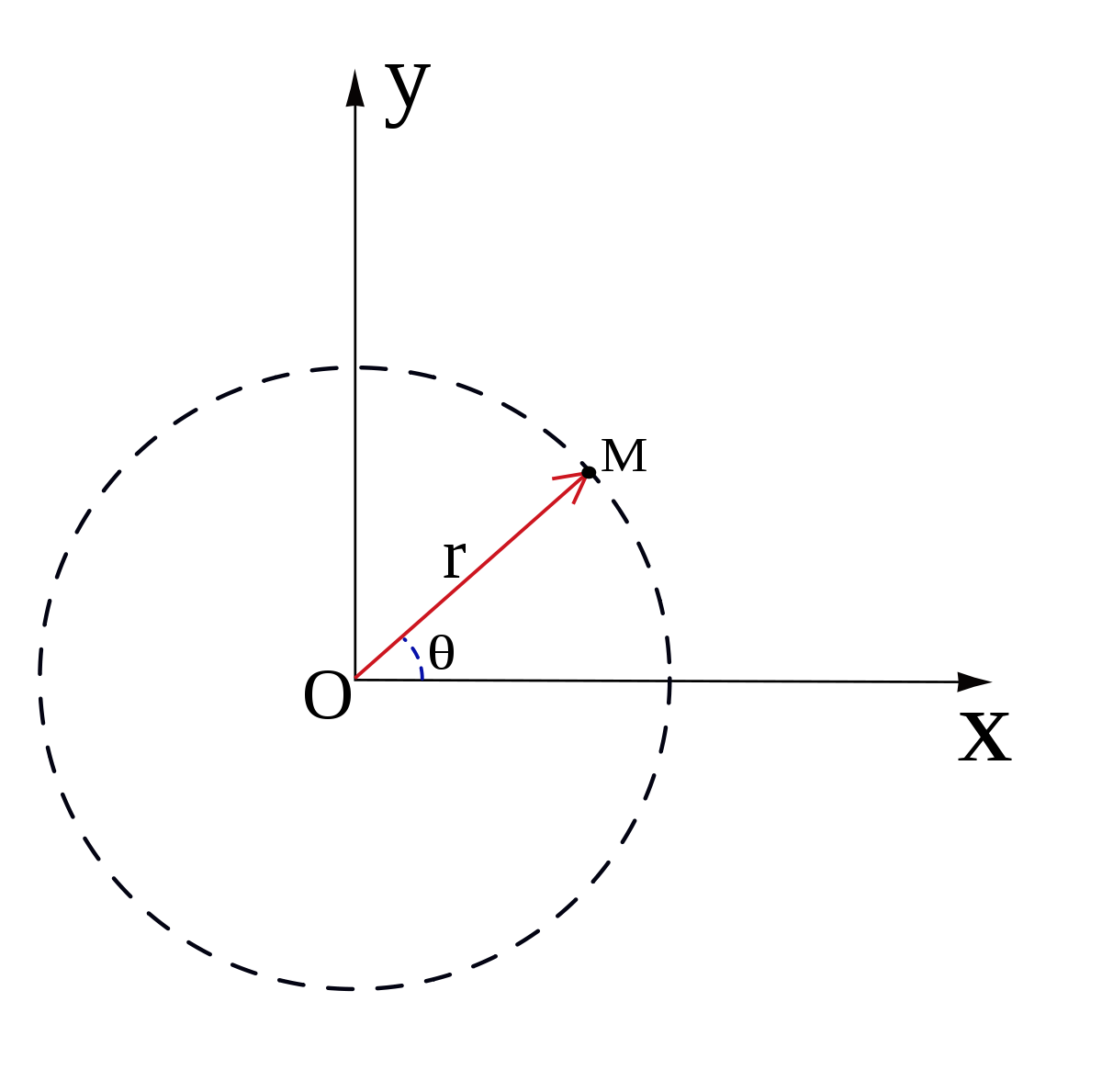
Comme il s’agit d’un système bidimensionnel, chaque point est déterminé par les coordonnées polaires, qui sont la coordonnée radiale et la coordonnée angulaire. La coordonnée radiale (souvent notée r ou ρ, et appelée rayon) exprime la distance du point à un point central appelé pôle (équivalent à l’origine des coordonnées cartésiennes). La coordonnée angulaire (également appelée angle polaire ou azimut, et souvent notée t ou θ) exprime la mesure, dans le sens trigonométrique, de l’angle entre le point et la demi-droite d’angle 0°, appelé axe polaire (équivalent à l’axe des abscisses en coordonnées cartésiennes).
Histoire
Le concept d’angle et de rayon était déjà utilisé lors du premier millénaire avant J.C. L’astronome Hipparque créa une table trigonométrique qui donnait la longueur de la corde pour chaque angle, et il utilisait les coordonnées polaires pour établir les positions des étoiles. Dans Des spirales, Archimède étudia la spirale d'Archimède, une fonction mathématique dont le rayon dépend de l’angle. Cependant les grecs ne l’étendront pas à un système de coordonnées complet.
Il existe plusieurs versions de l’introduction des coordonnées polaires comme système de coordonnées formel. Grégoire de Saint-Vincent et Bonaventura Cavalieri ont indépendamment introduit ce concept dans le milieu du dix-septième siècle. Saint-Vincent a écrit sur ce thème en 1625 et a publié son travail en 1647, pendant que Cavalieri publia ses écrits en 1635, une version corrigée vit le jour en 1653. Cavalieri a d’abord utilisé les coordonnées polaires pour résoudre un problème relatif à l’aire sous une spirale d'Archimède. Blaise Pascal usait largement des coordonnées polaires pour calculer la longueur de paraboles.
Dans Méthode des Fluxions (écrit en 1671, publié en 1736) Sir Isaac Newton étudia les transformations entre les coordonnées polaires, qu'il appelait "Seventh Manner; For Spirals", et neuf autres systèmes de coordonnées. Dans le journal Acta Eruditorum (1691), Jacob Bernoulli utilisa un système avec un point et une droite, appelés respectivement le pôle et l'axe polaire. Les coordonnées étaient déterminées par leur distance au pôle et leur angle par rapport à l'axe polaire. Le travail de Bernouilli utilisa même ce système pour déterminer le rayon de courbure de courbes exprimées dans ce système.
Le terme actuel de coordonnées polaires a été attribué à Gregorio Fontana et a été utilisé par les écrivains italiens du XIIIe siècle. Le terme apparait en anglais pour la première fois dans la traduction de 1816 effectuée par George Peacock du Traité du calcul différentiel et du calcul intégral de Sylvestre-François Lacroix. Alexis Clairaut fut le premier à penser à étendre les coordonnées polaires en trois dimensions, et Leonhard Euler a été le premier à vraiment les développer.