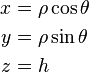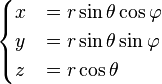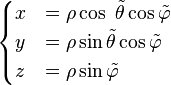Coordonnées polaires - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Histoire - Équation polaire - Placer des points en coordonnées polaires - Calcul infinitésimal - Nombre complexe - Applications - Trois dimensions - Bibliographie

Trois dimensions

Le système de coordonnées polaires peut être étendu à l'espace usuel à trois dimensions de deux manières, ce qui donne le système de coordonnées cylindriques et le système de coordonnées sphériques. Le concept des coordonnées cylindriques est de rajouter une coordonnée de distance, alors que le système sphérique rajoute une coordonnée angulaire.

Coordonnées cylindriques

Un point repéré en coordonnées cylindriques

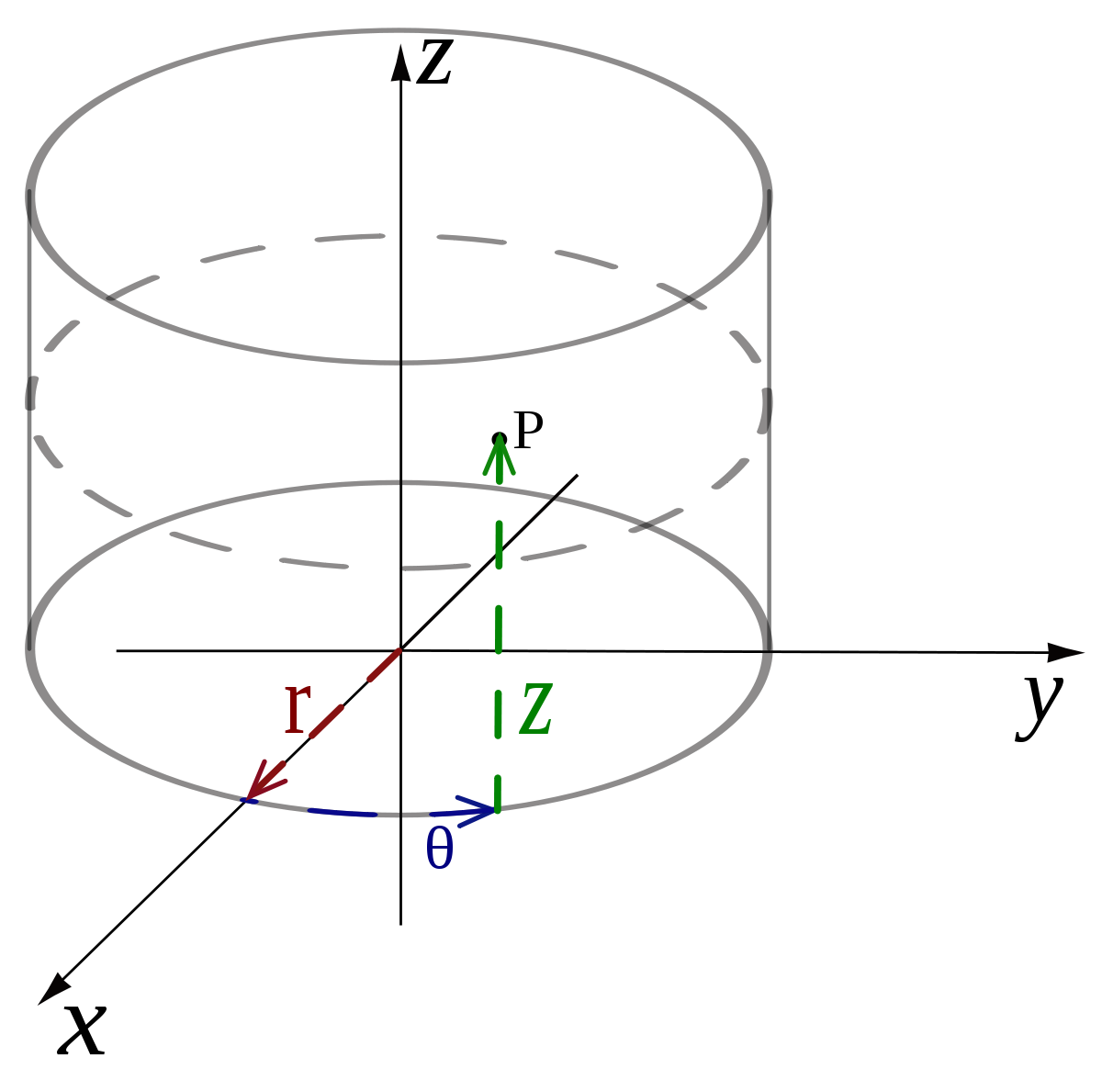
Le système de coordonnées cylindriques est un système de coordonnées qui étend le système de coordonnées polaires à deux dimensions en y ajoutant une troisième dimension qui mesure la hauteur d'un point par rapport au plan repéré par les coordonnées polaires ; de la même manière que l'on étend le système de coordonnées cartésiennes de deux à trois dimensions. La troisième coordonnée est souvent notée h ou z. La notation r étant systématiquement utilisée en coordonnées sphériques (voir ci-dessous), on lui préfère ici la lettre grecque ρ.

Les trois coordonnées cylindriques peuvent être converties en coordonnées cartésiennes par:

\begin{align} x &= \rho \cos\theta \\ y &= \rho \sin\theta \\ z &= h \end{align}

Coordonnées sphériques

Un point repéré en coordonnées sphériques (mathématiques) ; ici la latitude est noté d'un

δ

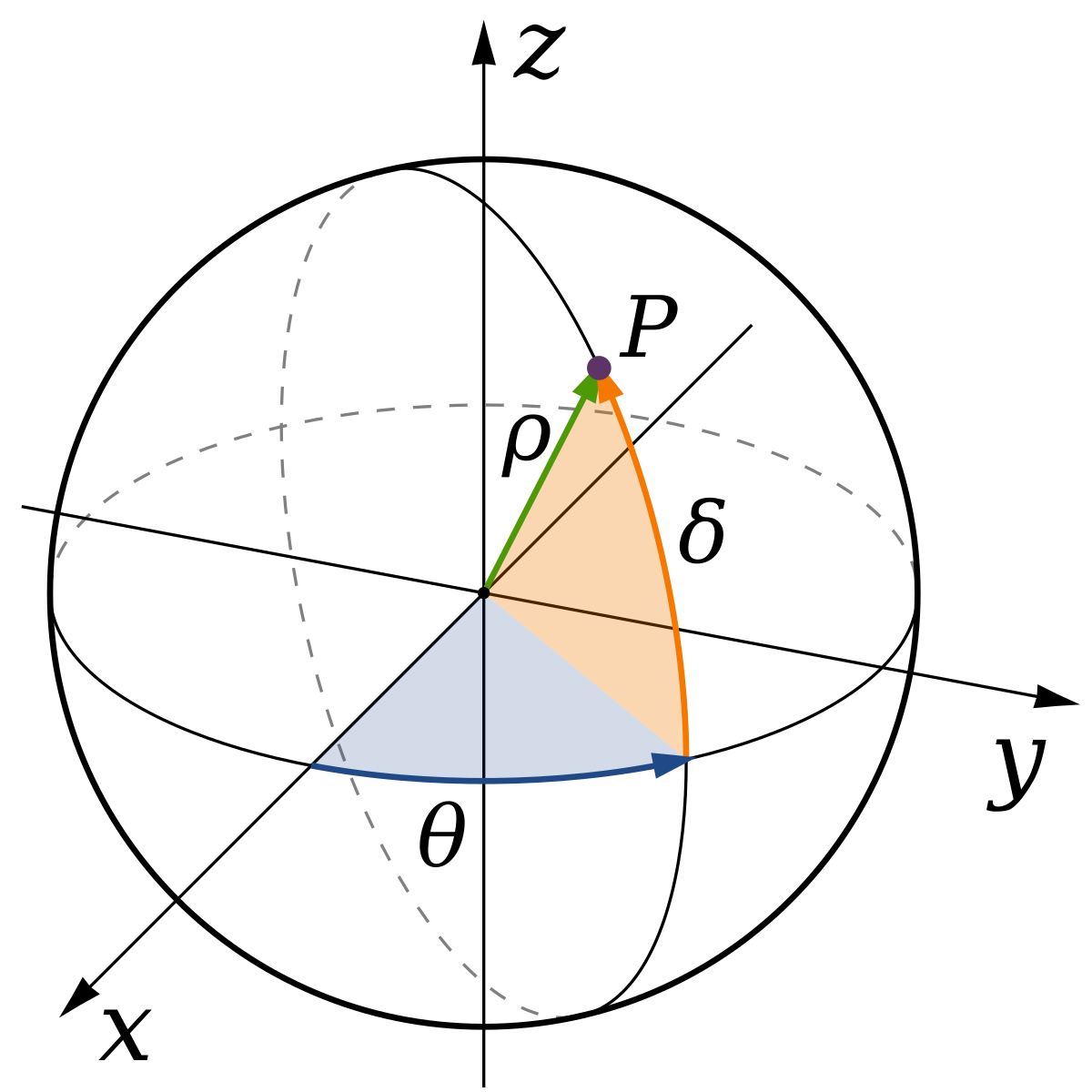
Les coordonnées polaires peuvent aussi être étendues à l'espace tridimensionnel euclidien, suivant diverses conventions de notation.

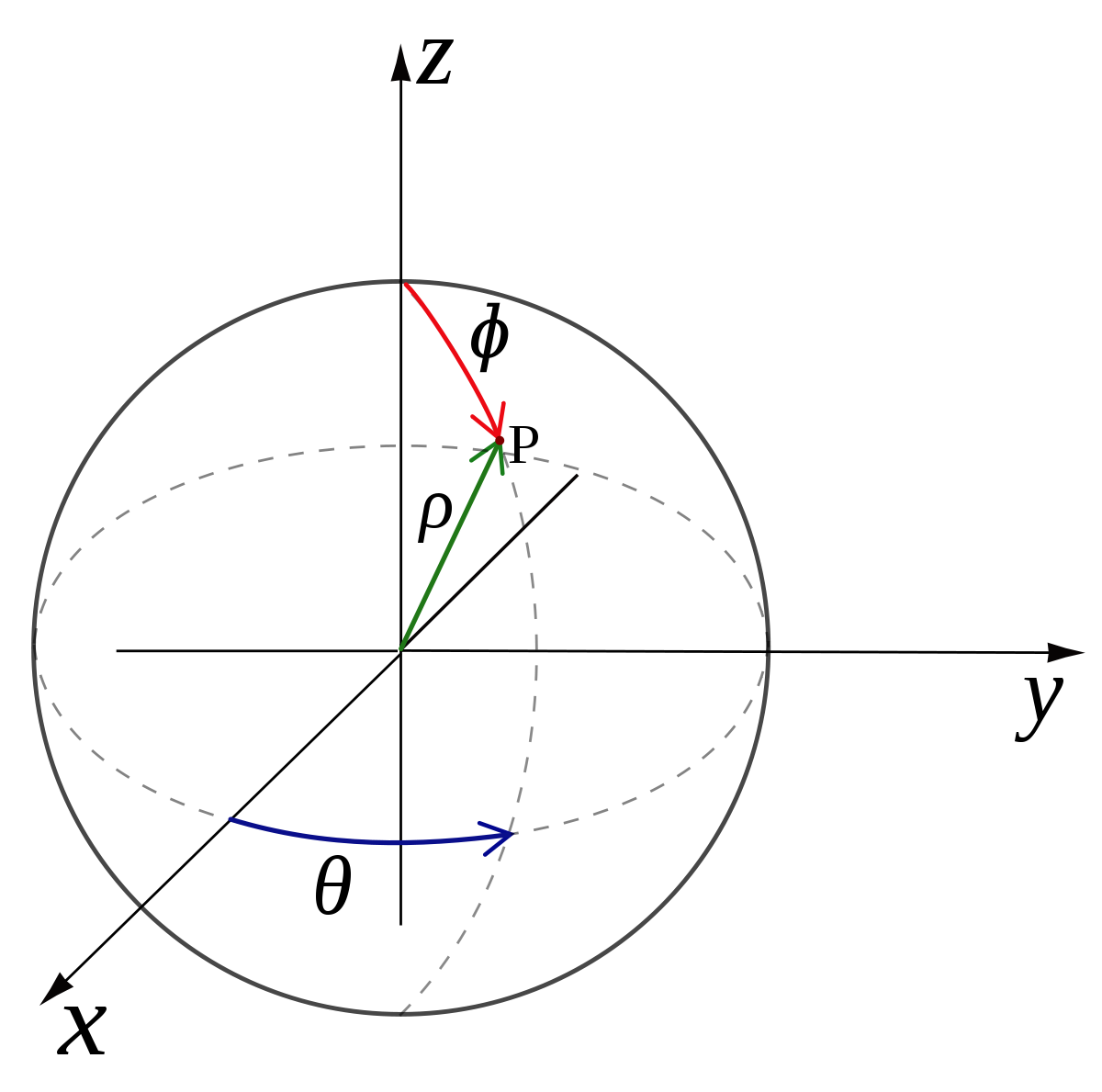
En physique, on utilise le plus souvent les coordonnées (r, θ, φ), où r désigne la distance du point au pôle, θ est l'angle depuis l'axe des z (appelé colatitude ou zénith, compris entre 0° et 180°) et φ est l'angle depuis l'axe des x (comme dans les coordonnées polaires, entre 0° et 360°).

En mathématiques, en nommant les coordonnées ( $ρ$ , $θ$ , $^{ \varphi}$ ), où $ρ$ désigne toujours la distance du point au pôle, alors que $θ$ désigne cette fois la longitude (angle mesuré depuis l'axe des x et compris entre -180° et 180°) et $^{ \varphi}$ la latitude, l'angle depuis le plan équatorial (entre -90° et 90°).

Un système mixte consiste à utiliser dans l'ordre, le rayon, la longitude et ensuite la colatitude, notés toujours ( $ρ$ , $θ$ , φ).

Ces trois systèmes de coordonnées sont des exemples de coordonnées sphériques et ils sont similaires au système utilisé pour se repérer sur la surface de la Terre. Ils ont chacun leur utilité propre mais il faut prendre garde qu'en physique, on nomme $θ$ la colatitude alors qu'en mathématiques, on nomme généralement $θ$ la longitude. La latitude ( $\varphi$ en mathématiques) et la colatitude ( $θ$ en physique) étant complémentaires l'une de l'autre, il est aisé de passer d'un système à un autre.