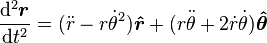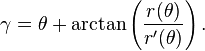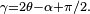Coordonnées polaires - Définition
La liste des auteurs de cet article est disponible ici.
Calcul infinitésimal
Le Calcul infinitésimal peut être appliqué aux équations exprimées en coordonnées polaires. La coordonnée angulaire θ est exprimée en radian, qui est le choix naturel en analyse.
Calcul différentiel et changement de variables polaire
La matrice Jacobienne du changement de variable polaire
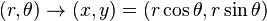
-
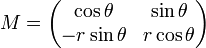
ce qu'on écrit également sous la forme suivante :
-
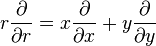
-
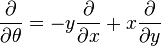
Les dérivées secondes s'expriment également au travers d'une matrice.
Les opérateurs homogènes
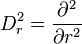
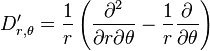
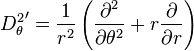
-
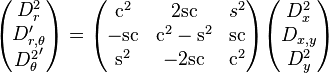
où l'on a noté pour alléger l'expression c en lieu et place de cosθ et s pour sinθ.
On dispose d'ailleurs du même type de changement de dérivées successives au travers de matrices pour tous les ordres de dérivation.
Calcul différentiel et courbe en coordonnées polaire
Pour trouver la pente cartésienne de la tangente à la courbe polaire r(θ) à un point donné, la courbe doit d'abord être exprimée en un système paramétrique :
- x = r(θ)cosθ,
- y = r(θ)sinθ.
Puis nous différentions les deux équations :
-
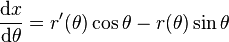
-
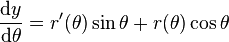
Divisons la deuxième équation par la première et nous obtenons la pente cartésienne de la tangente à la courbe polaire au point (r; r(θ)) :
-
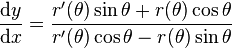
Ainsi l'angle γ, avec l'axe Ox, de la tangente à la courbe polaire au point (r; r(θ)), est donné par la relation :
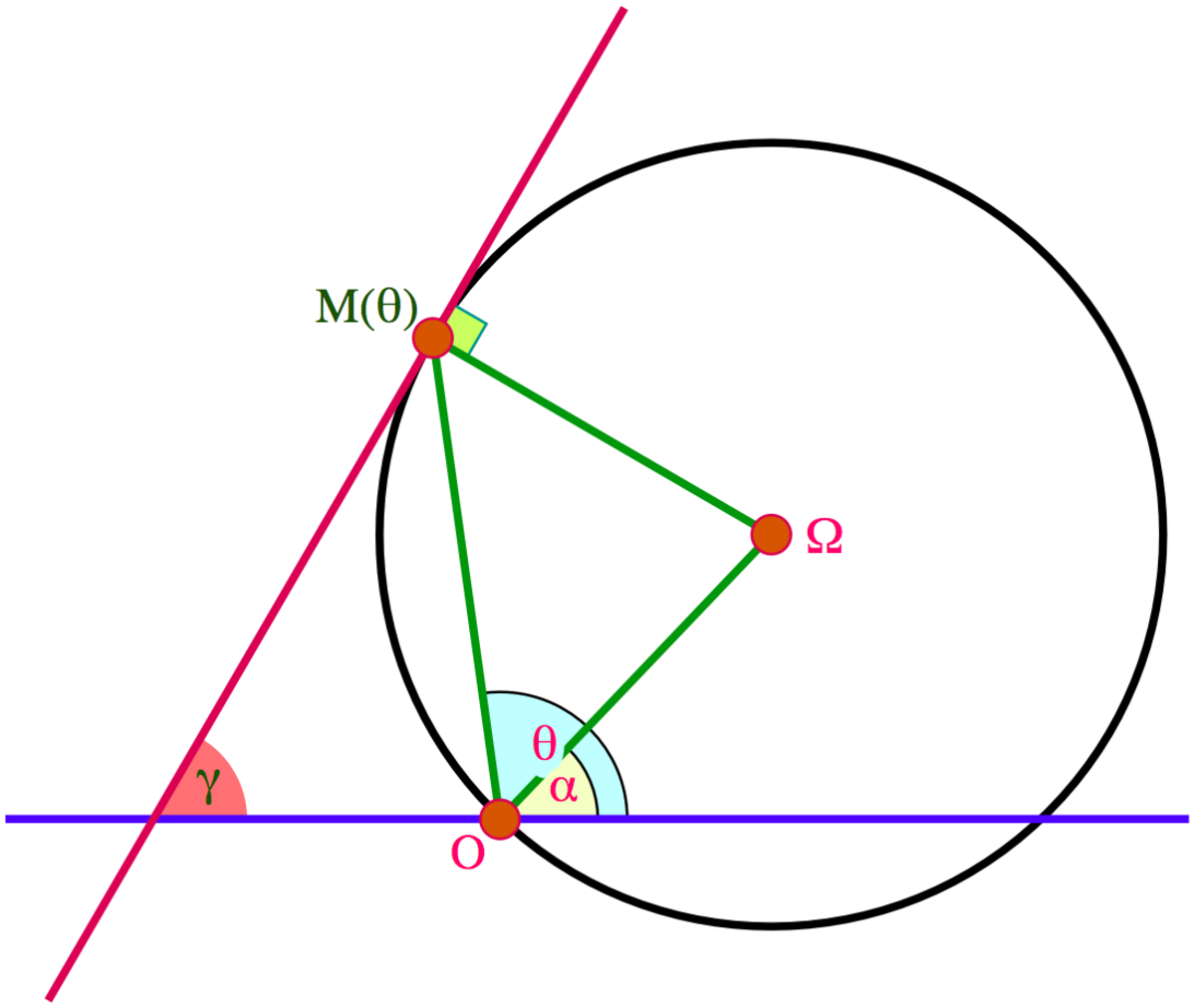
Dans le cas d'un cercle passant par l'origine, de centre Ω = (r; α) et de rayon r, d'équation :
- r(θ) = 2r0cos(θ − α),
la formule donnant γ (voir figure ci-contre) conduit à
- γ = 2θ − α + π / 2,,
ce qui démontre au passage le théorème de l'angle inscrit et de l'angle au centre.
Calcul intégral
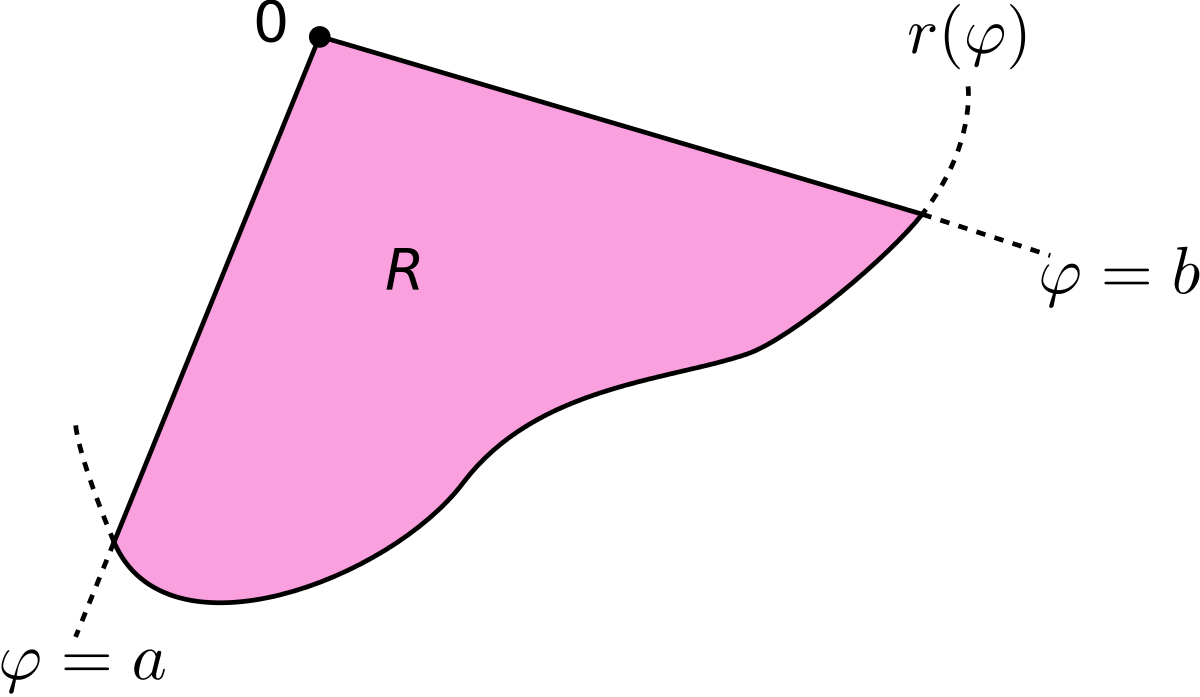
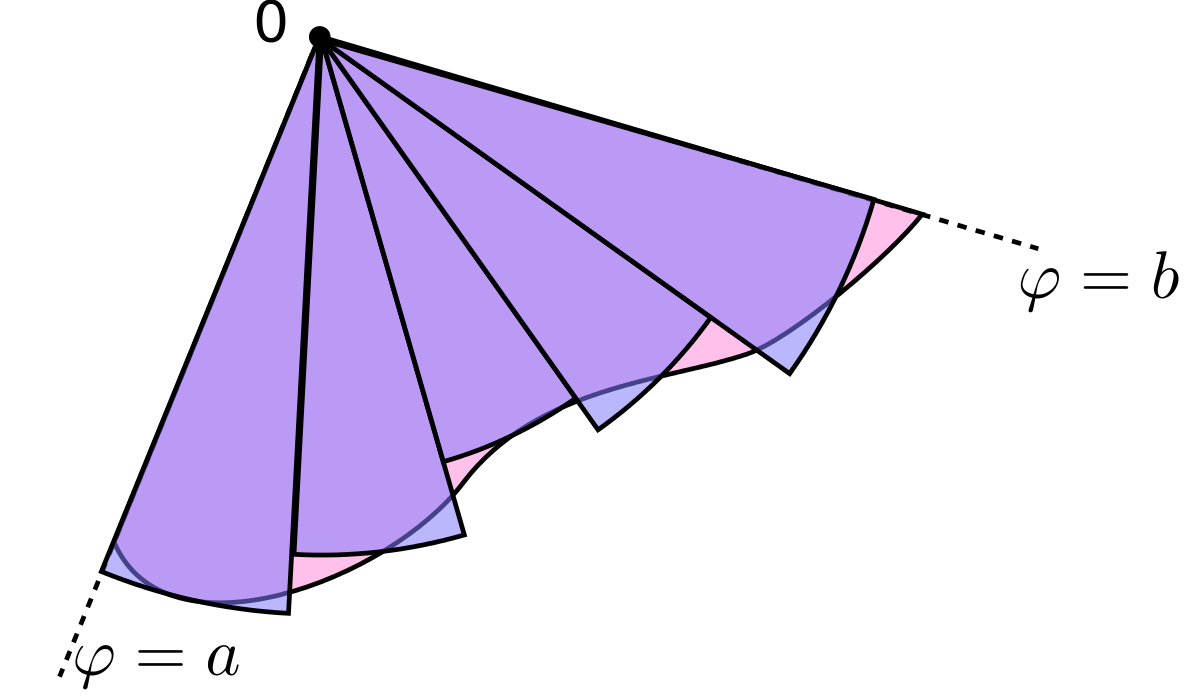
Soit R une surface du plan délimitée par la courbe continue r(θ) et les demi-droites θ = a et θ = b, où 0 < b − a < 2π (a et b étant des réels). Alors la superficie S de cette surface est
-
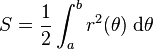
Le résultat peut être retrouvé par le raisonnement suivant. Tout d'abord, l'intervalle [a, b] est subdivisé en n sous-intervalles, où n est un entier positif quelconque. Alors Δθ, la longueur de chaque sous-intervalle, est égal à b - a divisé par n, le nombre de sous-intervalles. Pour chaque sous-intervalle i = 1, 2, ..., n, soit θ le milieu de chaque sous-intervalle i. On peut alors construire un secteur circulaire où le centre est le pôle, de rayon r(θ), d'angle Δθ et de longueur d'arc r(θi) Δθ. La surface S de chaque secteur est donc
-
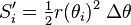
et donc la surface totale de tous les secteurs est:
-
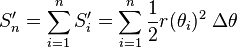
Pour n tendant vers l'infini, l'approximation devient meilleure et cette somme est une somme de Riemann et donc converge vers l'intégrale demandée :
-
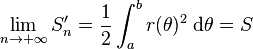
Généralisation
En utilisant les coordonnées cartésiennes, un élément d'aire infinitésimale peut être calculé comme dA = dx dy. La règle du changement de variable pour des intégrales multiples stipule que, lorsque l'on utilise d'autres systèmes de coordonnées, le Jacobien de la matrice de conversion des coordonnées est:
-
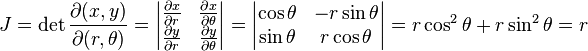
On peut donc voir qu'un élément d'aire infinitésimale peut être vu comme
-
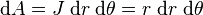
Maintenant une fonction donnée en coordonnées polaires peut être intégrée comme ceci
-
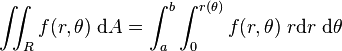
Ici R est la même surface que plus haut, c'est-à-dire la surface comprise entre la courbe r(θ) et les demi-droites θ = a et θ = b.
La formule pour la superficie de R mentionnée plus haut est retrouvé en prenant f la fonction constante égale à 1. L'une des applications étonnantes de ces formules est le calcul de l'intégrale de Gauss
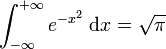
Analyse vectorielle
L'analyse vectorielle peut être également appliquée aux coordonnées polaires. Soit
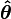
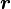
-
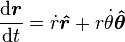
-