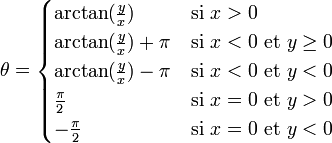Coordonnées polaires - Définition

Placer des points en coordonnées polaires

Les points (3;60°) et (4;210°) en coordonnées polaires

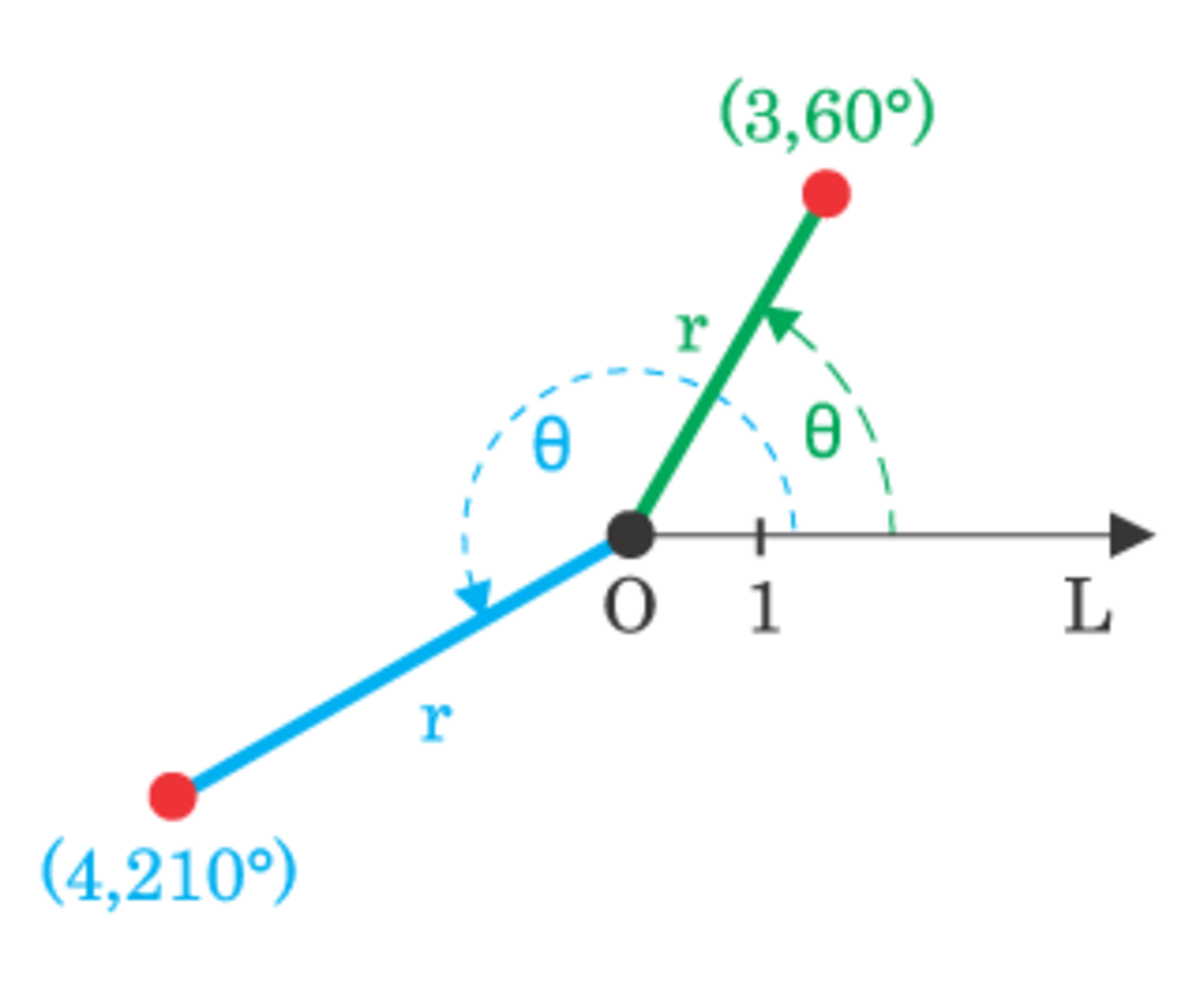
Chaque point du plan est déterminé par les coordonnées polaires, qui sont la coordonnée radiale et la coordonnée angulaire. La coordonnée radiale (souvent notée r ou ρ, et appelé rayon) exprime la distance du point à un point central appelé pôle (équivalent à l’origine des coordonnées cartésiennes). La coordonnée angulaire (également appelée angle polaire ou azimut, et souvent notée t ou θ) exprime la mesure, dans le sens trigonométrique, de l’angle entre le point et la demi-droite d’angle 0°, appelé axe polaire (équivalent à l’axe des abscisses en coordonnées cartésiennes).

Par exemple, le point de coordonnées polaires (3;60 °) sera placé à trois unités de distance du pôle sur la demi-droite d’angle 60 °. Le point (-3 ;-120 °) sera au même endroit car une distance négative sera considérée comme une mesure positive sur la demi-droite opposée par rapport au pôle (tournée de 180 ° par rapport à la demi-droite d’origine).

L’un des aspects importants du système de coordonnées polaires, qui n’est pas présent dans le système cartésien, est qu’il existe une infinité de coordonnées polaires désignant un même et unique point. En effet, on peut rajouter des mesures d’un tour complet sans affecter l’emplacement du point. Par exemple, le point (3;420 °) est confondu avec le point (3;60 °). En général, le point (r; θ) peut être représenté par (r; θ ± n × 360°) ou (−r; θ ± (2 n + 1)180°), où n est un entier quelconque.

Les coordonnées arbitraires (0; θ) sont conventionnellement utilisées pour représenter le pôle, sans se soucier de la valeur attribuée dans ce cas à l’angle θ, un point de rayon r = 0 sera toujours sur le pôle. Pour obtenir un unique représentant du point, on limite le rayon aux réels positifs et l’angle entre -180 ° et 180 ° (ou 0 ° et 360 °), ou si l’on utilise les radians entre –π et π (ou 0 et 2π). On dit que l’angle est donné modulo 360 ° ou 2π.

L’angle en notation polaire est généralement donné en degrés ou radians, en utilisant la convention 2π=360 °. Le choix dépend du contexte. En navigation, les degrés sont de rigueur, alors que certaines applications physiques (comme l’étude des rotations en mécaniques) et la plupart des mathématiques utilisent les radians.

Conversion entre système polaire et cartésien

Un schéma illustrant les formules de conversions

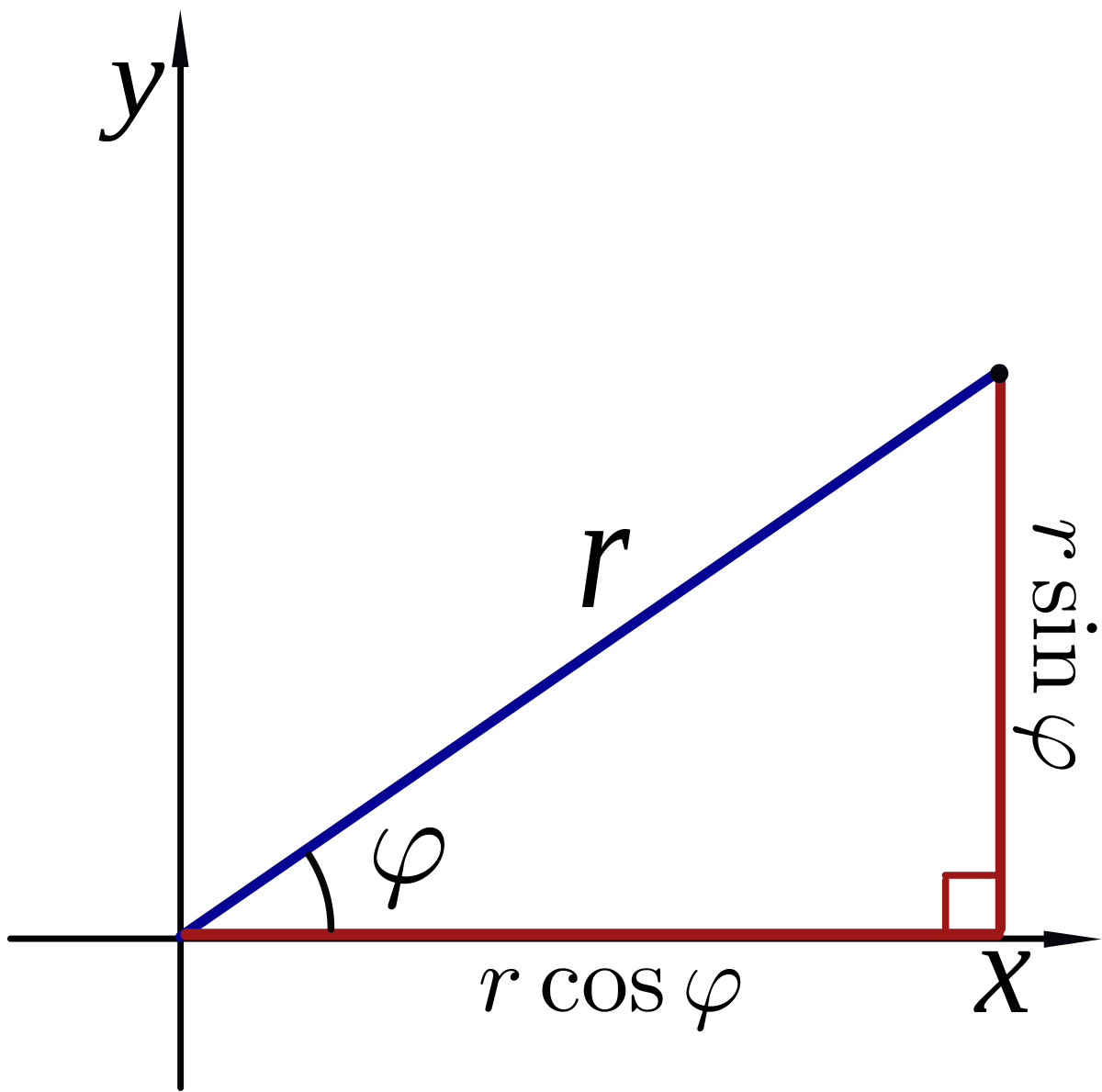
Les deux coordonnées polaires r et θ peuvent être converties en coordonnées cartésiennes x et y en utilisant les fonctions trigonométriques sinus et cosinus :

x = rcosθ

y = rsinθ

Deux coordonnées cartésiennes x et y permettent de calculer la première coordonnée polaire r par :

(par une simple application du théorème de Pythagore).

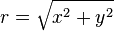
Pour déterminer la seconde (l’angle θ), nous devons distinguer deux cas :

• Pour r = 0, l’angle peut prendre n’importe quelle valeur réelle.
• Pour r ≠ 0, pour obtenir une unique valeur de θ, on se restreint à l’intervalle [0; 2 π[ (ou de manière équivalente ]-π; π]).

Pour obtenir θ dans l’intervalle [0; 2 π[, on utilise les formules suivantes (arctan désigne la réciproque de la fonction tangente) :

Pour l’obtenir dans l’intervalle ]-π; π], on utilise les formules :

Pour obtenir θ dans l’intervalle [ − π;π[, on peut également utiliser la formule suivante, plus concise :

,

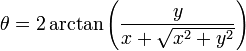
qui est valable pour tout point du plan à l'exception du demi-axe des abscisses (x', O].