Coordonnées polaires - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Histoire - Équation polaire - Placer des points en coordonnées polaires - Calcul infinitésimal - Nombre complexe - Applications - Trois dimensions - Bibliographie

Équation polaire

Une équation qui définit une courbe algébrique exprimée en coordonnées polaires est connue sous le nom d’équation polaire. Dans la plupart des cas, une telle équation peut être spécifiée en définissant r comme une fonction de θ. La courbe résultante est alors formée des points du type (r(θ); θ) et peut être vue comme le graphe de la fonction polaire r.

Différentes formes de symétries peuvent être déduites de l’équation d’une fonction polaire. Si r(-θ)=r(θ) alors la courbe est symétrique par rapport à l’axe horizontal (les demi-droites 0 ° et 180 °). Si r(π - θ)=r(θ), la courbe sera symétrique par rapport à l’axe vertical (90° et 270°).

À cause du caractère circulaire des coordonnées polaires, beaucoup de courbes peuvent être décrites par une équation polaire simple, alors que leur équation cartésienne serait beaucoup plus compliquée. Quelques courbes polaires les plus connues sont : la spirale d'Archimède, le lemniscate de Bernoulli, le limaçon de Pascal ou encore la cardioïde.

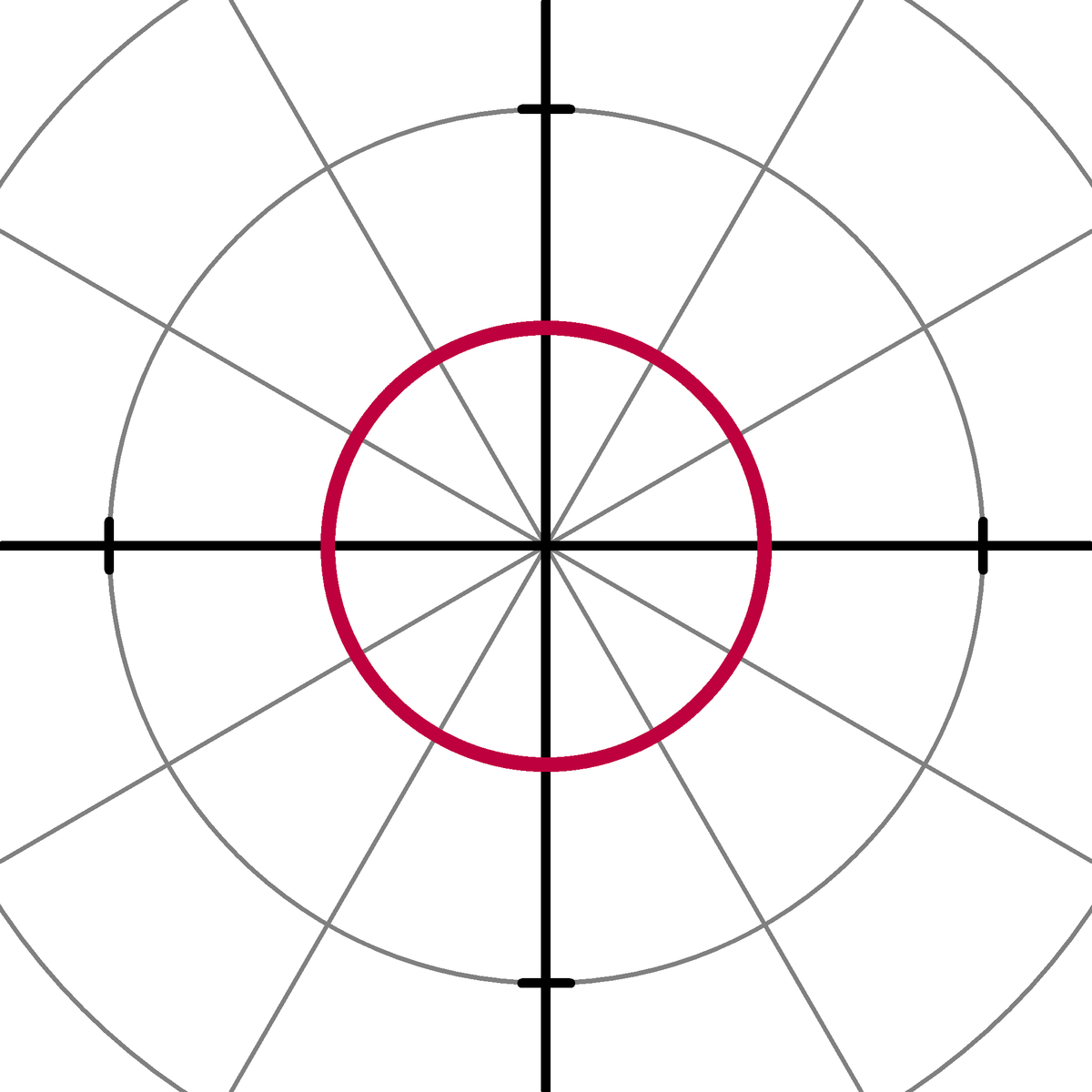
Cercle

Un cercle d'équation r(θ) = 1

L'équation générale d'un cercle de centre (r; φ) et de rayon a est:

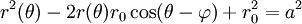$r^2(\theta) - 2 r(\theta) r_0 \cos(\theta - \varphi) + r_0^2 = a^2$ .

Dans de nombreux cas, cette équation est simplifiée. Par exemple,

pour un cercle centré sur le pôle et de rayon a:

r (θ) = a,

pour un cercle passant par l'origine (r = a) :

$r(\theta)=2 r_0 \cos(\theta - \varphi).$

Droite

Une droite radiale (qui passe par le pôle) est représentée par l'équation :

$\theta=\varphi$

où φ est l'angle de la droite. On a φ = arctan m où m est la pente de la droite en coordonnées cartésiennes.

Une droite non radiale qui coupe perpendiculairement au point (r; φ) la droite radiale θ = φ a pour équation:

$r(\theta) = {r_0}\sec(\theta-\varphi)$

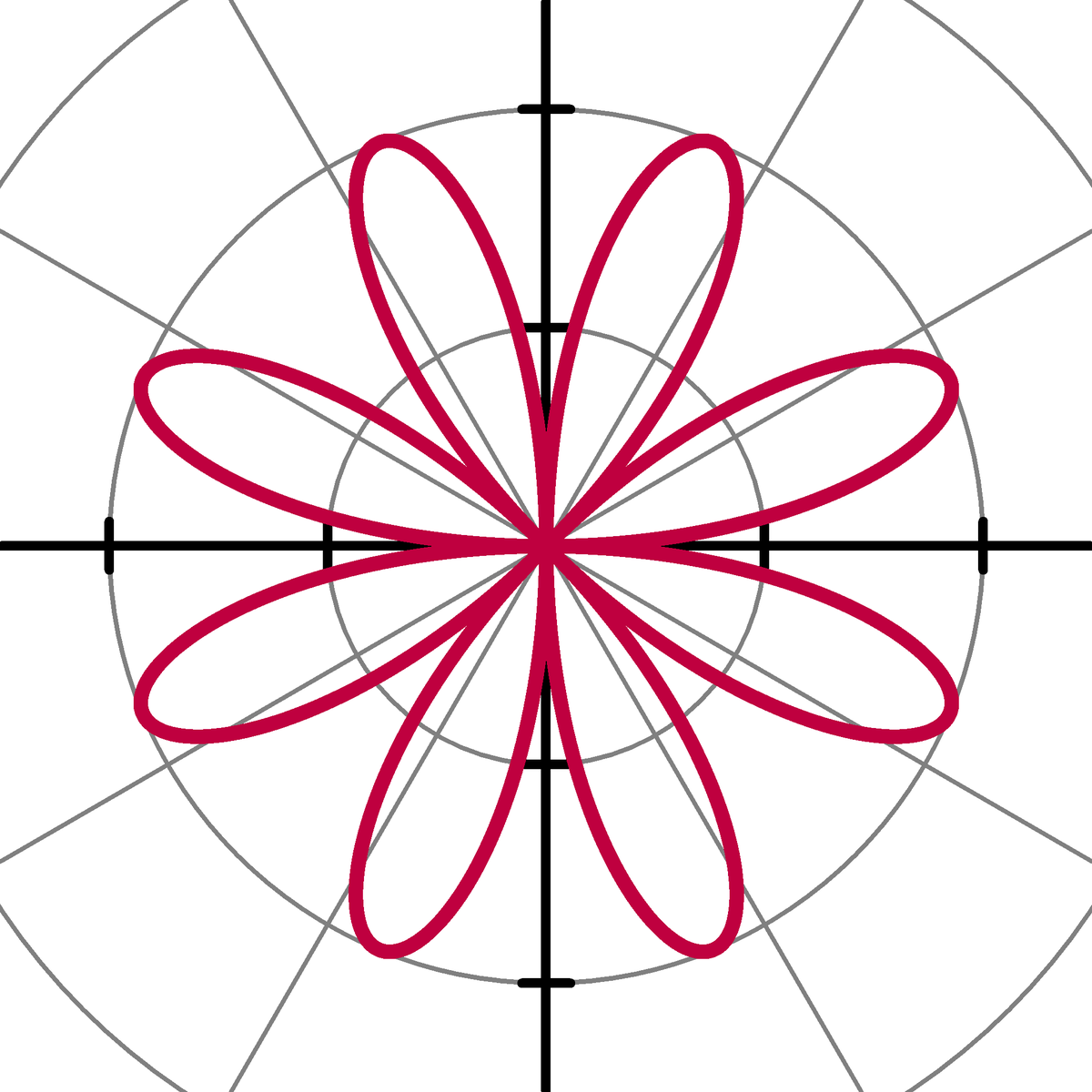
Rosace

Une rose polaire d'équation r(θ) = 2 sin 4θ

Une rosace est une courbe très connue qui ressemble à des pétales de fleurs, et qui peut être exprimée par une simple équation polaire :

r (θ) = a cos(k θ + φ 0)

Pour n'importe quelle constante réelle φ. Si k est un entier, cette équation produit une fleur avec 2k pétale(s) si k est pair, et k pétale(s ) si k est impair. Si k est un nombre rationnel, l'équation produit une courbe en forme de fleur dont les pétales se chevauchent. Ces équations ne peuvent fournir de courbe en forme de fleur à 2, 6, 10, 14,... pétales. La constante réelle a détermine la longueur d'un pétale du centre à son extrémité.

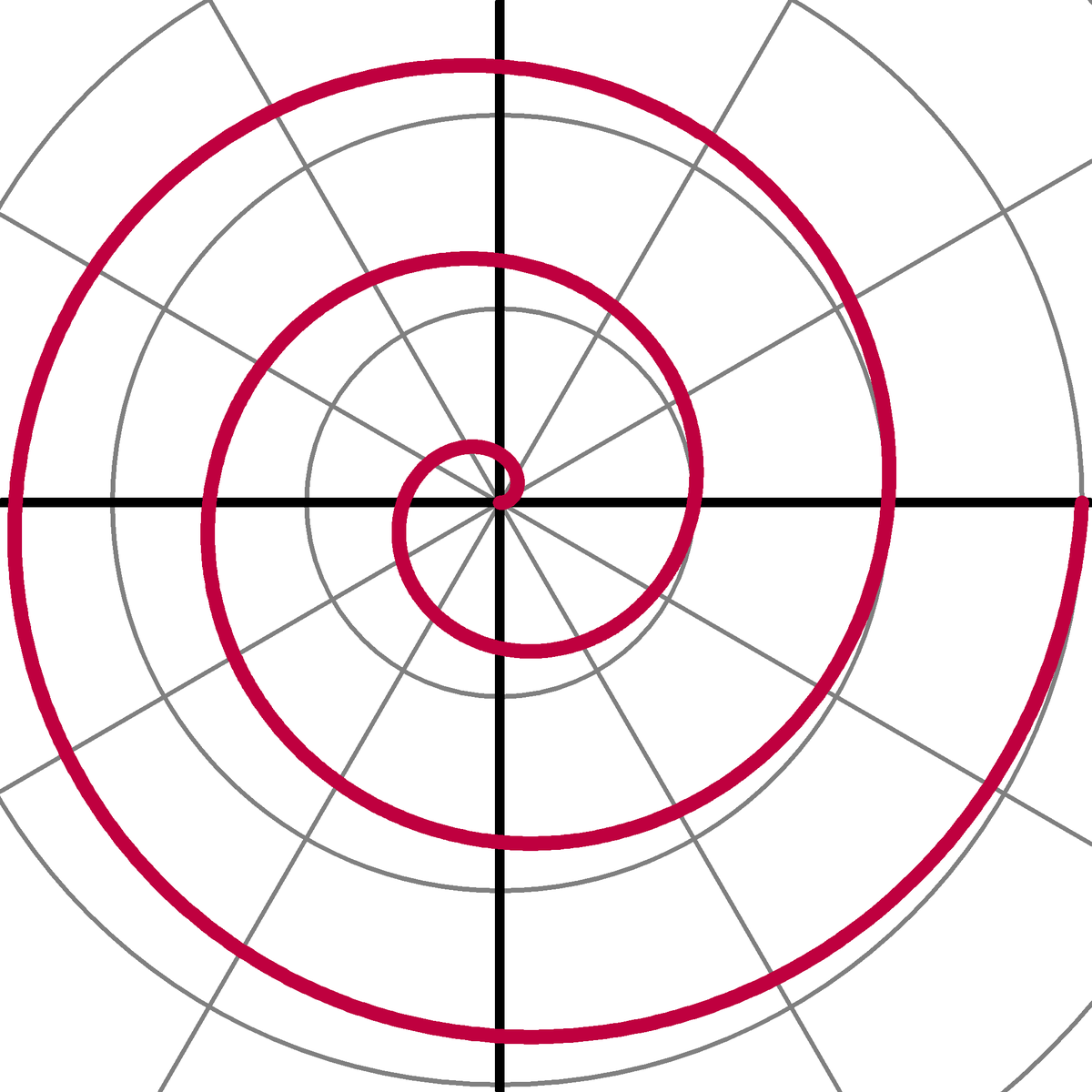
Spirale d'Archimède

Un bras d'une spirale d'Archimède d'équation r(θ) = θ pour 0 < θ< 6π

La spirale d'Archimède est une spirale célèbre découverte par Archimède, qui peut être également exprimée à partir d'une équation polaire simple :

r (θ) = a + b θ

Changer le paramètre a tourne la spirale, alors que b détermine la distance entre les bras, qui pour une spirale donnée est constante. Une spirale d'Archimède possède deux bras, l'un pour θ > 0 et l'autre pour θ < 0. Les deux bras sont connectés au pôle. Chaque bras est le symétrique de l'autre par rapport à l'axe vertical (90°/270°). Cette courbe est l'une des premières courbe, après les coniques, à être décrite par des termes mathématiques ; et à être un exemple de courbe simplement exprimée dans le système des coordonnées polaires.

Conique

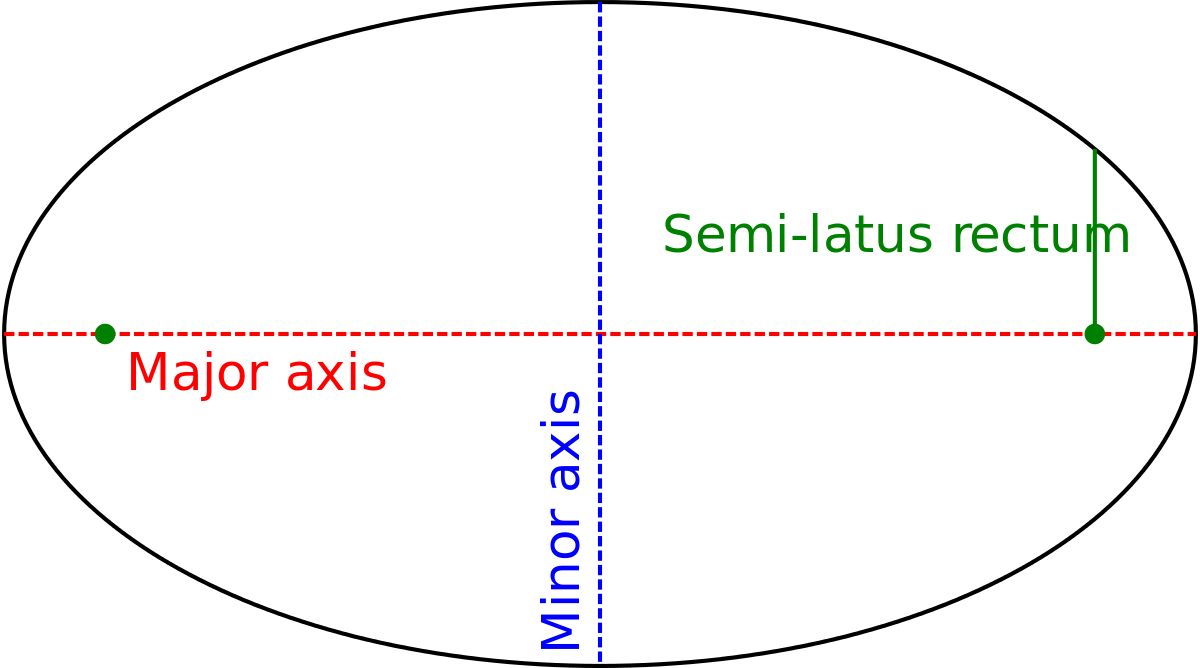
Une ellipse, et son paramètre

Une conique avec un foyer confondu avec le pôle et un autre sur l'axe polaire (0°), le grand axe étant confondu avec l'axe polaire) est donnée par l'équation :

$r(\theta) = \frac{p}{1 - e \cos \theta}$

où e est l'excentricité et p est appelé paramètre de la conique, et correspond à la longueur du segment perpendiculaire au grand axe joignant le foyer à la courbe. Si e > 1 l'équation définit une hyperbole, si e = 1, une parabole, si e < 1 une ellipse. Enfin pour e = 0 on obtient un cercle de rayon p.