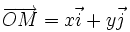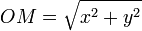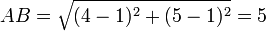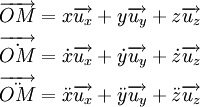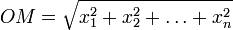Coordonnées cartésiennes - Définition

Coordonnées cartésiennes dans le plan

Dans un plan affine, les coordonnées cartésiennes sont sans doute la manière la plus naturelle de définir un système de coordonnées. Un repère (cartésien) du plan affine P est la donnée conjointe de :

• un point d'origine O.
• deux vecteurs i et j non colinéaires du plan vectoriel directeur .

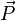
Les axes de coordonnées sont les droites affines et . Ces droites admettent des graduations respectives fournies par O et les vecteurs i et j.

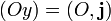
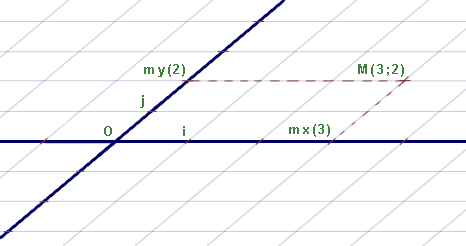
Par un point M, on est en droit de tracer :

• une droite parallèle à (Oy) qui coupe (Ox) en m_x d'abscisse x,
• une droite parallèle à (Ox) qui coupe (Oy) en m_y d'abscisse y.

Le couple de réels ( x , y ) est uniquement déterminé par le point M, on l'appelle les coordonnées de M dans le repère (O,i,j) ;

• Le réel x est appelé l'abscisse de M.
• Le réel y est appelé l'ordonnée de M.

Réciproquement, à tout couple (x,y), correspond un unique point M de coordonnées d'abscisse x et d'ordonnée y. C'est le point d'intersection :

• De la droite parallèle à (Ox) passant par le point de (Oy) d'abscisse y et
• De la droite parallèle à (Oy) passant par le point de (Ox) d'abscisse x et

Cette construction peut être interprétée comme la mise en place d'un parallélogramme de sommets O et M.

En termes vectoriels, on obtient l'identité suivante :

Ce qui permet de faire une correspondance entre le calcul sur des coordonnées et le calcul vectoriel.

Cas du repère orthonormé

Les repères orthonormés n'ont de sens que dans les plans affines euclidiens. Dans un plan affine euclidien , un repère (O,i,j) est dit orthonormé lorsque les vecteurs i et j sont d'une part de longueur 1 (de norme 1) et d'autre part orthogonaux , c'est-à-dire que le produit scalaire des deux vecteurs est nul.

Autrement dit, les axes de coordonnées sont deux droites affines orthogonales avec le même système de graduation.

Dans ce cas, on peut calculer des distances et des orthogonalités en utilisant le théorème de Pythagore. Voici un formulaire :

• Pour un point M d'abscisse (x,y), la distance OM s'écrit :

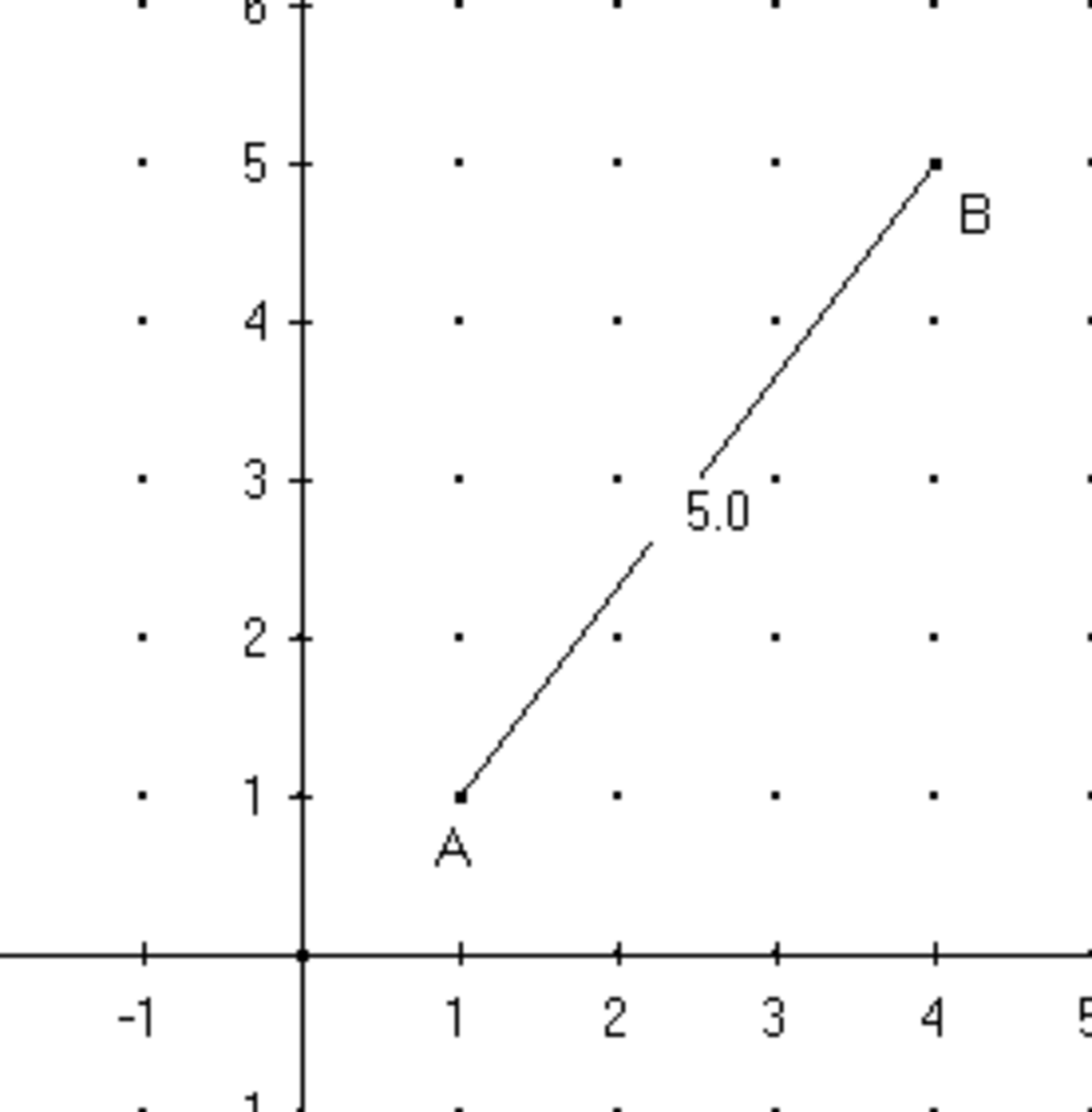
Dans le dessin ci-à droite, on a placé dans un repère orthonormé les points A de coordonnées (1,1) et B de coordonnées (4,5). Le calcul de la distance AB est alors :

• Les vecteur u( x , y ) et v( X , Y ) sont orthogonaux si et seulement si xX + yY = 0.

Le calcul des distances et des angles étant souvent un objectif de la géométrie plane euclidienne, on privilégie particulièrement les repères orthonormés. À tel point que certains ouvrages réservent le terme de coordonnées cartésiennes à ce type de repère, les autres coordonnées étant appelées coordonnées obliques.

Cinématique

Les quantités cinématiques, position, vitesse et accélération sont données par :

Coordonnées cartésiennes en dimension n

Les observations précédentes permettent de remarquer un lien entre couple ou triplet de réels et vecteurs du plan ou de l'espace. Ce lien se généralise à tout espace vectoriel ou affine de dimension finie sur un corps K.

Si est une base d'un espace vectoriel sur un corps K alors, pour tout vecteur , il existe un unique n-uplet élément de Kⁿ  tel que :

.

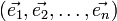
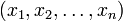
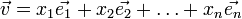
Ce n-uplet est appelé système de cordonnées cartésiennes du vecteur dans la base ). La correspondance entre chaque vecteur et chaque n-uplet permet de construire un isomorphisme d'espace vectoriel entre V et Kⁿ.

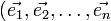
Pour travailler sur des systèmes de coordonnées de points, il suffit d'ajouter à la base précédente un point O appelé origine. Les coordonnées du point M étant celles du vecteur .

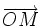
Enfin, pour travailler sur des distances, il sera nécessaire de construire une base orthonormale (dans laquelle tous les vecteurs sont de norme 1 et chaque vecteur est orthogonal à tous les autres) . La distance OM s'exprimera alors sous la forme suivante: