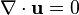Convection - Définition

Principe physique

Une particule de fluide chauffée à la base devient plus légère du fait de sa dilatation thermique et remonte sous l'action de la poussée d'Archimède. Arrivée au sommet de la couche, le fluide échange sa chaleur, se refroidit et s'alourdit. Il redescend alors et crée un transfert retour de chaleur. La première approche physique a été mise en place par Henri Bénard, avec l'étude de la convection dans une couche de fluide soumise à un gradient de température vertical. Ces expériences sont connues sous le nom de cellules de Bénard.

La convection de Rayleigh-Bénard

C'est le cas d'école étudié par Henri Bénard et Lord Rayleigh. On considère ici un système simple et on suppose un fluide newtonien, incompressible, dans l'approximation de Boussinesq, c'est-à-dire que la seule propriété physique qui change est la masse volumique.

Équations de conservation en jeu :

• Conservation de la masse :  ;
• Conservation de la quantité de mouvement ;
• Conservation de l'énergie.

Démarrage de la convection

Le transfert thermique dans une couche de fluide horizontale s'effectue par la conduction thermique et le mouvement du fluide. Quand on commence à imposer un gradient thermique entre les surfaces de la couche, un gradient thermique s'installe. Expérimentalement, on observe qu'au bout d'un certain temps, le fluide se met en mouvement spontanément : c'est le démarrage de la convection. Celui-ci est contrôlé par un nombre sans dimension appelé nombre de Rayleigh :

avec ρ la masse volumique, g la force de gravité, α le coefficient d'expansion thermique, ΔT la différence de température entre le haut et le bas de la couche, κ la diffusivité thermique et η la viscosité dynamique caractéristique (à noter : ces valeurs peuvent être variables dans le fluide et il est important de vérifier que l'on utilise bien des grandeurs caractéristiques)
Le démarrage s'effectue pour un nombre de Rayleigh de 657,5 pour des surfaces libres et 1770 pour les surfaces rigides.

Expression du flux de chaleur en convection (Loi de Newton)

Pour un écoulement à une température autour d'une structure à une température uniforme T_S de surface S, l'expression du flux de chaleur en convection est la suivante :

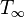
où h est le coefficient de transfert thermique.

Résolution du problème

L'analyse dimensionnelle permet de montrer que, en convection forcée, le nombre de Nusselt (permettant de calculer h puis le flux thermique par la formule indiquée ci-dessus) s'exprime en fonction du nombre de Reynolds et du nombre de Prandtl.

• , Nusselt local à une abscisse x

• , Nusselt moyen sur une longueur L

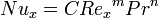
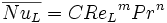
où C, m et n dépendent des caractéristiques du fluide, de la géométrie et du régime d'écoulement.

L'ingénieur dispose alors d'une série de formules empiriques établies sur des configurations typiques (plaque plane, écoulement autour d'un cylindre ...) afin d'en déduire le coefficient de transfert thermique.