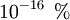Contraction des longueurs - Définition

En relativité générale

Un cercle en rotation

Ayant élaboré le principe d'équivalence qui permet de comprendre qu'une accélération et la gravitation sont localement indicernables, Einstein a montré que la gravitation impliquait une contraction des mesures à l'aide de l'expérience par la pensée suivante :

Imaginons dans un référentiel inertiel K dans lequel un cercle est mis en rotation à vitesse angulaire constante autour de son centre, auquel est lié un référentiel en rotation K', donc non-inertiel. Un observateur sur le bord de ce cercle, et entrainé avec lui, subit une force centrifuge constante, qui, étant une accélération, est parfaitement assimilable à une force gravitationnelle constante dirigée vers l'extérieur du cercle.

Supposons qu'un observateur dans le référentiel tournant mesure un petit élément du périmètre non tournant. Si on ne connait que la relativité restreinte, on ne sait rien des mesures que doit constater l'observateur tournant (son référentiel n'étant pas inertiel), par contre on sait ce que doit observer l'observateur inertiel : celui-ci observe que l'unité de mesure utilisée par l'observateur tournant est contractée car supposée petite par rapport au périmètre du cercle et donc quasi-parallèle à la vitesse qui est tangente au cercle. Donc l'observateur tournant doit constater que la mesure du périmètre immobile est supérieure à celle faite quand son référentiel ne tournait pas. Ainsi, la gravitation (ou tout phénomène équivalent) donne une contraction des mesures de longueurs par rapport aux mesures faites dans les référentiels inertiels.

Cette expérience par la pensée permet d'obtenir plus d'informations :

Si l'observateur tournant mesure un petit élément du rayon du cercle, il constatera que cette mesure est égale à celle du cercle immobile : cet élément du rayon est une longueur perpendiculaire à la direction du mouvement, qui est tangente au cercle, donc l'observateur inertiel n'y verra aucune contraction de l'unité de mesure quand elle lui est alignée. A priori, en tournant sur lui-même, le cercle reste un cercle. Pourtant, par les mesures faites qu'il a faites, l'observateur tournant a  : à ses yeux, le cercle en rotation ne vérifie pas , propriété qui est toujours vraie dans le cadre d'un espace euclidien. Ainsi, la gravitation (ou tout phénomène équivalent) oblige l'observateur qui la subit à utiliser un espace non euclidien, un espace courbé.

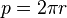
On remarquera qu'à partir d'un certain rayon, le bord du cercle est supposé aller à la vitesse de la lumière, ou même à une vitesse supérieure : ces résultats soulignent l'impossibilité matérielle de réaliser des référentiels tournant ayant de grandes dimensions.

Dans cette expérience par la pensée, il faut se garder de voir autre chose que des indices de la théorie relativiste de la gravitation : la force centrifuge est assimilable que localement à une force gravitationnelle, qui d'ailleurs est particulière du fait, par exemple, que seules sont contractées les longueurs parallèles à la vitesse de rotation et pas celles qui sont perpendiculaires au plan du cercle.

Considérations générales

En relativité générale, la présence d'un champ de gravitation est une déformation de l'espace-temps et ce qui concrètement s'approche le plus de la ligne droite est une géodésique de rayon lumineux qui n'est pas droite si on la compare à un référentiel euclidien fictif : ainsi observe-t'on une déviation de la lumière émise par les étoiles lors du passage à proximité de leur trajectoire d'une masse telle que le soleil. À tel point que l'on observe des lentilles gravitationnelles montrant ainsi que dans cette théorie deux lignes droites peuvent partir d'un même point et se croiser plus loin.

Ainsi, toutes les distances et toutes les formes sont-elles modifiées par la présence d'une masse : par exemple, une règle droite réelle suit en fait une géodésique de rayon lumineux, la distance entre ses extrémités varie aux yeux d'un observateur éloigné du champ de gravitation, sa forme ne lui semble pas correcte pour faire des mesures de distance et est même variable en fonction de sa direction par rapport au champ de gravitation (la déformation de l'espace).

La détection des ondes gravitationnelles se base sur la mesure d'une variation d'une longueur de l'ordre de lors de leur passage.